Umk_Oed

Система (2.3) имеет трехдиагональную матрицу. Эта система может быть решена методом прогонки или Гаусса. Метод прогонк и рассматривается в пункте 6.7.2 учебного пособия.

После решения системы коэффициенты сплайна di, bi определим через коэффициенты сi с помощью явных формул

Существуют специальные виды записи сплайнов на каждом из промежутков [xi ,xi + 1 ] [9], которые позволяют уменьшить число неизвестных коэффициентов сплайна. Вводятся обозначения

Кубический сплайн, записанный в таком виде, на каждом из промежутков [xi ,xi + 1 ] непрерывен вместе со своей первой производной на [a,b].

Выберем mi таким образом, чтобы и вторая производная была непрерывна во всех внутренних узлах. Отсюда получим систему уравнений:

В результате получаем аналогичную систему с трехдиагональной матрицей. Решаем систему линейных уравнений относительно коэффициентов mi методом пргонки.

2.2. Сходимость процесса интерполирования кубическими сплайнами

Доказывается, что при неограниченном увеличении числа узлов на одном и том же отрезке [ a,b] S(x) f (x) . Оценка погрешности

интерполяции R(x) f (x) S(x) зависит от выбора сетки и степени

гладкости функции f(x). При равномерной сетке

xi a i h (i=0,1,…,n)

Другие постановки задачи интерполирования функций.

1. Если функция периодическая, то используется тригонометрическая интерполяция с периодом l, которая строится с помощью тригонометрического многочлена

коэффициенты которого находятся из системы уравнений

Tn (xi ) f (xi ) (i= 1,2,…, 2n+1).

2. Выделяют приближение функций рациональными, дробно – рациональными и другими функциями. В данном пособии эти вопросы не рассматриваются.

2.4 Аппроксимация функций методом наименьших квадратов

К такой задаче приходят при статистической обработке экспериментальных данных с помощью регрессионного анализа. Пусть

некоторой величины у.

Требуется подобрать вид аппроксимирующей зависимости y=f(x), связывающей переменные х и у. Здесь могут иметь место следующие случаи. Во-первых: значения функции f(x) могут быть заданы в достаточно большом количестве узлов; во-вторых: значения таблично заданной функции отягощены погрешностями. Тогда проводить приближения функции с помощью интерполяционного многочлена нецелесообразно, т.к.

- число узлов велико и пришлось бы строить несколько интерполяционных многочленов;

- построив интерполяционные многочлены, мы повторили бы те же самые ошибки, которые присущи таблице.

Будем искать приближающую функцию из следующих соображений:

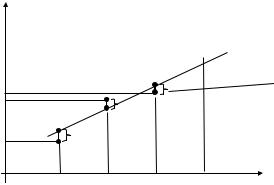
1)приближающая функция не проходит через узлы таблицы и не повторяет ошибки табличной функции;

2)чтобы сумма квадратов отклонений приближающей функции от таблично заданной в узлах таблицы была минимальной.

у

уn

yn-1 отклонения y1

y0

Рисунок 6 – Графическое изображение отклонений приближающей функции от таблично заданной

Рассмотрим линейную задачу наименьших квадратов. Определение. Уровень погрешности, допускаемый при снятии

характеристики измеряемой величины, называется шумом таблицы. Пусть функция y=f(x) задана таблицей приближенных значений

yi f(xi ), i=0,1,…,n, полученных с ошибками i yi0 yi , где yi0 f (xi) . Пусть даны функции 0( x ), 1( x ),..., m( x ), назовем их базисными

функциями.

Будем искать приближающую (аппроксимирующую) функцию в виде линейной комбинации базисных функций

Такая аппроксимация называется линейной, а Фm (х) – обобщенным многочленом.

Будем определять коэффициенты обобщенного многочлена c0 ,…,cm используя критерий метода наименьших квадратов. Согласно этому критерию вычислим сумму квадратов отклонений таблично заданной функции от искомого многочлена в узлах:

В случае, когда m=n мы получим интерполяционный многочлен, поэтому выберем m<<n. Так же необходимо задать числа ε1 и ε2 , учитывая следующее:

1) 1 >0 и 2 >0 должны быть такими, чтобы m находилось между ними;

2)первоначально m выбирают произвольно, но учитывая условие, что m<<n;

3)выбрав m, строят системы (2.13) и (2 .13a), решив которые, находят c0 ,…, cm ;

4)используя найденные коэффициенты, вычисляется m и

проверяется, попало ли оно в промежуток между 1 и 2 . Если попало, то степень многочлена выбрана правильно, иначе

а) если m > 1 , то степень необходимо уменьшить хотя бы на единицу;

б) если m < 2 , то степень необходимо увеличить хотя бы на

единицу.

5) затем строим приближающую функцию .

Очень часто для приближения по методу наименьших квадратов используются алгебраические многочлены степени m n, т.е. k ( x ) x k . Тогда нормальная система (2 .13) принимает следующий вид:

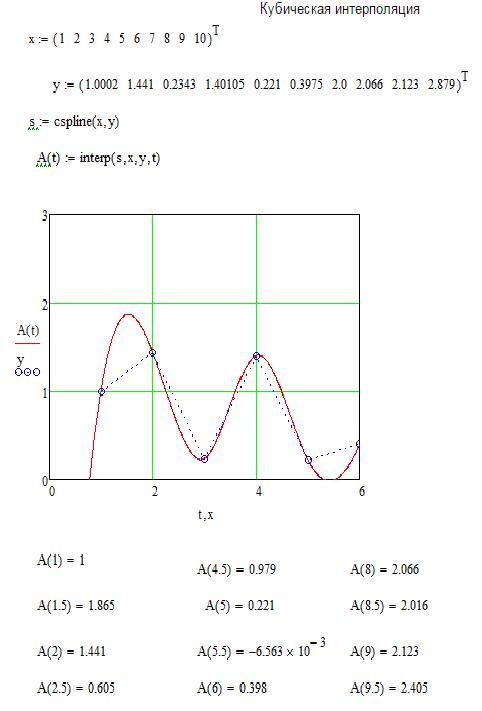
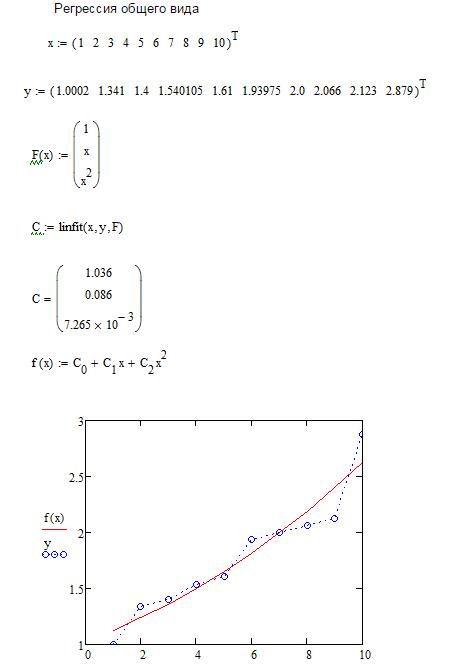
Задание №1 на самостоятельную работу. Для данных, приведенных в таблице: 1) выполнить интерполяцию сплайном 3 -го порядка; 2) выполнить аппроксимацию данных по методу наименьших квадрат ов с подбором аппроксимирующей функции.

Пример выполнения заданий приведен ниже.

Лекции 3, 4. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ Основные задачи математической статистики

Математические законы теории вероятностей не являются лишь абстрактными, лишенными физического содержания. Они представляют собой математическое выражение реальных закономерностей в массовых случайных явлениях природы. В основе таких понятий, как события и их вероятности, случайные величины, их законы распределения и числовые характеристики лежит опыт; каждое исследование случайных явлений методами теории вероятностей опирается на экспериментальные опытные данные или систему наблюдений.

Разработка методов регистрации, описания и анализа

статистических (экспериментальных) данных, получаемых в результате наблюдения массовых случайных явлений и составляет предмет науки

–математической статистики.

Взависимости от характера решаемого практического вопроса и от объема экспериментального материала задачи математической

статистики можно разделить на типичные.

1. Задача определения закона распределения случайной величины по статистическим данным.

На практике нам всегда приходится иметь дело с ограниченным количеством экспериментальных данных, в связи с этим результаты наблюдений и их обработки всегда содержат больший или меньший элемент случайности. При этом важно уметь выделить как постоянные и устойчивые признаки явления, так и случайные, проявляющиеся в данной серии наблюдений только за счет ограниченного объема экспериментальных данных. В связи с этим возникает характерная задача группировки, сглаживания или выравнивания статистических данных, представления их в компактном виде с помощью аналитических зависимостей.

2. Задача проверки правдоподобия гипотез.

Статистические данные могут с большим или меньшим правдоподобием подтверждать или не подтверждать справедливость той или иной статистической гипотезы. Например, ставится такой вопрос: согласуются или нет данные эксперимента с гипотезой о том, что данная случайная величин а или признак подчинены тому или иному закону распределения? Другой подобный вопрос: указывают ли данные наблюдений на наличие объективной зависимости случайной величины от одной или нескольких случайных величин? Для решения подобных вопросов существуют ме тоды проверки статистических гипотез с помощью критериев согласия.

3. Задача определения неизвестных параметров распределения.

Часто при обработке статистических данных нет необходимости определения законов распределения исследуемых случайных величин

(признаков). Или же характер закона распределения известен заранее (до опыта). Тогда возникает более узкая задача обработки данных – определить только некоторые числовые характеристики случайной величины, оценить их точность и надежность.

Таким образом, здесь перечислены только те задачи математической статистики, которые наиболее важны по своим практическим применениям.

3.2 Статистическая совокупность и статистическая функция распределения

Предположим, что изучается некоторая случайная величина Х, закон распределения которой неизвестен и требуется определить этот закон по данным наблюдений (опытным данным). Совокупность наблюдений Х1 , Х2 , …, Хn и представляет собой статистическую совокупность. Иногда говорят, что получена выборка объема n. При большом n весь диапазон значений Хi делят на k интервалов (разрядов) и подсчитывают количество значений mi , приходящихся на i-й интервал.

Это число делят на общее число наблюдений n и получают частоту, соответствующую данному интервалу: pi mi / n. Для контроля: сумма

частот всех интервалов равна единице. Тем самым значения Хi будут отсортированы в порядке возрастания. Таблица с указанием разрядов и соответствующих им частот значений Хi называется статистическим рядом. Таким образом, мы получаем сгруппированные данные.

Определение. Статистической функцией распределения

случайной величины Х называется частота события Х<х в данной статистической совокупности:

Fn (x)=p *(X<x).

Для того, чтобы найти значение статистической ф ункции распределения при данном х, достаточно подсчитать число опытов, в которых величина Х приняла значение меньше х, и разделить на общее число n произведенных опытов. Статистическая функция распределения любой случайной величины (дискретной или непрерыв ной) представляет собой ступенчатую функцию, скачки которой соответствуют наблюденным значениям случайной величины и по величине равны частотам этих значений. Но при больших значениях n (когда сотни скачков), построение функции Fn (x) трудоемко и себя не оправдывает. Другой способ построения Fn (x) будет рассмотрен ниже.

При увеличении числа опытов n, согласно теореме Бернулли, частота события сходится по вероятности к вероятности этого события. Следовательно, при увеличении n статистическая функция распределения Fn (x) сходится по вероятности к подлинной функции распределения F(x) случайной величины Х. По сути самого определения