Umk_Oed

n

X (n) ( X i ) / n .

i 1

Найдем его математическое ожидание

n

M ( X (n)) ( mx ) / n mx .

i 1

Отсюда следует, что X (n) является несмещенной оценкой для

математического ожидания mx .

При рассмотрении закона больших чисел мы убедились, что при увеличении n величина X (n) сходится по вероятности к mx . Тогда эта

оценка является и состоятельной. Определим теперь дисперсию этой оценки:

n

D( X (n)) D( X i ) / n2 Dx / n .

i 1

Эффективность или неэффективность оценки зависит от вида распределения величины Х. Например, доказано, что если величина Х

есть среднее арифметическое n значений случайной величины X2 и она сходится по вероятности к М(Х2 ). Второе слагаемое сходится по

вероятности к mx2 . Тогда дисперсия DX (n) сходится по вероятности к

M ( X 2 ) mx2 Dx , т.е. оценка DX (n) является состоятельной.

Проверим, является ли оценка DX (n) также и несмещенной. Для этого раскроем выражение (3.15):

Найдем математическое ожидание величины (3 .16):

Последнее соотношение следует понимать так: вероятность того, что

интервалом.

Замечание. Ранее мы неоднократно рассматривали вероятность попадания случайной величины X в заданный (неслучайный) интервал.

Здесь же параметр θ не случайная величина, а случайна величина ˆ и

θ

следовательно, случайны границы доверительного интервала. Поэтому

этот интервал накроет точку θ.

Перейдем к вопросу о нахождении границ доверительного интервала. Для этого рассмотрим задачу о доверительном интервале для математического ожидания.

Предположим, что X1 , X2 , …, Xn являются независимыми и одинаково распределенными случайными величинами с математическим ожиданием m и конечной дисперсий σ 2 , которые неизвестны. Для этих параметров получены оценки:

предельной теореме, при достаточно большом n закон распределения X (n) близок к нормальному. Характеристики этого закона –

математическое ожидание и дисперсия равны соответственно m и σ2 /n (п.3.3). Тогда польз уясь известной формулой (см. п.3 .4.)

Р(|X−m|<δ)=2Φ0 (δ/σ) и заменив в ней Х на X (n) , σ2 на S2 (n)/n, получим

P(| X (n) m | δ) 2Φ0 (δn / S 2 (n)) 2Φ0 (tγ ) ,

где tγ δ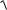n / S 2 (n) .

Тогда δ tγ S 2 (n) / n и можем записать

P(| X (n) m | tγ S 2 (n) / n ) 2Φ0 (tγ ) .

Приняв во внимание, что эта вероятность задана и равна γ, а также найдя значение tγ из равенства Φ0 (tγ )=γ/2 по таблице интеграла Лапласа, можем теперь записать окончательную формулу доверительного интервала для неизвестного математического ожидания:

Требуется найти оценку mˆ для математического ожидания m величины X и построить 90-процентный доверительный интервал для m.

Решение. Определим среднее арифметическое

Лапласа находим t0 , 9 0 =1,643. Отсюда доверительный интервал:

10,69<m<10,87.

Пример 3.9. Построим 90 − процентный доверительный интервал для среднего значения m статистической совокуп ности из примера 3 .1. Из п.3.4 имеем следующие оценки X (199) 0,351, S2 (199)=0,081. Отсюда

значения множителя 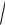S 2 (199) / n 0,020 . По таблице интеграла Лапласа

t =1,643. Отсюда доверительный интервал: 0,318< m<0,384. Доверительный интервал, определенный формулой (3 .18) является

лишь приближенным. Это видно по выкладкам, которые были проделаны при выводе этой формулы. Теперь запишем точное выражение 100∙γ − процентного доверительного интервала для неизвестного математического ожидания m.

Пусть X1 , X2 , …, Xn являются нормально распределенными

распределение Стьюдента с n−1 степенями свободы. Плотность этого

В этом случае также говорят, что случайная величина T имеет t – распределение с n−1 степенями свободы.

Точный (для любого n≥2) 100∙γ – процентный доверительный интервал для m определяется как

степенями свободы определяется из условия

tn 1, γ

2 Sn 1 (t) dt γ .

0

Таким образом, при выводе формулы (2 .19) использована случайная величина T.

Таблица значений критических точек tn 1,γ приведена в приложении

(табл.5).

Пример 3.10. Построить 90%-й доверительный интервал для m по данным примера 3 .8. Ранее были определены оценки: X (20) 10,78 , S2 (20)=0,064, а также величина

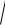S 2 (20) / 20 0,0565.

По таблице значений tn 1, γ находим значение t1 9 ; 0 , 9 =1,729. Тогда 90%-й

доверительный интервал будет 10,68< m<10,88.

Таким образом, доверительный интервал, определяе мый формулой (3.19) шире, чем (3.18). Этот факт иллюстрирует и рис. 3.13, где приведены графики плотности t − распределения с 4 -мя степенями свободы и стандартного нормального распределения.

Рис.3.13

Кривая t − распределения меньше поднимается вверх и имеет боле е длинные хвосты, чем кривая нормального распределения и поэтому для

любого конечного n справедливо неравенство tn 1, γ tγ . В тех случаях,

когда n довольно небольшое число, разница между (3.18) и (3.19) будет ощутимой.

Выше мы рассматривали задачу построения доверительного интервала для неизвестного математического ожидания. Точно также

определяется доверительный интервал для дисперсии D. Только при его получении используется случайная величина U=(n−1)S2 (n)/D, которая имеет распределение χ 2 с n−1 степенями свободы (см.п.2 .5). Выразим

случайную величину – оценку S2 (n) через U: S 2 (n) U D . Зная закон n 1

распределения величины U, можно найти для нее доверительный интервал с надежностью γ. Доверительный интервал построим таким образом, чтобы вероятности выхода величины U за пределы интервала вправо и влево (заштрихованные площа ди на рис.3.14) были одинаковы и равны

1 .

2 2

Воспользуемся таблицей значений χ 2кр (α, r) для случая r=n−1 и в

соответствующей строке найдем два значения χ 2 : одно, отвечающее вероятности α1 =α/2; другое – вероятности α2 =1−(α/2). Обозначим эти

значения χ12 и χ22 , причем χ12 будет правым концом доверительного интервала, а χ22 −левым.

fr(U)

доверительный интервал

Рис. 3.14

Таким образом, построим доверительный интервал для дисперсии с границами D1 и D2 , который накрывает точку D с вероятностью γ:

P(D1 D D2 ) γ .

Потребуем также одновременного выполнения условия

является 100∙γ − процентным доверительным интервалом для неизвестной дисперсии.

Пример 3.11. Найти 90%-й доверительный интервал дл я дисперсии в условиях примера 3 .8, если известно, что величина Х распределена нормально.

Решение. Имеем γ=0,9; α=0,1; α/2=0,05. По таблице значений χ 2 (α,r) при r=n−1=19 находим

для α1 α2 0,05: χ12 30,1; для α2 1 α2 0,95: χ22 10,11.

Учитывая, что S2 (20)=0,064, используя формулу (3 .20), получим 90%-й доверительный интервал для дисперсии: 0,04< D<0,12.

3.9 Связь между доверительным интервалом и проверкой гипотез о среднем значении

В п.8.8 были даны два вида доверительных интервалов для неизвестного среднего значения m величины X; формула (3.18) − для приближенного доверительного ин тервала; а формула (3 .19) − для точного. Более правильной будет следующая интерпретац ия доверительного интервала.Если будет построено большое количество независимых 100∙γ – процентных доверительных интервалов, каждый из которых основывается на n разных наблюдениях, где n − достаточно большое число, то доля интервалов, которые содержат ( покрывают) m, будет равна γ. Эта доля и называется покрытием для доверительного интервала.

На покрытие доверительного интервала (3 .19) оказывает влияние вид распределения величин Xi . В таблице 3.7 представлена оценка покрытия для 90%-х доверительных интервалов, основанная на 500 независимых экспериментах, при разных объемах выборок n (5, 10, 20 и 40) и таких распределениях как: нормальное, экспоненциальное, «хи – квадрат» с одной степенью свободы, логнормальное ( ey , где Y - стандартная нормальная случайная величины), а также гиперэкспоненциальное, функция распределения которого

F(x) 0,9(1 e 2x ) 0,1(1 e 2x /11) .

Табл. 3.7

Например, значение 0,878 при n=10 для экспоненциального распределения получено следующим образом. Десять наблюдений сгенерировали по экспоненциальному распределению с известным средним значением m, а 90%-й доверительный интервал построили по выражению (3.19) и определили, содержит ли этот интервал среднее значение m (это один эксперимент). Затем всю процедуру повторили 500 раз, и доля интервалов, содержащих значение m, в 500-х доверительных интервалах составила 0,878.

Как следует из таблицы 3.7, для отдельного распределения покрытие становится ближе к 0,90 по мере возрастания n, что следует из центральной предельной теоремы. Кроме того, для конкретного n покрытие уменьшается по мере увеличения асимметрии. Следовательно, чем больше асимметрия у распределения, тем больший объем выборки необходим для получения удовлетворительного (близкого к 0,90) покрытия.

Далее рассмотрим следующую задачу. Допустим, что величины X1 , X2 ,…, Xn являются нормально распределенными (или приближенно нормально распределенными) и что следует проверить нулевую гипотезу Н0 , согласно которой m=m0 , где m0 - заданное гипотетическое

значение m. Интуитивно ясно, что если X (n) m0 является большой

величиной, то гипотеза Н0 не может быть истиной ( X (n) – точечная

несмещенная оценка m).

Воспользуемся статистикой (функцией величины Xi ), распределение

распределение с n−1 степенями свободы. Тогда «двусторонний» критерий проверки гипотезы Н0 : m=m0 при конкурирующей гипотезе Н1 : m≠m0 будет иметь следующую форму:

где tn − 1 , γ – критическая точка t – распределения.

Отрезок числовой оси, соответствующий опровержению Н0 , а именно: множество всех х, для которых |x|> tn − 1 , γ , называется критической областью критерия, а вероятность попадания статистики tn в критическую область при условии, что гипотеза Н0 является истиной, равна α и называется уровнем значимости критерия. Как правило, выбирается уровень α, равный 0,05 или 0,1 0. Критерий проверки гипотезы (3 .21) называется t – критерий, а критические

значения tn − 1 , γ мы уже использовали при построении довер ительных интервалов по формуле (3 .19).

При проверке гипотезы встречаются два вида ошибок.

1. Если отвергнуть гипотезу Н0 тогда как она верна, допускают ошибку первого рода. Вероятность ошибки первого рода равна уровню значимости α и, следовательно, находит ся под контролем исследователя.

2. Если же принимать гипотезу Н0 тогда, когда она ложна, допускают ошибку второго рода. Вероятность ошибки второго рода для заданного уровня α и объема выборки n обозначается β. Она зависит от того, что в действительности пр авильно (в сравнении с Н0 ), и может быть неизвестна.

Мощностью критерия называют величину δ=1−β. Она равна вероятности опровержения гипотезы Н0 , когда она ложна, а верна конкурирующая гипотеза. (Желательно, чтобы критерий имел высокую мощность).

При заданном α мощность критерия можно увеличить только путем увеличения числа опытов n и только так можно добиться уменьшения ошибок первого и второго рода.

Так как мощность критерия может быть невелика и неизвестна, далее, когда статистика tn не будет попадать в критическую область, будем считать, что гипотеза Н0 не опровергается (вместо « Н0 принимается»).

Когда Н0 не опровергается, часто точно неизвестно, правильна Н0 или ложна, поскольку критерию недостает мощности, чтобы обнаружить различия между нулевой гипотезой Н0 и тем, что в действительности правильно. В этом состоит главный недостаток критериев проверки гипотез.

Далее сравним критерий проверки гипотез (3.21) и доверительный

двустороннюю критическую область (3 .21) была равна уровню значимости α, следовательно, вероятность попадания критерия в область принятия гипотезы (− tn − 1 , γ , tn − 1 , γ ) равна 1−α=γ. Другими словами, с надежностью γ выполняется неравенство

tn 1,γ Х (n) m0 / 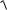S 2 (n) / n tn 1,γ ,

или равносильное неравенство

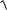
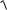
Х (n) tn 1,γ S 2 (n) / n m Х (n) tn 1,γ S 2 (n) / n .

Таким образом, мы получим доверительный интервал (3.19) для оценки неизвестного математического ожидания m нормального распределения с надежностью γ.

Замечание. Хотя построение доверительного интервала для m и двусторонней критической области для проверки гипотезы Н0 : m=m0 и