
Пособие по контрольным. Линейная алгебра
.pdfЛИНЕЙНАЯ АЛГЕБРА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ
Красноярск 2015
Составитель Т. И. Качаева, канд. физ.-мат. наук, кафедра высшей математики 1, ИМиФИ.
Предназначено для студентов – заочников экономического факультета.
@ Сибирский Федеральный Университет, 2015
2
КОНТРОЛЬНАЯ РАБОТА
1.Контрольная работа должна выполняться самостоятельно.
2.При решении задач нужно обосновывать каждый этап решения, исходя из теоретических положений курса.
3.Решение задачи должны доводиться до ответа.
4.Полученный ответ следует проверить способами, вытекающими из существа данной задачи.
5.Не следует применять формулы, которые не входят в программу курса.
6.Работа выполняется в отдельной тетради.
7.Условия задач должны быть переписаны полностью.
8.На обложке должны быть аккуратно записаны:
1)Фамилия, имя, отчество.
2)Курс, номер группы.
3)Номер варианта
4)Номер зачетной книжки.
9.Контрольная работа должна быть выполнена в срок (за 2 недели до сессии). В период сессии работы на проверку не принимаются.
10.Работа, выполненная не по своему варианту, не учитывается и назад не возвращается.
11.Студенты, не имеющие контрольной работы, к экзамену не допускаются.
3

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
ПРИМЕР 1. Выполнить действия в алгебраической форме. Результат записать в алгебраической, тригонометрической и показательной формах .
æ |
1+ i |
|
1- i ö |
|
z =10 ×ç |
2 - i |
+ |
|
÷ . |
|
||||
è |
|
4 + 2i ø |
||
РЕШЕНИЕ: Алгебраическая форма комплексного числа z: z = x + iy , x, y R , i − мнимая единица, причем i2 = -1. Выполним действия:
æ |
( |
1+ i |
) ( |
2 + i |
) |
|
( |
1 |
- i |
) ( |
4 |
- 2i |
) |
ö |
|
z =10 ×ç |
|
|
|
+ |
|
|
|
÷ |
= |
||||||
( |
2 - i) ( 2 + i) |
|
|
|
|
|
|
|
|||||||
è |
|
( 4 + 2i) ( 4 - 2i) ø |
|
||||||||||||
æ |
2 + 2i + i + i2 |
+ |
4 - 4i - 2i + 2i2 ö |
æ |
1+ 3i |
+ |
2 - 6i ö |
= |
6 + 6i |
= 3 |
+ 3i . |
||||
=10 × ç |
4 - i |
2 |
16 - 4i |
2 |
÷ |
=10 ×ç |
5 |
20 |
÷ |
2 |
|||||
è |
|
|
|
ø |
è |
|
ø |
|
|
|
|||||
z = 3 + 3i – результат в алгебраической форме. Тригонометрическая форма комплексного числа z:
z = r(cosϕ + sin ϕ) , где r = 
 x2 + y2 , j = arctg xy .
x2 + y2 , j = arctg xy .
Т.к. x = 3 > 0 и y = 3 > 0 , то число находится в 1-oй четверти.
r = |
|
= |
|
|
|
= 3 |
|
|
, j = arctg |
3 |
= arctg1= |
π |
(ϕ - угол в 1-ой четверти) |
|||
9 + 9 |
18 |
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
4 |
|
z = 3 + 3i = 3 |
|
|
|
æ |
p |
+ isin |
p ö |
|
|
|
|
|||||
2 |
|
|
|
|
||||||||||||
çcos |
4 |
÷ . |
|
|
|
|
||||||||||
|
|
|
|
|
|
è |
|
|
4 ø |
|
|
|
|
|||
Показательная форма комплексного числа: z = reij , поэтому 3 + 3i = 3 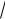 2ei×p4 .
2ei×p4 .
|
|
|
æ |
p |
|
p ö |
|
|
i×p |
|
Ответ: |
z = 3 + 3i = 3 2 |
+ isin |
= 3 |
|
||||||
çcos |
4 |
4 |
÷ |
2e 4 . |
||||||
|
|
|
è |
|
ø |
|
|
|
||
ПРИМЕР 2. Вычислить по формуле Муавра:
4

а) ( 
 3 - i)12 .
3 - i)12 .
РЕШЕНИЕ: Формула Муавра: zn = rn ( cosnj + sin nj)
Найдем тригонометрическую форму числа z = 
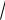 3 - i .
3 - i .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
-1 ö |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
r = |
|
|
|
|
|
3 |
|
|
|
|
+ |
-1 |
|
|
|
= |
2 , |
j = arctg ç |
|
|
|
÷ . |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
3 ø |
|
|
|||
Т.к. x = |
|
|
|
|
|
|
|
> 0 , y = −1< 0 , то число находится в 4-oй четверти, отсюда |
|||||||||||||||||||||||||
|
|
|
|
3 |
|||||||||||||||||||||||||||||
j = - |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
æ |
|
p ö |
|
æ |
|
p |
öö |
|
|
|
|
||
z = |
|
|
3 - i = 2 |
|
- |
|
- |
|
|
|
|
||||||||||||||||||||||
|
|
ç cos |
ç |
÷ |
+ isinç |
6 |
÷÷ |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
è |
|
6 ø |
|
è |
|
øø |
|
|
|
|
|||
z12 = ( |
|
|
|
|
|
- i)12 = 212 ×( cos( -2p) |
+ isin( -2p) ) = 212 . |
||||||||||||||||||||||||||
|
|
|
3 |
||||||||||||||||||||||||||||||
Ответ: ( |
|
|
|
|
|
|
- i)12 = 212 . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
б) 4 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
-625 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
РЕШЕНИЕ: Формула Муавра: |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
n |
|
|
= |
|
n |
|
|
æ |
|
|
|
|
j + 2pk |
+ isin |
j + 2pk ö |
|
|
||||||||||||||||
z |
|
r |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
ç cos |
n |
|
|
|
|
n |
|
÷ , где k = 0,n -1. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|||||||
Найдем тригонометрическую форму z = −625.
r = z = 625 , так как x > 0, y = 0 , то число находится на отрицательной части оси Х, т. е. ϕ = π . Итак, zсоs= -625i = 625( p + sin p) .
4 |
|
|
|
æ |
соs |
p + 2pk |
+ isin |
p + 2pk ö |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
k = 0,3 |
и количество корней равно |
||||||||||||||||||||||
|
-625 = 5ç |
|
|
4 |
|
|
|
|
4 |
|
|
÷ , где |
||||||||||||||
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|||||
4, все различные. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
æ |
|
|
p |
|
|
p ö |
|
|
|
5 |
|
|
(1 |
+ i) , |
|
|
|
|
|||
k = 0, |
|
z0 |
= 5ç cos |
4 |
+ isin |
÷ |
= |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
è |
|
|
|
|
4 ø |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
= 5 |
æ |
|
3p |
+ isin |
3p ö |
= |
|
|
5 |
|
( -1+ i) , |
|
|
|
|
|||||||
k = 1, |
z1 |
ç cos |
|
4 |
4 |
÷ |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
è |
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
æ |
|
|
|
5p |
|
|
|
5p |
ö |
|
|
5 |
|
|
( -1- i) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
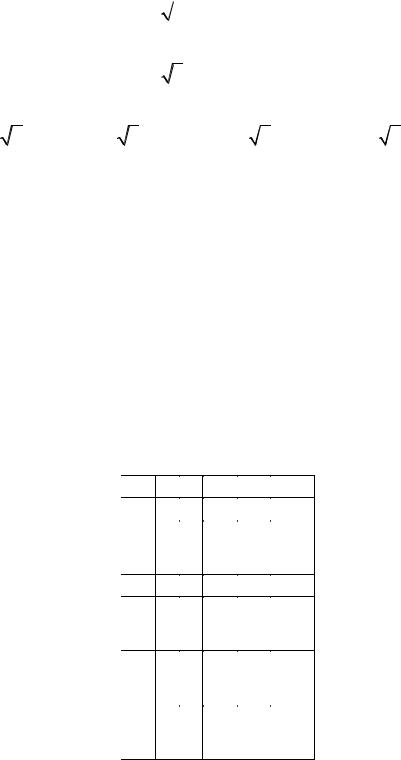
k = 2 , |
z2 |
|
= 5ç cos |
4 |
+ isin |
4 |
|
÷ |
= |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
= 5 |
æ |
|
|
|
7p |
+ isin |
7p |
ö |
= |
|
5 |
|
(1 |
- i) . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
k = 3, |
z3 |
|
ç cos |
4 |
4 |
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ответ: |
z |
|
|
= |
5 |
|
(1+ i) |
, |
z = |
5 |
|
|
( -1+ i) |
, |
z |
|
= |
|
5 |
|
( -1- i) |
, |
z = |
5 |
|
(1- i) |
. |
|||||||||||||||
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ПРИМЕР 3. Разложить многочлен на неприводимые множители в R и линейные множители в С, используя схему Горнера. Сделать проверку.
Р( х) = х4 + х3 - 3х2 + 3х -18.
РЕШЕНИЕ: Из основной теоремы алгебры следует, что многочлен четвертой степени имеет ровно четыре корня .Так как у многочлена с действительными коэффициентами корни являются делителями свободного члена, то делителями а0 = −18 являются числа: ±1,±2,±3,±6,±18 .
По схеме Горнера выясним, какие из них являются корнями многочлена
Р( х) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
−3 |
3 |
−18 |
|
1 |
1 |
2 |
−1 |
2 |
−16 |
|
− |
1 |
0 |
−3 |
6 |
−24 |
|
1 |
|
|
|
|
|
|
2 |
1 |
3 |
3 |
9 |
0 |
|
− |
1 |
1 |
1 |
7 |
|
|
2 |
|
|
|
|
|
|
3 |
1 |
6 |
19 |
6 |
|
|
|
|
|
|
4 |
|
|
− |
1 |
0 |
3 |
0 |
|
х = 1 не является корнем, |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
х = −1 не является корнем, |
|
|
|
|
|
|
х1 = 2 − корень, |
|
|
|
|
|
|
х = −2 не является корнем, |
|
|
|
|
|
|
х = 3 не является корнем, |
|
|
|
|
|
|
6

x2 = − 3 − корень.
Итак: х4 + х3 − 3х2 + 3х − 18= ( х − 2) ( х + 3) ( х2 + 3) − разложение в R.
х2 + 3 = 0, х3,4 = ±
 3i , отсюда
3i , отсюда
х4 + х3 − 3х2 + 3х −18 = ( х − 2) ( х + 3) ( х − 
 3i)( х +
3i)( х + 
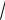 3i) − разложение в С.
3i) − разложение в С.
Проверка:
(х − 2) ( х + 3) ( х − 
 3i)( х +
3i)( х + 
 3i) = ( х2 + х − 6)( х2 + 3) =
3i) = ( х2 + х − 6)( х2 + 3) =
=х4 + 3х2 + х3 + 3х − 6х2 −18 = х4 + х3 − 3х2 + 3х −18.
ПРИМЕР 4. Используя свойства определителей, вычислить определитель:
1 |
2 |
3 |
4 |
−5 |
|
|
|||||
2 |
1 |
2 |
3 |
−1 |
|
3 |
2 |
1 |
2 |
−1 |
|
4 |
3 |
2 |
1 |
5 |
|
1 |
1 |
2 |
1 |
4 |
|
РЕШЕНИЕ: Для вычисления определителя надо в одной из строк (столбцов) получить нули на месте всех элементов, кроме одного. Будем использовать следующие свойства определителей:
1)перестановка строк и столбцов меняет знак определителя;
2)если умножить строку (столбец) на число и сложить с другой строкой (столбцом), то определитель не изменится;
3)из строки (столбца) можно вынести общий множитель k;
4)определитель равен сумме произведений элементов строки (столбца) на их алгебраические дополнения.
|
|
1 |
2 |
3 |
4 |
−5 |
|
|
|
|
|||||||
|
|
2 |
1 |
2 |
3 |
−1 |
|
|
= |
|
3 |
2 |
1 |
2 |
−1 |
|
Сделаем преобразования, чтобы получить нули в 5 |
|
|
4 |
3 |
2 |
1 |
5 |
|
|
|
|
1 |
1 |
2 |
1 |
4 |
|
|
столбце и раскроем определитель по 5 столбцу.
7
Складываем 3-ю строку со 2-ой строкой умноженной на ( -1) , записываем 3- ей строкой.
Складываем 4-ую строку с 1-ой, записываем 4-ой строкой.
5-ую строку складываем со 2-ой, умноженной на 4, записываем 5-ой строкой.
1-ую строку складываем со 2-ой умноженной на ( -5) и записываем 1-ой
строкой. Получаем: |
|
|
|
|
|
|
|
|||||
|
|
-9 |
-3 |
-7 |
-11 |
0 |
|
-9 |
-3 |
-7 |
-11 |
|
|
|
|
||||||||||
|
|
|
|
|||||||||
|
|
2 |
1 |
2 |
3 |
-1 |
|
|
||||
|
|
|
1 |
1 |
-1 |
-1 |
|
|||||
|
|
1 |
1 |
-1 |
-1 |
0 |
= |
Преобразуем, получая нули во |
||||
|
|
5 |
5 |
5 |
5 |
|||||||
|
|
5 |
5 |
5 |
5 |
0 |
|
9 |
5 |
10 |
13 |
|
|
|
9 |
5 |
10 |
13 |
0 |
|
|
||||
|
|
|
|
|
|
|
|
|||||
второй строке.
Складываем 4-ый столбец с 1-ым, записываем 1-ым столбцом. Складываем 4-ый столбец со 2-ым, записываем 2-ым столбцом. Складываем 3-ий столбец с 4-ым, умноженным на ( -1) , записываем 3-им
столбцом. В результате: |
|
|
|
|
|
|
|
|||||||
|
|
-20 |
-14 |
4 |
-11 |
|
-20 |
-14 |
4 |
|
-10 |
-7 |
2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
||||||||||
|
|
0 |
0 |
0 |
-1 |
|
|
|
||||||
|
|
= - |
10 10 |
0 |
= -2 ×10 |
1 |
1 0 |
|
||||||
|
|
10 |
10 |
0 |
5 |
|
22 |
18 |
-3 |
|
22 |
18 |
-3 |
|
|
|
22 |
18 |
-3 |
13 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Складываем 1-ый столбец со 2-ым, умноженным на ( -1) , записываем 1-ым
столбцом. В итоге: |
|
|
|
|
||||||
-20 |
|
-3 |
-7 |
2 |
|
= -20 |
|
-3 2 |
|
= -20 ×( 9 - 8) = -20 . |
|
|
|
|
|||||||
|
|
|
|
|||||||
|
0 |
1 |
0 |
|
|
|
||||
|
|
4 |
18 |
-3 |
|
|
|
4 -3 |
|
|
|
|
|
|
|
|
|
|
|||
Ответ: = −20 .
ПРИМЕР 5. Доказать совместность системы
8

ì 2х1 + 7х2 +13х3 = 0 ïí3х1 +14х2 +12х3 =18 и решить:
ïî5х1 + 25х2 +16х3 = 39 а) методом Гаусса, б) методом Крамера,
в) методом обратной матрицы.
РЕШЕНИЕ: По теореме Кронекера – Капелли система совместна тогда и
только тогда, когда r ( A) = r ( A) .
А) Выпишем расширенную матрицу и преобразуем ее по методу Гаусса:
æ 2 |
7 |
13 |
|
0 |
ö |
||
|
|||||||
|
ç |
3 |
14 |
12 |
|
18 |
÷ |
|
|
||||||
А = ç |
|
÷ . |
|||||
ç |
5 |
25 |
16 |
|
39 |
÷ |
|
è |
|
ø |
|||||
Произведем преобразования:
Умножим 1-ую строку на 3, а 2-ую строку на ( -2) сложим их и запишем 2-ой строкой.
Умножим 1-ую и 2-ую строки на ( -1) и сложим все три строки вместе, запишем 3-ей строкой.
После преобразований получается:
|
|
|
æ 2 |
7 |
13 |
|
0 |
ö |
|
|
|
|
|
||||||
|
|
|
ç |
0 |
-7 |
15 |
|
-36 |
÷ |
A : |
|
||||||||
ç |
|
÷ |
|||||||
|
|
|
ç |
0 |
4 |
-9 |
|
21 |
÷ |
|
|
|
è |
|
|
|
|
|
ø |
Умножим 2-ую строку на 4, а 3-ю на 7, сложим и запишем 3-ей строкой. В итоге получаем cледующую матрицу:
|
|
|
æ 2 |
7 |
13 |
|
0 |
ö |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
ç |
|
|
|
|
|
÷ |
|
|
|
A : |
0 |
-7 15 |
|
-36 |
r(A) = r ( A) = 3 = n . |
|||||||
ç |
|
÷ |
||||||||||
|
|
|
ç |
0 |
0 |
-3 |
|
3 |
÷ |
|
|
|
|
|
|
è |
|
|
|
|
|
ø |
|
|
|
9

Итак, система совместна, так как r(A) = r ( A) и имеет единственное
решение, так как r = n = 3 (n − число неизвестных). Найдем решение:
Из последнего уравнения: −3х3 = 3 Þ х3 = −1.
Из второго уравнения: −7х2 +15х3 = −36 Þ 7х2 = −15 + 36 = −21, х2 = 3 . Из первого уравнения: 2х1 + 7х2 +13х3 = 0 2х1 + 21−13 = 0 , 2х1 = −8 ,
х1 = −4 .
Ответ: х1 = −4 , х2 = 3 , х3 = −1.
Б) Метод Крамера:
|
|
2 |
7 |
13 |
|
||||
|
|
||||||||
D = |
|
А |
|
= |
|
3 |
14 |
12 |
= 2(14 ×16 - 25×12) - 7(3×16 - 5×12) +13(3× 25 - 5×14) = |
|
|
||||||||
|
|
5 |
25 |
16 |
|
||||
= -3 ¹ 0. Раскрыли определитель по 1 строке. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Dх1 = |
|
0 |
|
|
7 |
|
13 |
|
= |
|
0 |
7 |
13 |
|
= 2 |
|
0 |
7 |
13 |
|
= 2 |
|
0 |
7 |
13 |
|
= |
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
18 |
14 |
|
12 |
|
|
18 |
14 |
12 |
|
|
9 |
7 |
6 |
|
|
0 |
16 |
30 |
|
||||||||||||||||||
|
|
|
|
|
39 25 16 |
|
|
|
3 -3 -8 |
|
|
|
3 -3 -8 |
|
|
|
3 -3 -8 |
|
|
|||||||||||||||||||
= 6(210 -16 ×13) =12 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
х = |
|
|
|
|
|
х1 |
|
|
= 12 = −4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
−3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Dх2 = |
|
|
2 |
|
|
0 |
|
13 |
|
= 2(18×16 - 39 ×12) +13(3×39 - 5×18) = -9 . |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
3 |
|
|
18 |
|
12 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
5 |
|
|
39 |
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
х = |
|
|
|
|
|
|
х2 |
= −9 = 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
|
|
|
D |
-3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Dх3 = |
|
2 |
|
|
7 |
|
0 |
|
|
= 2(14 ×39 - 25×18) - 7(3×39 - 5×18) = -9 . |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
3 |
|
|
14 |
|
18 |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
5 |
|
|
25 |
|
39 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
х = |
|
|
|
|
|
|
х3 |
|
= |
3 |
= −1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
−3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
10
