
-
Работа 4. Изучение спектра поглощения молекулы йода.
Цель работы. Изучение строения двухатомных молекул и связи внутримолекулярных движений с оптическими спектрами. Экспериментальное определение границ полосатого спектра поглощения молекулы йода; расчет ее энергии диссоциации, частоты колебаний и постоянной ангармоничности.
Образование молекул. Молекула - наименьшая часть данного вещества, являющаяся носителем его основных химических и физических свойств и способная самостоятельно существовать. Она состоит из различных или одинаковых атомов, соединенных в единое целое химическими связями. Число атомов, входящих в молекулу, колеблется от двух (например, H2, N2, CO и др.) до сотен тысяч (молекулы белков). При образовании химической связи важное значение имеют электростатические силы взаимодействия электронов и ядер атомов. Однако природа химической связи, а также основные физические и химические свойства молекулы могут быть поняты только на основе квантовомеханических представлений.
Очевидно,
что равновесная конфигурация молекулы
характеризуется минимумом потенциальной
энергии (рис. 3.16). Сближение ядер на
расстояние
![]() <
<![]() может совершаться лишь
может совершаться лишь
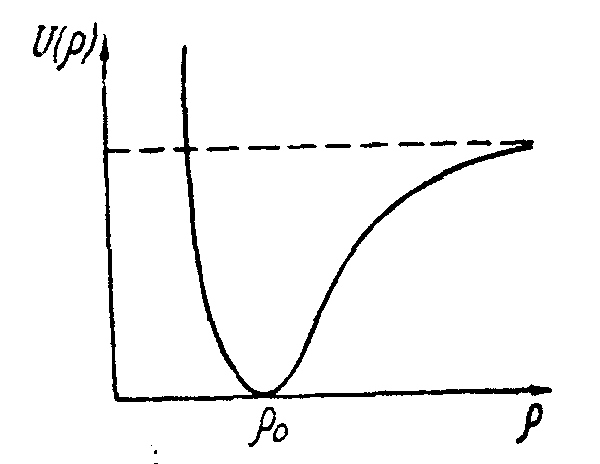
Рис. 3.16.
против
сил отталкивания между ядрами и поэтому
сопровождается резким увеличением
потенциальной энергии. Увеличение
расстояния между ядрами (![]() >
>![]() )
также должно привести к возрастанию
потенциальной энергии, поскольку и для
такого процесса необходимо затратить
работу. При достаточном удалении ядер
друг от друга их взаимодействие
ослабевает, а потенциальная энергия
)
также должно привести к возрастанию
потенциальной энергии, поскольку и для
такого процесса необходимо затратить
работу. При достаточном удалении ядер
друг от друга их взаимодействие
ослабевает, а потенциальная энергия![]() асимптотически
приближается к некоторому пределу,
которому обычно приписывается численное
значение, равное нулю (
асимптотически
приближается к некоторому пределу,
которому обычно приписывается численное
значение, равное нулю (![]() ).
В предельном состоянии молекула
распадается на составные части, т.е.
происходит процесс диссоциации молекулы.
).
В предельном состоянии молекула
распадается на составные части, т.е.
происходит процесс диссоциации молекулы.
Внутримолекулярные виды движения и полная энергия двухатомной молекулы. В отличие от атома в молекуле кроме движения электронов существуют движения, в которых участвуют ядра: колебательное движение ядер относительно положения равновесия и вращение молекулы как целого относительно центра масс. Энергии всех этих движений квантуются, что приводит к новой структуре в схеме энергетических уровней по сравнению с атомом.
Совокупность
значений полной энергии молекулы может
быть определена при решении волнового
уравнения Шредингера, описывающего все
виды движений в молекуле. Однако точное
решение такого уравнения даже в простейшем
случае двухатомной молекулы невозможно.
Тем не менее исследования показали, что
с хорошей степенью приближения полное
уравнение Шредингера может быть разделено
на три решаемых уравнения, соответствующие
электронному, колебательному и
вращательному движениям. Волновая
функция молекулы может быть представлена
в виде произведения
![]() эл
эл![]() кол
кол![]() вр,
а полная энергия молекулы как сумма
энергий, соответствующих трем видам
движения:
вр,
а полная энергия молекулы как сумма
энергий, соответствующих трем видам
движения:
![]() эл
эл![]() кол
кол![]() вр.
Такое разделение является физически
обоснованным. Вследствие огромной
разницы между массами электронов и ядер
электроны движутся намного быстрее и
ядра при рассмотрении движения
электронов можно считать покоящимися.
Однако при исследовании движения
ядер получается хорошее приближение,
вр.
Такое разделение является физически
обоснованным. Вследствие огромной
разницы между массами электронов и ядер
электроны движутся намного быстрее и
ядра при рассмотрении движения
электронов можно считать покоящимися.
Однако при исследовании движения
ядер получается хорошее приближение,

Рис. 3.17.
если пользоваться средними значениями физических величин, относящихся к движению электронов, ибо за время, необходимое для заметного перемещения ядер, электроны совершают огромное количество обращений вокруг них.
Электронная
энергия молекулы. Для
определения электронной части полной
энергии рассматривается молекула с
закрепленными в пространстве ядрами.
Валентные электроны движутся в
электростатическом поле ядер, причем
потенциальная энергия поля должна быть
задана в уравнении Шредингера, описывающем
движение электронов. Поскольку
потенциальная энергия взаимодействия
электронов с ядрами зависит от расстояния
между ядрами, то межъядерное расстояние
![]() войдет в уравнение Шредингера в виде
параметра, а полученные при решении
квантованные значения электронной
энергии будут являться функцией
расстояния
войдет в уравнение Шредингера в виде
параметра, а полученные при решении
квантованные значения электронной
энергии будут являться функцией
расстояния![]() эл,n
эл,n![]() ,
где
,
где![]() -
квантовое число, определяющее электронную
энергию. Таким образом, в отличие от
атомов, разным электронным состояниям
которых соответствуют уровни энергии,
возможным электронным состояниям
двухатомной молекулы может быть
поставлена в соответствие система
кривых
-
квантовое число, определяющее электронную
энергию. Таким образом, в отличие от
атомов, разным электронным состояниям
которых соответствуют уровни энергии,
возможным электронным состояниям
двухатомной молекулы может быть
поставлена в соответствие система
кривых![]() эл,n
эл,n![]() (рис. 3.17), называемых конфигурационными.
Для относительного движения ядер
(рис. 3.17), называемых конфигурационными.
Для относительного движения ядер![]() эл,n
эл,n![]() играет роль потенциальной энергии, и
потому конфигурационные кривые
совпадают с кривыми потенциальной
энергии
играет роль потенциальной энергии, и
потому конфигурационные кривые
совпадают с кривыми потенциальной
энергии![]() .
.
С
увеличением квантового числа
![]() изменяется вид конфигурационной кривой:
уменьшается глубина кривой в минимуме
и положение минимума смещается в сторону
бóльших
изменяется вид конфигурационной кривой:
уменьшается глубина кривой в минимуме
и положение минимума смещается в сторону
бóльших
![]() ,
т. е. равновесное межъядерное расстояние
в возбужденном состоянии увеличивается.
В связи с этим часто уже второе
возбужденное состояние (
,
т. е. равновесное межъядерное расстояние
в возбужденном состоянии увеличивается.
В связи с этим часто уже второе
возбужденное состояние (![]() =3)
в молекуле не реализуется, так как она
становится неустойчивой. Различные
электронные состояния обычно
характеризуют значениями электронной
энергии
=3)
в молекуле не реализуется, так как она
становится неустойчивой. Различные
электронные состояния обычно
характеризуют значениями электронной
энергии![]() эл,n
эл,n![]() в равновесном состоянии (в точке минимума
конфигурационной кривой). Энергетическое
расстояние между последовательными
электронными состояниями составляет,
как и для всех атомов, 1-10 эВ и уменьшается
с увеличением
в равновесном состоянии (в точке минимума
конфигурационной кривой). Энергетическое
расстояние между последовательными
электронными состояниями составляет,
как и для всех атомов, 1-10 эВ и уменьшается
с увеличением![]() .
.
Прочность
химической связи тем больше, чем глубже
минимум на конфигурационной кривой.
Разность энергий
![]() эл,n
эл,n![]()
![]() эл,n
эл,n![]() представляет собой (с точностью до
небольшой поправки) энергию диссоциации
молекулы
представляет собой (с точностью до
небольшой поправки) энергию диссоциации
молекулы![]() .
Наибольшее значение энергия диссоциации
имеет для основного электронного
состояния молекулы (
.
Наибольшее значение энергия диссоциации
имеет для основного электронного
состояния молекулы (![]() =1).
=1).
Колебательная
энергия молекулы. При
постановке задачи о колебании ядер
необходимо в уравнение Шредингера,
описывающее движение ядер, подставить
значение потенциальной энергии,
характеризующей это движение. В качестве
потенциальной энергии следует
использовать
![]() эл,n
эл,n![]() .
Так как различным электронным
состояниям молекулы соответствуют
различные конфигурационные кривые, то
решение задачи о колебании ядер следует
проводить для каждого электронного
состояния молекулы отдельно. Обычно
точный вид зависимости
.
Так как различным электронным
состояниям молекулы соответствуют
различные конфигурационные кривые, то
решение задачи о колебании ядер следует
проводить для каждого электронного
состояния молекулы отдельно. Обычно
точный вид зависимости![]() эл,n
от
эл,n
от
![]() неизвестен. Поэтому при решении
колебательной задачи приходится
использовать не точное значение
неизвестен. Поэтому при решении
колебательной задачи приходится
использовать не точное значение![]()
![]() эл,n
эл,n![]() ,
а подбирать функцию потенциальной
энергии, удовлетворяющую опыту.
,
а подбирать функцию потенциальной
энергии, удовлетворяющую опыту.
М
о д е л ь г а р м о н и ч е с к о г о о с ц
и л л я т о р а.
Вблизи положения равновесия
![]() форма кривой потенциала может быть
получена из разложения
форма кривой потенциала может быть
получена из разложения![]() в ряд Тейлора:
в ряд Тейлора:
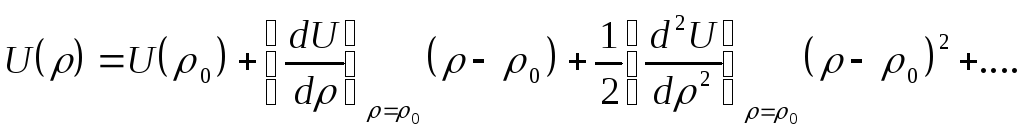
учитывая,
что кривая
![]() имеет минимум
при
имеет минимум
при
![]() (т.е.
(т.е.![]() ),
и принимая за начало отсчета энергии
),
и принимая за начало отсчета энергии![]() ,
получаем
,
получаем
 (3.33)
(3.33)
где
![]() - коэффициент жесткости связи.
Потенциальной функции (3.33) соответствуют
колебания гармонического осциллятора
с частотой
- коэффициент жесткости связи.
Потенциальной функции (3.33) соответствуют
колебания гармонического осциллятора
с частотой![]() кол
кол![]() ,
где
,
где![]() - приведенная
масса осциллятора. Задача о гармоническом
осцилляторе в квантовой механике
решается точно. Возможные значения
его энергии определяются выражением
- приведенная
масса осциллятора. Задача о гармоническом
осцилляторе в квантовой механике
решается точно. Возможные значения
его энергии определяются выражением
![]() кол
кол![]() ,
где
,
где![]() -
постоянная Планка;
-
постоянная Планка;![]() =0,1,2,
...- колебательное квантовое число.(В
этой работе следует различать
=0,1,2,
...- колебательное квантовое число.(В
этой работе следует различать
![]() -
колебательное квантовое число и
-
колебательное квантовое число и![]() -
частоту.)
Нижнему колебательному состоянию
соответствует энергия
-
частоту.)
Нижнему колебательному состоянию
соответствует энергия
![]() кол,
т. е. колебания в молекуле никогда не
могут прекратиться (нулевые колебания).
Потенциальная кривая и уровни энергии
гармонического осциллятора представлены
на рис. 3.18.
кол,
т. е. колебания в молекуле никогда не
могут прекратиться (нулевые колебания).
Потенциальная кривая и уровни энергии
гармонического осциллятора представлены
на рис. 3.18.
