Значения оценок

	В1	В2	В3	В4	В5
A1	6				11
A2			7	5	8
A3	10	5	4

Так как все условия оптимальности выполнены, то полученный план является оптимальным. Транспортная задача решена.

Оптимальный план грузоперевозок

Поставщик	Потребитель												Запасы
	В1			В2		В3			В4		В5
A1		22			14		16			28		0	350	0
				110		200			40
A2		19			17		26			36		0	200	3
	170			30
A3		37			30		31			39		0	300	11
									155		145
Потребность	170			140		200			195		145
	16		14			16		28			-11

Стоимость перевозок при этом = 15645.

145 единиц груза из хранилища A₃ осталось нераспределенным.

Графически оптимальный план грузоперевозок можно представить в виде графа со значения перевозок на дугах (Рис. 1).

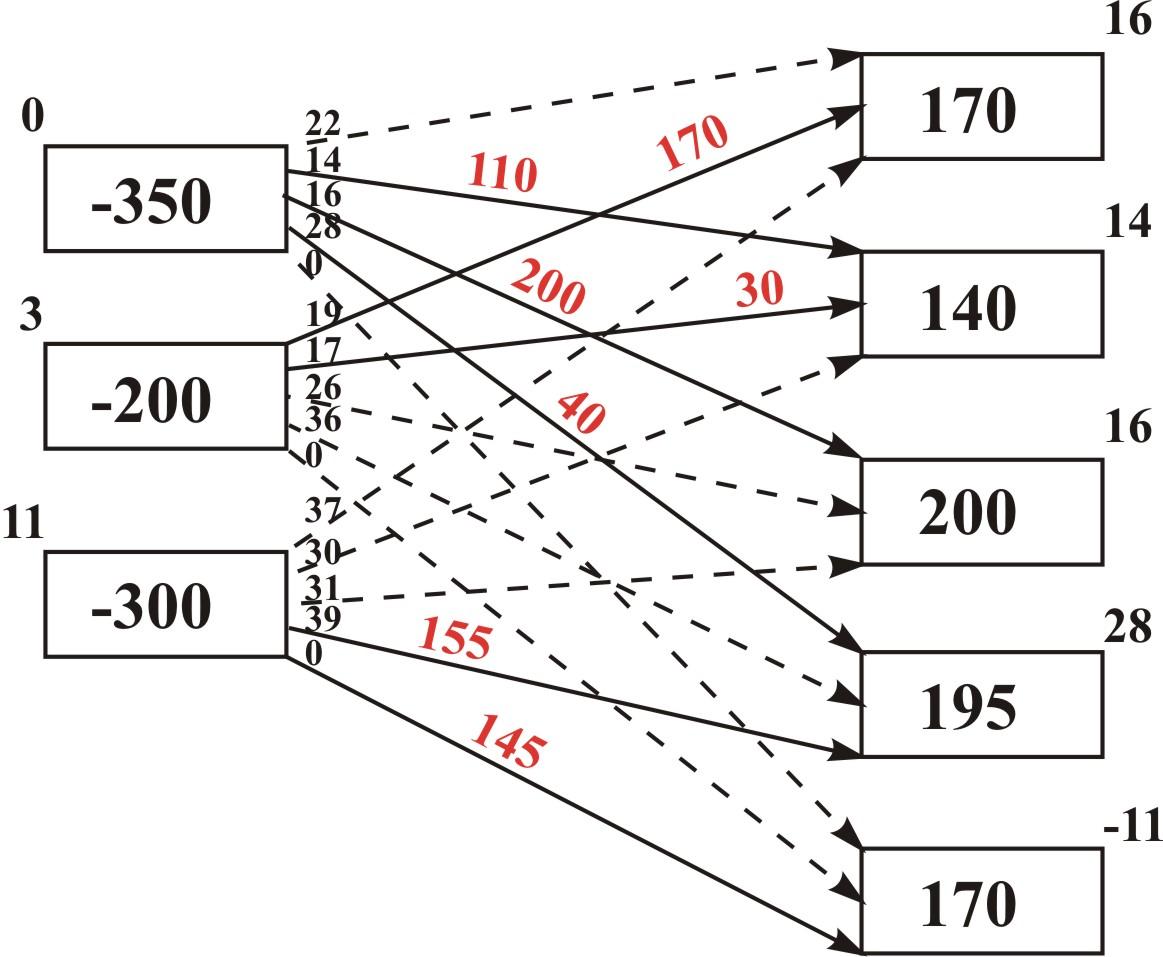
Рис. 1. Граф оптимального плана грузоперевозок.

4. Задача об аренде оборудования Планы аренды. Постановка задачи.

Некоторая фирма (пункт проката) предоставляет в аренду ценное оборудование. Предположим, что другая фирма планирует иметь это оборудование в течение времени и может брать в аренду (оформлять аренду) в определенные моментыгдеТаким образом, имеютсяN отрезков времени , вначале которых можно брать оборудование в аренду (в другой трактовке – покупать новое оборудование), пользоваться им в течение некоторого целого числа отрезков, а в конце какого-либо отрезка возвращать (в другой трактовке – списывать). Отрезками времени могут быть месяцы, дни, недели, часы и т.п., причем один отрезок может состоять, например, из двух недель, другой – из целого квартала, третий – из четырех дней и так далее. В дальнейшем отрезки для определенности будем называтьмесяцами , а момент начала отрезка (началаi-го месяца) будем обозначать просто через i . Таким образом, в аренду оборудование можно брать в моменты i=1,2,…,N и возвращать в моменты j=2,3,…,N+1.

Планом аренды называется последовательность очередных моментов оформления аренды (и возврата оборудования). В наших обозначениях – это возрастающая последовательность натуральных чисел . Общее количество планов аренды наN месяцев совпадает с числом всех подмножеств {2, 3, ,N} и равно 2^{N - 1} .

Примеры планов аренды:

1. (1,2,3,…,7) - план аренды на 6 месяцев, состоящий в том, аренда оформляется 6 раз – каждый раз на 1 месяц;

2. (1, 3, 5, 7) - план аренды на 6 месяцев, состоящий в том, аренда оформляется 3 раза – каждый раз на 2 месяца;

3. (1, 3, 7) - план аренды на 6 месяцев, состоящий в том, аренда оформляется 2 раза – первый раз на 2=3-1 месяца (первый и второй), второй раз на 4 месяца (третий, четвертый, пятый и шестой);

4. (1, 15) план аренды на 14 месяцев, состоящий в том, аренда оформляется 1 раз – с начала 1-го месяца на весь срок – до конца 14 -го месяца.

Предположим теперь , что фирма, предлагающая оборудование в аренду, установила заранее значения арендной платы (стоимости аренды) на все возможные отрезки времени. Пусть C_ij – стоимости аренды от начала i-го месяца до начала j-го месяца в некоторых единицах (у.е.), где 1 ≤ i < j ≤ N+1. Тогда несложно видеть, что число является суммарной арендной платой за весь период, то естьстоимостью плана аренды.

Простейшая задача об аренде (замене) оборудования состоит в нахождении при заданной таблице стоимостей аренды самого дешевого (самых дешевых, если их несколько) плана аренды, то есть оптимального плана аренды.

Пример. Пусть при N=3 cтоимости аренды C_ij заданы в таблице

j i	2	3	4
1	4	9	15
2	–	6	10
3	–	–	6

Из 4 планов аренды

1) (1,2,3,4), С=4+6+6=16;

2) (1,2,4), С=4+10=14;

3) (1,3,4), С=9+6=15;

4) (1,4), С=15

план (1,2,4), то есть план "взять в аренду на 1мес. + 2 мес." является оптимальным планом со стоимостью С^min =14 у.е.