
- •1. Физический смысл первой производной
- •2. Производная второго порядка. Производная n-го порядка.
- •Механический смысл второй производной.
- •Вопросы для самопроверки
- •Геометрический смысл производной
- •1. Понятие касательной и нормали к кривой
- •Геометрический смысл производной
- •Решение задач
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •Упражнения
- •4. Вычислить значения функции в точках экстремума и.
- •5. При необходимости построить схематически график.
- •Вопросы для самопроверки
- •Упражнения
- •Задания для самостоятельного решения
- •На монотонность и экстремумы
Вопросы для самопроверки
Дайте определение касательной к кривой.
Что называется нормалью к кривой?
В чём заключается геометрический смысл производной? Запишите формулу.
Запишите уравнение касательной к кривой в данной точке.
Запишите уравнение нормали к кривой в данной точке.
Задачи для самостоятельного решения
Найти угловой коэффициент касательной, проведённой к кривой

в
точке
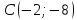 .
.
Кривая задана уравнением
 Определить углы наклона касательных
к положительному направлению оси
Определить углы наклона касательных
к положительному направлению оси ,
проведённых к кривой в точках в точках
с абсциссами
,
проведённых к кривой в точках в точках
с абсциссами .
.На кривой
 найти точку, в которой касательная
параллельна прямой
найти точку, в которой касательная
параллельна прямой .
.В какой точке касательная к кривой
 :
а) параллельна оси
:
а) параллельна оси ;
б) образует с осью
;
б) образует с осью угол 45
угол 45 ?
?Найти абсциссу точки параболы
 , в которой касательная параллельна
оси абсцисс.
, в которой касательная параллельна
оси абсцисс.Найти угловой коэффициент касательной, проведённой к кривой
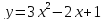
в
точке
 .
.
В какой точке касательная к кривой
 образует с осью
образует с осью угол 30
угол 30 ?
?В какой точке касательная к графику функции
 образует угол 135
образует угол 135
с
осью
 ?
?
В какой точке касательная к графику функции
 параллельна оси абсцисс?
параллельна оси абсцисс?В каких точках угловой коэффициент касательной к кубической параболе
 равен 3?
равен 3?Найти угол наклона касательной к кривой
 в точке, абсцисса которой равна 2.
в точке, абсцисса которой равна 2.Составить уравнение касательной к параболе
 в точке с абсциссой
в точке с абсциссой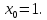
Составить уравнение касательной к гиперболе
 в точке
в точке
Составить уравнение касательной к кривой
 в точке
в точке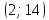 .
.Найти касательную к кривой
 в точке с абсциссой
в точке с абсциссой .
.
Урок № 12
Т е м а. ИССЛЕДОВАНИЕ ФУНКЦИИ НА МОНОТОННОСТЬ С ПОМОЩЬЮ ПРОИЗВОДНОЙ
Рассмотрим приложение производной к исследованию функции на возрастание и убывание.
Признаки возрастания и убывания функции.
Теорема 1 (признак возрастания функции). Если дифференцируемая функция
 возрастает
на данном интервале, то производная
этой функции не отрицательна
на этом интервале.
возрастает
на данном интервале, то производная
этой функции не отрицательна
на этом интервале.
Теорема 2 (признак убывания функции). Если дифференцируемая функция
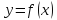 убывает
на данном интервале, то производная
этой функции не положительна
на этом интервале.
убывает
на данном интервале, то производная
этой функции не положительна
на этом интервале.

Обратные теоремы также справедливы.
Теорема
3 (признак возрастания функции).
Если производная функции

положительна
на некотором интервале, то функция на
этом интервале монотонно возрастает.

Теорема
4 (признак убывания функции).
Если производная функции

отрицательна
на некотором интервале, то функция на
этом интервале монотонно убывает.
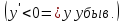
Эти
утверждения можно пояснить геометрически.






















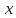
Если
функция возрастает, то и
и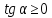 ,
а это возможно только при
,
а это возможно только при
 .
Следовательно, угол наклона касательной
– острый.
.
Следовательно, угол наклона касательной
– острый.
Если
функция убывает, то и
и ,
а это возможно только при
,
а это возможно только при .
Следовательно, угол наклона касательной
– тупой.
.
Следовательно, угол наклона касательной
– тупой.
Такие рассуждения приводят к выводу: на промежутке монотонности (возрастания или убывания) производная свой знак не меняет.
Изменение
характера монотонности происходит при
изменении знака производной
 .
А это возможно лишь при переходе
производной через ноль
.
А это возможно лишь при переходе
производной через ноль или
через точку, в которой производная не
существует (точка
или
через точку, в которой производная не
существует (точка .
.








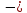

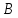




Из этих рассуждений следует правило нахождения промежутков монотонности.
Правило исследования функции на монотонность
Найти производную функции
 .
.Найти точки, в которых производная
 или
или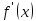 не существует.
не существует.
Эти
точки называются критическими точками
для функции
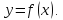
Отметить критические точки на числовой прямой и определить знак производной
 в каждом из полученных интервалов,
входящих в область определения функции.
в каждом из полученных интервалов,
входящих в область определения функции.По полученным знакам производной сделать вывод о характере монотонности: если
 ,
то функция возрастает;
,
то функция возрастает;
если
 ,
то функция убывает.
,
то функция убывает.
П
р и м е р. Найти
промежутки монотонности функции
 .
.
Решение. 1) Найдём производную функции

2)Найдём критические точки
 ,
если 3
,
если 3 или
или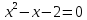 (разделили на 3).
(разделили на 3).
Решив
уравнение, получим
 и
и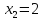 .
.
Отметим критические точки на числовой прямой и определим знак производной












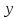
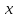



-1 2
Вывод: функция возрастает при

функция
убывает при

