
- •1. Физический смысл первой производной
- •2. Производная второго порядка. Производная n-го порядка.
- •Механический смысл второй производной.
- •Вопросы для самопроверки
- •Геометрический смысл производной
- •1. Понятие касательной и нормали к кривой
- •Геометрический смысл производной
- •Решение задач
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Вопросы для самопроверки
- •Упражнения
- •4. Вычислить значения функции в точках экстремума и.
- •5. При необходимости построить схематически график.
- •Вопросы для самопроверки
- •Упражнения
- •Задания для самостоятельного решения
- •На монотонность и экстремумы
Геометрический смысл производной
1. Понятие касательной и нормали к кривой
Мы знаем аналитический и физический смысл производной:
аналитический
смысл – это
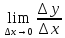 , физический – это скорость процесса,
заданного функцией. Выясним геометрический
смысл производной.
, физический – это скорость процесса,
заданного функцией. Выясним геометрический
смысл производной.
Для этого введём понятие касательной к кривой в данной точке.
Из школьного курса геометрии, вы знаете понятие касательной к окружности. Касательная к окружности определяется как прямая, лежащая в одной плоскости с окружностью и имеющая с ней единственную общую точку.
Но
такое определение касательной неприменимо
для случая произвольной кривой.
Например, для параболы
 оси
оси имеют по одной общей точке с параболой.
Однако ось
имеют по одной общей точке с параболой.
Однако ось является касательной к параболе, а ось
является касательной к параболе, а ось – нет.
– нет.




M1 Дадим общее определение касательной к
M2 кривой в данной точке.
М3
Пусть
 –
некоторые точки произвольной
кривой
–
некоторые точки произвольной
кривой – секущая кривой.
– секущая кривой.
К
При приближении точки
 по кривой секущая
по кривой секущая будет поворачиваться вокруг точки
будет поворачиваться вокруг точки ,
занимая положения
,
занимая положения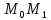 ,
,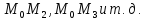

Определение.
Предельное
положение секущей
 при неограниченном приближении точки
при неограниченном приближении точки по кривой называетсякасательной
к
кривой в точке
по кривой называетсякасательной
к
кривой в точке
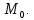
Определение.
Нормалью
к кривой в точке
 называется прямая, проходящая через
точку
называется прямая, проходящая через
точку перпендикулярно касательной к кривой
в этой точке.
перпендикулярно касательной к кривой
в этой точке.


 Если
Если
 – касательная к кривой
– касательная к кривой в точке
в точке ,
,
то
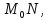 перпендикулярная
перпендикулярная будет нормалью к кривой
будет нормалью к кривой в точке
в точке

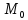
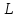

Геометрический смысл производной
Пусть
кривая
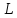 является графиком функции
является графиком функции .
Точки
.
Точки
лежат
на графике функции. Прямая
 - секущая кривой
- секущая кривой .
. – касательная к кривой
– касательная к кривой .
.

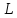




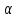 -
угол наклона касательной
-
угол наклона касательной

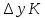




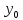



0




Производная
функции
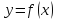 в точке
в точке равна тангенсу угла наклона
касательной, проведённой в точке
равна тангенсу угла наклона
касательной, проведённой в точке или
угловому коэффициенту касательной к
графику функции в этой точке.
или
угловому коэффициенту касательной к
графику функции в этой точке.


Уравнение
касательной
к кривой
 в точке
в точке имеет вид
имеет вид


Уравнение
нормали
к кривой
 в точке
в точке имеет вид
имеет вид


Решение задач
П
р и м е р 1. Вычислите
угловые коэффициенты касательных к
параболе
 в точках
в точках .
.
Решение.
Из геометрического смысла производной
(формула 1) угловой коэффициент касательной
 .
.
Найдём
производную функции:
 .
.
Найдём значение производной в точке

 .
Следовательно,
.
Следовательно,
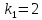 .
.
Найдём значение производной в точке

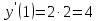 .
Следовательно,
.
Следовательно,
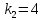 .
.
П
р и м е р 2. У
параболы
 проведены касательные в точках
проведены касательные в точках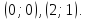 Найдите углы наклона касательных к оси
Ох.
Найдите углы наклона касательных к оси
Ох.
Решение.
По формуле (1)

Найдём
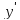 .
. .
.
Вычислим значение производной в точке
 :
: .
.
Следовательно,
 и
и .
.
Аналогично в точке

 .
.
Следовательно,
 и
и
П
р и м е р 3.
В какой точке касательная к кривой
 наклонена к оси Ох
наклонена к оси Ох
под
углом

Решение.
По формуле (1)

 ;
;
 .
Следовательно,
.
Следовательно, и
и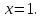
Подставив
 в функцию
в функцию ,
получим
,
получим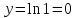 .
Получили точку
.
Получили точку .
.
П
р и м е р 4.
Составить уравнение касательной и
нормали к параболе
 в точке
в точке
Решение.
Уравнение
касательной к кривой имеет вид
 .
.
Из
условия задачи
 .
Найдём производную
.
Найдём производную .
.
 ;
;
 .
.
Подставив
все значения в уравнение
 получим уравнение касательной
получим уравнение касательной
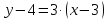 или
или
 .
.
Составим
уравнение нормали, воспользовавшись
формулой
 :
:
 или
или

