
MO_2
.docМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Воронежский государственный архитектурно-строительный университет»
1095
Кафедра высшей математики
Математика
Программа и контрольные задания № 2
ко 2-й части (2 семестр) курса математики для
студентов бакалавриата заочного обучения направления
«Менеджмент организации»
Воронеж 2015
УДК 51:625.08(07)
ББК 22.1:38.6−5я73
Составители
М.Ю. Глазкова, А.И. Барсуков, Л.В. Акчурина
Математика: программа и контрольные задания № 2 ко 2-й части (2 семестр) курса математика для студентов бакалавриата заочного обучения направления «Менеджмент организации» / Воронежский ГАСУ; сост.: М.Ю. Глазкова, А.И. Барсуков, Л.В. Акчурина. – Воронеж, 2015. – 18 с.
Приводятся программа и контрольные задания № 2 ко 2-й части (2 семестр) курса математика. Даны ссылки на литературу, которой можно пользоваться при подготовке к экзамену и выполнении контрольных работ.
Предназначены для студентов бакалавриата 1-го курса заочного обучения направления «Менеджмент организации».
Библиогр.: 6 назв.
УДК 51:625.08(07)
ББК 22.1:38.6−5я73
Печатается по решению учебно-методического совета
Воронежского ГАСУ
Рецензент – Шальнев О.Г. к.э.н., доц. кафедры экономики и основ предпринимательтсва

1. В магазин поступило 30 холодильников, пять из них имеют заводской дефект. Случайным образом выбирается один холодильник. Какова вероятность того, что он будет без дефекта.
2. В коробке находится шесть одинаковых по форме и близких по диаметру сверл. Случайным образом сверла извлекаются из коробки. Какова вероятность того, что сверла извлекаются в порядке возрастания их диаметра?
3. Из 100 изготовленных деталей 10 имеют дефект. Для проверки были отобраны пять деталей. Какова вероятность того, что среди отобранных деталей две окажутся бракованными?
4. В партии из 15 однотипных стиральных машин пять машин изготовлены на заводе А, а 10 – на заводе В. Случайным образом отобрано 5 машин. Найти вероятность того, что две из низ изготовлены на заводе А.
5. Комиссия по качеству раз в месяц проверяет качество продуктов в двух из 30 магазинов, среди которых находятся и два известных вам магазина. Какова вероятность того, что в течение месяца они оба будут проверены?
6. Найти вероятность того, что наудачу взятое двузначное число окажется кратным 2, либо 5, либо тому и другому числу одновременно.
7. Производственное собрание из 5 человек садится за круглый стол. Найти вероятность того, что два определенных лица окажутся рядом.
8. Вероятность правильного оформления счета на предприятии составляет 0,95. Во время аудиторской проверки были взяты два счета. Какова вероятность того, что только один из них оформлен правильно?
9. Вероятность правильного оформления накладной при передаче продукции составляет равна 0,8. Найти вероятность того, что из трех накладных только две оформлены правильно?
10. На строительной площадке складированы плиты перекрытий в количестве 80 штук, среди которых есть 5 бракованных (с трещиной). Краном поднимают для погрузки плиту. Найти вероятность того, что эта плита окажется: а) бракованной; б) годной.
11. В группе 17 юношей и 12 девушек. Из них выбрано 7 человек. Какова вероятность, что среди них 3 девушки?
12. Найти вероятность того, что при бросании двух кубиков хотя бы на одном выпадет число 6.
13. В ящике 100 деталей, из них 10 бракованных. Найти вероятность, что:
нет бракованных; все бракованные.
14. В группе 12 студентов, среди которых 8 отличников. По списку выбрали 9
человек. Найти вероятность, что среди них 5 отличников.
15. В урне 10 красных, 15 синих и 5 белых шаров. Из нее вынимают наугад один
шар. Какова вероятность того, что этот шар не белый?
16. Какова вероятность, что наугад взятое двузначное число из одинаковых
цифр; не из одинаковых цифр?
17. Электронный прибор состоит из 2 последовательно включенных блоков.
Вероятность выхода из строя за один месяц работы I блока – 1/3; II – 1/4, а
двух вместе – 1/6. Найдите вероятность безаварийной работы прибора в
течение месяца.
18. Вероятность попадания в мишень одного стрелка 0,65, а второго – 0,6.
Найти вероятность попадания в мишень при одновременном выстреле двоих.
19. Список вопросов к экзамену из трех разделов.
В I – 40 вопросов, из них студент знает 30;
во II – 30 вопросов, из них студент знает 15;
в III - 30 вопросов, из них студент знает 10.
Билет содержит по одному вопросу из каждого раздела. Какова вероятность
Правильного ответа по билету?
20. В ящике пуговицы: 50 белых, 20 красных, 20 зеленых и 10 синих. Какова
Вероятность, что взятая пуговица синего или зеленого цвета?
21-40.
На сборочное
предприятие поступили однотипные
комплектующие с трех заводов в количестве:
![]() ,
,
![]() ,
,![]() соответственно. Вероятность качественного
изготовления изделий на первом заводе
соответственно. Вероятность качественного
изготовления изделий на первом заводе
![]() ,
на втором
,
на втором
![]() ,
на третьем
,
на третьем
![]() .
Какова вероятность того, что взятое
случайным образом изделие будет
качественным?
.
Какова вероятность того, что взятое
случайным образом изделие будет
качественным?
|
№ |
|
|
|
|
|
|
|
21 |
25 |
35 |
40 |
0,9 |
0,8 |
0,7 |
|
22 |
15 |
25 |
10 |
0,8 |
0,7 |
0,7 |
|
3 |
40 |
35 |
25 |
0,9 |
0,7 |
0,9 |
|
24 |
25 |
10 |
15 |
0,7 |
0,9 |
0,8 |
|
25 |
10 |
20 |
20 |
0,9 |
0,8 |
0,6 |
|
26 |
40 |
30 |
30 |
0,8 |
0,8 |
0,9 |
|
27 |
20 |
50 |
30 |
0,8 |
0,9 |
0,8 |
|
28 |
35 |
35 |
30 |
0,7 |
0,8 |
0,9 |
|
29 |
15 |
45 |
40 |
0,9 |
0,8 |
0,9 |
|
30 |
40 |
15 |
45 |
0,8 |
0,7 |
0,8
|
|
31 |
20 |
15 |
15 |
0,9 |
0,9 |
0,8 |
|
32 |
14 |
26 |
10 |
0,8 |
0,5 |
0,6 |
|
33 |
15 |
15 |
20 |
0,6 |
0,7 |
0,8 |
|
34 |
30 |
20 |
50 |
0,6 |
0,4 |
0,9 |
|
35 |
10 |
20 |
20 |
0,5 |
0,9 |
0,8 |
|
36 |
24 |
16 |
10 |
0,8 |
0,9 |
0,7 |
|
37 |
23 |
17 |
10 |
0,3 |
0,8 |
0,7 |
|
38 |
15 |
25 |
10 |
0,7 |
0,6 |
0,9 |
|
39 |
22 |
18 |
10 |
0,8 |
0,8 |
0,9 |
|
40 |
11 |
19 |
20 |
0,7 |
0,7 |
0,9 |
41-60.
Три плотника могут изготовить одно и
то же изделие. Вероятность представить
готовое изделие без брака для них,
соответственно, равны
![]() .
Составить закон распределения случайной
величины X
– числа готовых изделий без брака, найти
ее математическое ожидание, дисперсию
и среднее квадратическое отклонение.
.
Составить закон распределения случайной
величины X
– числа готовых изделий без брака, найти
ее математическое ожидание, дисперсию
и среднее квадратическое отклонение.
41.
![]() 42.
42.
![]()
43.
![]() 44.
44.
![]()
45.
![]() 46.
46.
![]()
47.
![]() 48.
48.
![]()
49.
![]() 50.
50.
![]()
51.
![]() ;
;
![]() ;
;
![]() .
52.
.
52.
![]() ;
;
![]() ;
;
![]()
53.
![]() ;
;
![]() ;
;
![]() 54.
54.
![]() ;
;
![]() ;
;
![]()
55.
![]() ;
;
![]() ;
;
![]() 56.
56.
![]() ;
;
![]() ;
;
![]()
57.
![]() ;
;
![]() ;
;
![]() 58.
58.
![]() ;
;
![]() ;
;
![]()
59.
![]() ;
;
![]() ;
;
![]() 60.
60.
![]() ;
;
![]() ;
;
![]()
61-80.
Задана
функция распределения
![]() случайной величины X.
Найти функцию
плотности
случайной величины X.
Найти функцию
плотности
![]() ,
математическое ожидание, дисперсию и
среднее квадратическое отклонение
случайной величины X.
,
математическое ожидание, дисперсию и
среднее квадратическое отклонение
случайной величины X.
61.
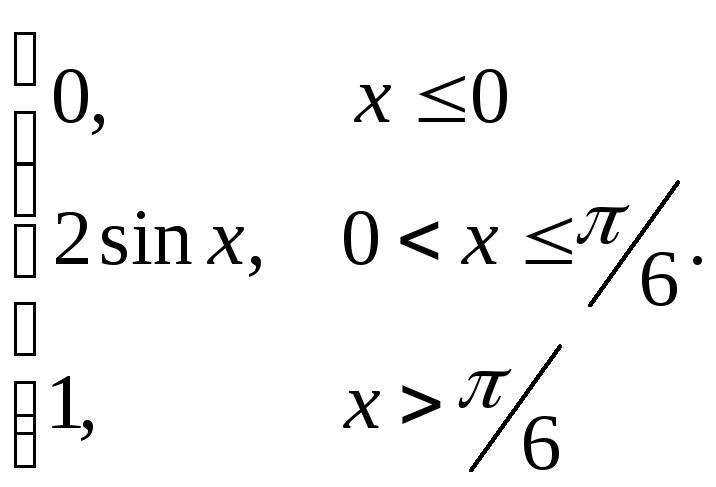 62.
62.

63.
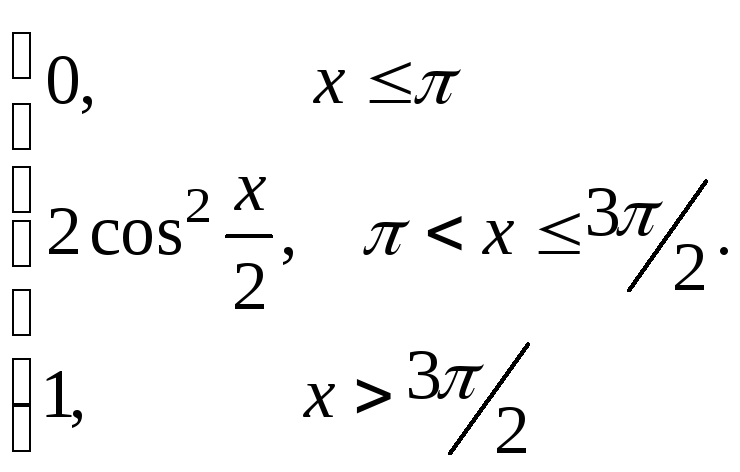 64.
64.
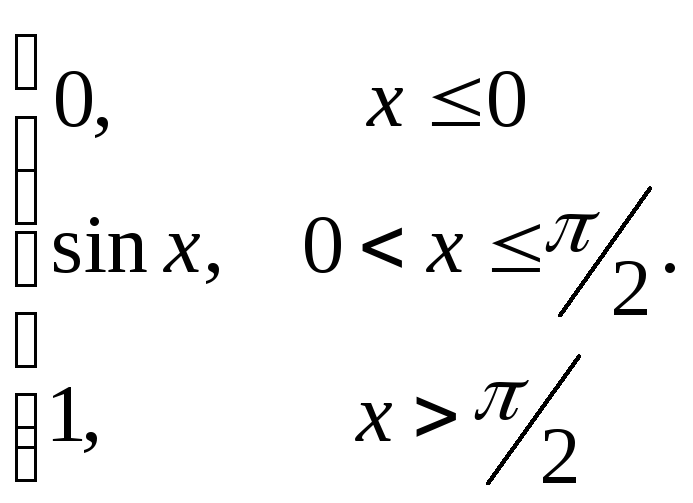
65.
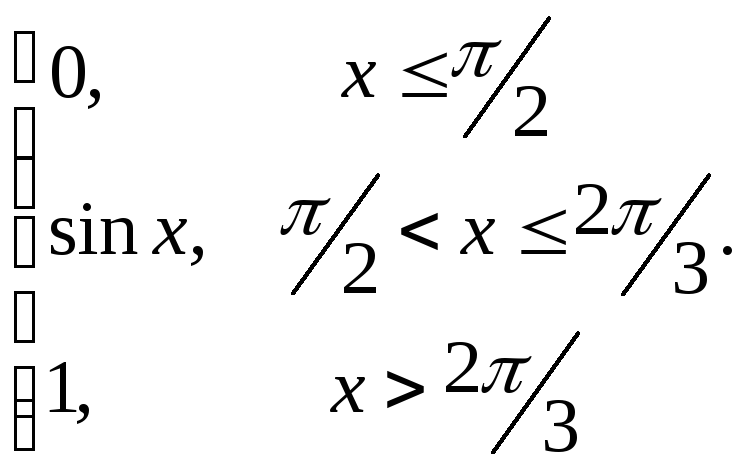 66.
66.

67.
 68.
68.

69.
 70.
70.

71.
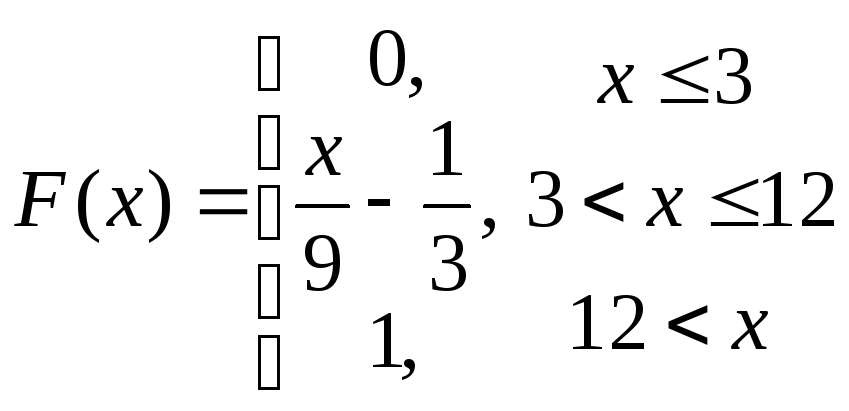 72.
72.
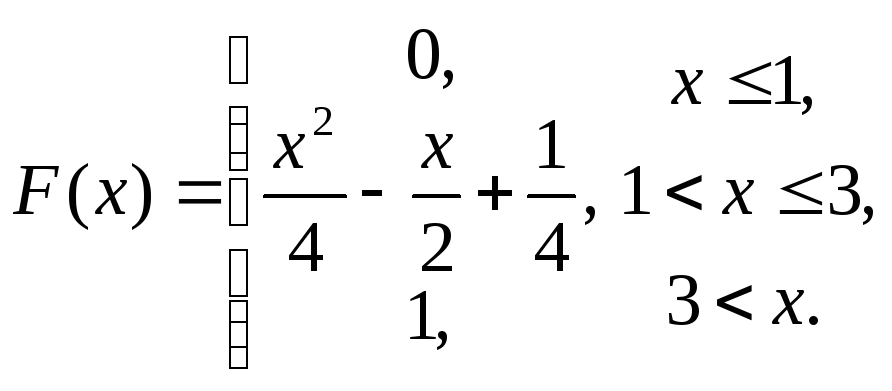
73.
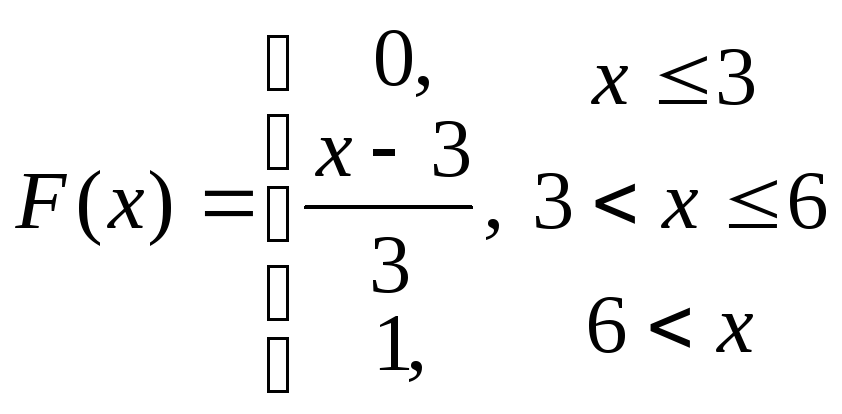 74.
74.
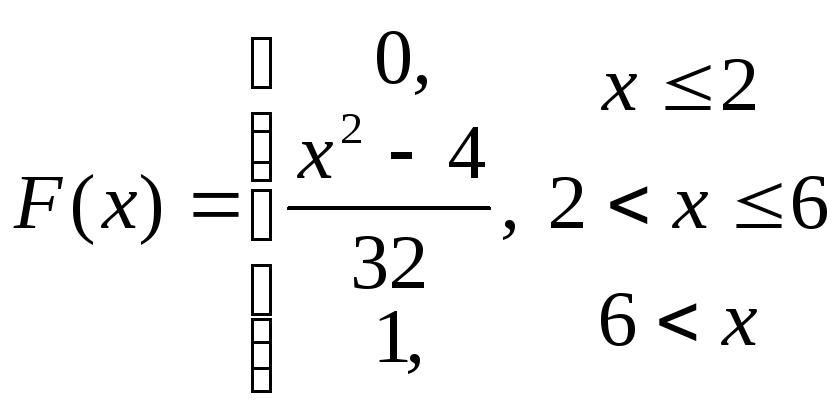
75.
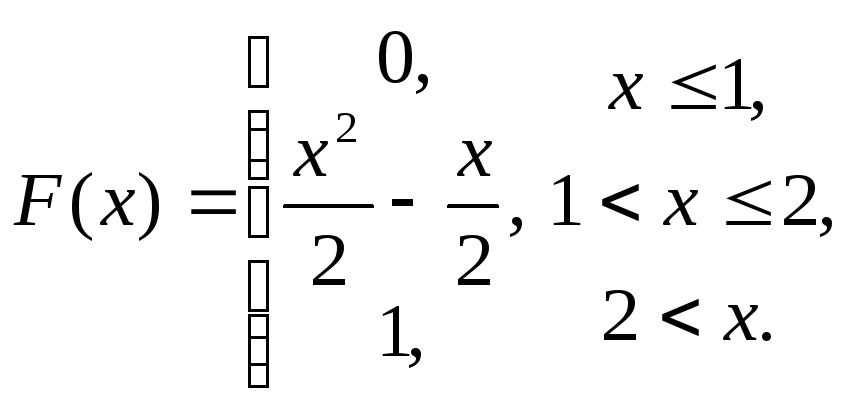 76.
76.

77.
 78.
78.
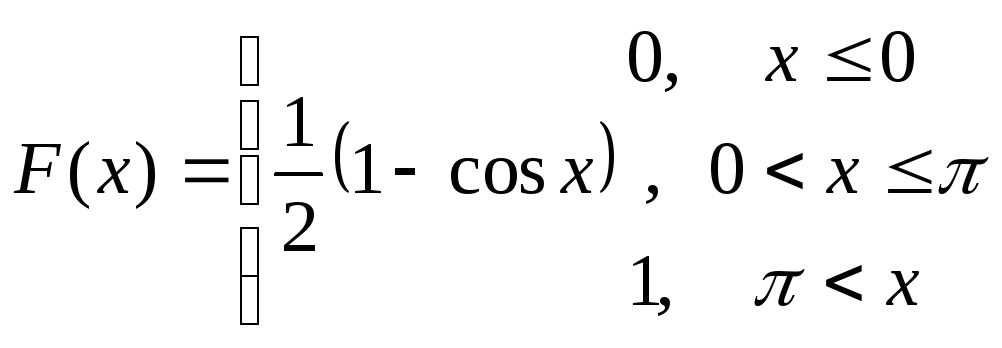
79.
 80.
80.
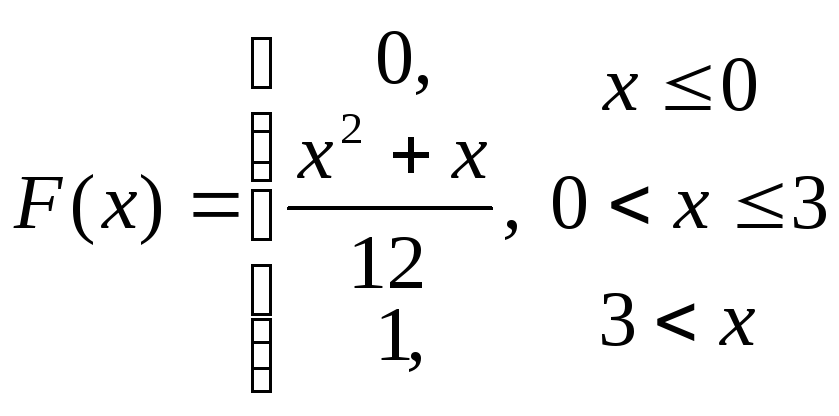
81-100. Найти выборочное уравнение линейной регрессии Y на X на основании корреляционной таблицы.
81.
|
X |
10 15 20 25 30 35 |
|
Y |
6 4 6 8 21 2 5 4 12 6 1 5
|
|
15 25 35 45 55 |
82.
|
X |
20 25 30 35 40 45 |
|
Y |
4 8 4 2 4 2 10 8 4 10 4
|
|
10 20 30 40
|
83.
|
X |
5 10 15 20 25 30 |
|
Y |
4 6 8 4 8 10 6 32 4 12 6 |
|
14 24 34 44
|
84.
|
X |
15 20 25 30 35 40 |
|
Y |
2 1 7 4 2 3 5 10 5 2 3 1 2 3 |
|
100 120 140 160
|
85.
|
X |
20 25 30 35 40 45 |
|
Y |
4 2 1 2 1 3 8 5 4 2 1 3 3 2 10 3 2 1 3 8 2 |
|
105 115 125 135 145
|
86.
|
X |
10 15 20 25 30 35 |
|
Y |
6 4 6 8 20 2 5 5 12 6 1 5
|
|
15 25 35 45 55 |
87.
|
X |
10 15 20 25 30 35 |
|
Y |
4 2 1 2 1 3 8 5 4 2 1 3 3 2 10 3 2 1 3 9 1 |
|
14 24 34 44 54 |
88.
|
X |
10 15 20 25 30 35 |
|
Y |
1 5 7 4 2 4 6 5 3 5 4 6 10 2 3 5 2 4 4 8 10
|
|
20 40 60 80 100 |
89.
|
X |
5 10 15 20 25 30 |
|
Y |
6 4 2 2 4 2 8 1 5 10 7 1 5 3 8 6 7 9 5 4 1 |
|
15 25 35 45 55 |
90.
|
X |
5 10 15 20 25 30 |
|
Y |
5 1 4 7 2 6 5 4 3 4 5 6 10 2 3 5 10 4 8 2 4 |
|
80 100 120 140 160 |
91.
|
X |
12 17 22 27 32 37 |
|
Y |
4 3 2 3 1 10 3 5 1 4 8 2 1 1 2 |
|
105 115 125 135 145 |
93.
|
X |
10 15 20 25 30 35 |
|
Y |
4 2 2 2 5 4 3 4 5 6 10 2 3 5 10 4 8 2 4 |
|
14 24 34 44 54 |
94.
|
X |
10 15 20 25 30 35 |
|
Y |
4 2 2 2 5 4 3 4 5 6 1 2 3 5 1 4 8 2 4 |
|
20 40 60 80 100 |
95.
|
X |
12 17 22 27 32 37 |
|
Y |
4 3 2 3 1 1 3 5 1 4 2 2 1 1 2 |
|
10 15 25 35 45 |
96.
|
X |
2 7 12 17 22 27 |
|
Y |
4 3 2 3 1 1 3 2 1 4 2 2 1 1 2 |
|
10 15 25 35 45 |
97.
|
X |
10 15 20 25 30 35 |
|
Y |
1 5 7 4 2 4 6 5 3 5 4 6 10 2 3 5 2 4 4 8 10
|
|
2 4 6 8 10 |
