
- •5. Линейное пространство. Евклидово и унитарное пространства
- •6. Линейные операторы и их свойства
- •Линейные преобразования евклидова пространства
- •7. Действительные числа. Функция действительной переменной. Предел функции. Непрерывные функции.
- •8. Производная и дифференциал. Производные и дифференциалы высших порядков. Формула Тейлора
- •9. Основные теоремы дифференциального исчисления и их применения
- •10. Первообразная и неопределенный интеграл
- •4. Интегрирование некоторых тригонометрических функций.
- •6. Интеграл вида если функцияR является нечетной относительно cosx.
- •11. Определенный интеграл Римана, его свойства. Применения к вычислению геометрических, физических и механических величин Определенный интеграл
- •12. Функции нескольких действительных переменных.
- •13. Частные производные и дифференцируемость ф-ции в точке. Производные и дифференциалы высших порядков. Равенство смешанных производных
- •14. Неявная и обратная функции. Экстремумы
- •15. Числовые ряды и их сходимость.
- •16. Функциональные последовательности и ряды. Степенные ряды. Ряд Тейлора.
- •2) Дифференцирование степенных рядов.
- •3) Сложение, вычитание, умножение и деление степенных рядов.
- •18. Ряды Фурье. Преобразование Фурье. Интеграл Фурье
- •Разложение в ряд Фурье четных и нечетных функций
- •Разложение в ряд Фурье функций произвольного периода
- •Представление непериодической функции ряда Фурье
- •Тригонометрический ряд Фурье в комплексной области
- •Свойства ряда Фурье
- •- Неравенство Бесселя.
- •- Равенство Парсеваля,
- •Понятие об интеграле Фурье и об преобразовании Фурье
- •19. Мера Лебега, измеримые множества и функции
- •20. Интеграл Лебега и его свойства.
- •21. Ф-ции комплексной переменной. Диф-ние и инт-ние. Теорема Коши.
- •22. Ряды Тейлора и Лорана. Вычеты
- •Аналитические функции и их разложение в степенные ряды.
- •Свойства максимума модуля аналитических и гармонических функций.
- •Ряд Тейлора.
- •Ряд Лорана.
- •Изолированные особые точки аналитических функций и их классификация.
- •Вычеты и основная теорема о вычетах.
- •Применение к вычислению интегралов.
- •23. Математическое моделирование и вычислительный эксперимент
- •24. Численные методы в алгебре
- •Обусловленность систем линейных алгебраических уравнений
- •Вычисление определителей и обращение матриц
- •Итерационные методы
- •Достаточное условие сходимости итерационного процесса
- •25. Решение нелинейных уравнений и систем уравнений
- •26. Приближение функций.
- •27. Численное дифференцирование. Численное интегрирование
- •28. Решение обыкновенного дифференциального уравнения первого порядка методами Эйлера, Эйлера – Коши, Рунге – Кутты. Метод конечных разностей.
- •29. Разностные методы решения задач математической физики.
- •33. Линейные уравнения и системы.
- •34.Линейные уравнения и системы с постоянными коэффициентами
- •35. Устойчивость решений дифференциальных уравнений
- •Простейшие типы точек покоя. Автономные динамические системы двух уравнений первого порядка. Типы особых точек на фазовой плоскости
- •№37 Физические задачи, приводящие к уравнению параболического типа
- •Интеграл Пуассона
- •39. Алгебра логики
- •3. Основные законы логики.
- •4. Логические функции.
- •5. Нормальные формы. Совершенные нормальные формы.
- •Алгоритм построения сднф.
- •6. Арифметические операции в алгебре логики. Полином Жегалкина.
- •7. Полнота и замкнутость (примеры полных систем). Теорема Поста.
- •Свойства отношений.
- •40. Графы и их свойства
- •41. Маршруты в графах и деревья
- •41. Маршруты в графах и деревья
8. Производная и дифференциал. Производные и дифференциалы высших порядков. Формула Тейлора
Производной
ф-й
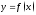 в т.
в т.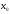 наз. предел отношения приращения ф-и к
приращению аргумента, который стремиться
к 0:
наз. предел отношения приращения ф-и к
приращению аргумента, который стремиться
к 0: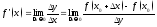 .
.
Если
ф-я
 в т.
в т.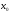 имеет конечную производную, то эта ф-я
наз-ся дифференцируемой в т.
имеет конечную производную, то эта ф-я
наз-ся дифференцируемой в т.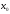 .
Если ф-я
.
Если ф-я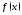 дифференцируема в каждой точке промежутка
дифференцируема в каждой точке промежутка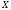 ,
то она наз-ся дифференцируемой на
промежутке
,
то она наз-ся дифференцируемой на
промежутке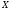 .
Производная ф-и в т. есть двусторонний
предел.
.
Производная ф-и в т. есть двусторонний
предел.
Геометрический смысл производной- тангенс угла наклона касательной к кривой в данной точке.
Используется для построения нормали и касательной к кривой в заданной точке.
Касательной
к кривой в данной т.
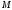 наз-ся предельное положение секущей
наз-ся предельное положение секущей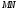 ,
когда т.
,
когда т.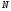 по кривой движется в т.
по кривой движется в т.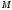 .
.
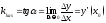
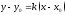 -
прямая с заданным угловым коэффициентом
ч/з т.
-
прямая с заданным угловым коэффициентом
ч/з т.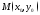 с
с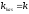 .
.
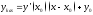 -
Ур-е касательной к зад. кривой в т.
-
Ур-е касательной к зад. кривой в т.
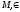 кривой.
кривой.
Нормалью
к кривой в т.
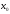 наз-ся прямая,
наз-ся прямая,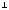 к касательной, проведенной к кривой в
т.
к касательной, проведенной к кривой в
т.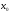 .
.
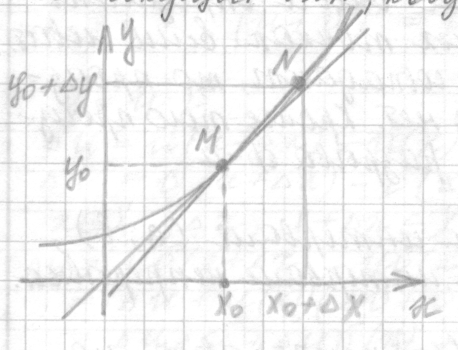
Механический смысл производной:
Это задача о нахождении мгновенной скорости тела.
Теорема.: Если функция дифференцируема, то она непрерывна. Обратное неверно.
Пусть
ф-я
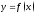 диф-ма в т.
диф-ма в т.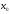 .
Тогда ее приращение м.б. записано в виде
.
Тогда ее приращение м.б. записано в виде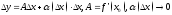 при
при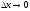 .Дифференциалом
функции наз. главную линейную часть
.Дифференциалом
функции наз. главную линейную часть
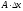 приращения функции и обозначают
приращения функции и обозначают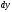 .
.
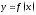 ,
,
 - независимая переменная:
- независимая переменная: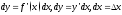 .
.
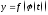 ,
,
 - зависимая переменная:
- зависимая переменная: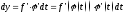 ,
,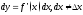 .
.
Формула для записи дифференциала обычной и сложной функции совпадают только по внешнему виду. Это и называют инвариантностью формы первого дифференциала.
Теорема:
пусть
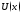 и
и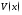 диф-мые в некот. промежутке
диф-мые в некот. промежутке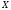 ф-ции. Тогда
ф-ции. Тогда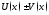 ,
,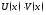 ,
,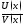 диф-мы в этом промежутке, причем
диф-мы в этом промежутке, причем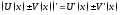 ,
,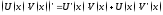 ,
,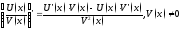 .
.
Док-во:
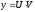 ,
,
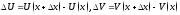 ,
,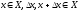 .
.
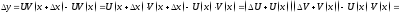
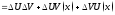
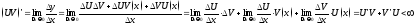
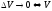 -
диф-ма
-
диф-ма
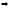 непр.
непр.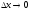 .
.
Производная сложной ф-ции:
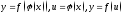 ;
;
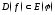 ;
;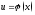 имеет производную, то
имеет производную, то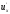 в
в ,
,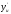 в
в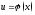 ,
,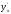 в
в ,
которая вычисляется по формуле
,
которая вычисляется по формуле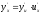 .
.
Производная обратной ф-ции:
Если
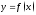 ,
,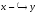 и имеет не = 0 производную
и имеет не = 0 производную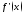 в произвольной точке этого промежутка,
то обратная ей ф-ция
в произвольной точке этого промежутка,
то обратная ей ф-ция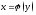 имеет производную в соот-щей точке
имеет производную в соот-щей точке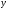 ,
кот вычисляется
,
кот вычисляется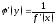 .
.
Док-во:
т.к. ф-я
монотонна и имеет на промежутке
производную, то она на нем непрерывна.
Всякая непрерывная монотонная на
промежутке ф-я имеет обратную, т.е.
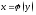 - определена.
- определена.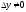 соот-ет
соот-ет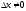 .
Если
.
Если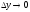 ,
то
,
то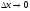 ,
,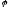 - непрерывна.
- непрерывна.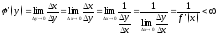 .
.
Производной
 -го
порядка наз.
производная от производной
-го
порядка наз.
производная от производной
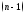 -го
порядка, если эта производная существует.
-го
порядка, если эта производная существует.
Дифференциалом
 -го
порядка наз.
дифференциал от дифференциала
-го
порядка наз.
дифференциал от дифференциала
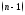 -го
порядка, при условии, что
-го
порядка, при условии, что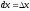 - фиксировано.
- фиксировано.
Если
ф-я
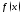 опр. в некот. окрестности т.
опр. в некот. окрестности т.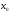 и имеет в этой окрестности производную
до
и имеет в этой окрестности производную
до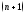 -го
порядка вкл., тогда для
-го
порядка вкл., тогда для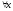 из этой окрестности найдется т.
из этой окрестности найдется т. м/у
м/у и
и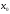 такая, что справедлива формула:
такая, что справедлива формула:
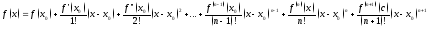 .
Это формула Тейлора.
.
Это формула Тейлора.
Производные основных элементарных функций:

9. Основные теоремы дифференциального исчисления и их применения
Теорема
Ферма:
если-ф-я
опр-на на некот. промежутке
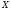 и во внутренней т.
и во внутренней т.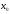 она принимает свое наибольшее или
наименьшее значение, тогда, если в этой
точке сущ. поизводная, то она равна
нулю.
она принимает свое наибольшее или
наименьшее значение, тогда, если в этой
точке сущ. поизводная, то она равна
нулю.
Теорема
Роля.
Пусть ф-я
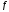 :
1) непрерывна на отрезке
:
1) непрерывна на отрезке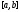 ;
2) дифференцируема в каждой точке
интервала
;
2) дифференцируема в каждой точке
интервала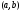 ;
3) принимает равные значения на концах
отрезка, т.е.
;
3) принимает равные значения на концах
отрезка, т.е.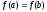 ;
тогда существует хотя бы одна такая
точка
;
тогда существует хотя бы одна такая
точка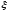 ,
,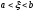 ,
что
,
что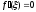 .
.
Доказательство.
Ф-я, непрерывная на отрезке, принимает
наибольшее и наименьшее значение в
некоторых точках этого отрезка. Пусть
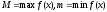 ;
тогда для всех
;
тогда для всех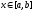 выполняется неравенство
выполняется неравенство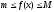 .
Если
.
Если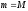 ,
то ф-я
,
то ф-я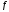 постоянна
и, значит
постоянна
и, значит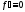 на
на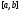 .
В качестве точки
.
В качестве точки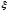 можно взять любую точку интервала
можно взять любую точку интервала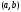 .
Если же
.
Если же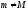 ,
то из условия
,
то из условия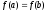 следует,
что хотя бы одно из значений
следует,
что хотя бы одно из значений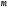 или
или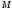 не принимается на концах отрезка
не принимается на концах отрезка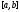 .
Пусть этим значением является
.
Пусть этим значением является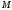 ,
т.е. существует такая точка
,
т.е. существует такая точка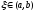 ,
что
,
что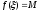 ,
и, значит, в этой точке
,
и, значит, в этой точке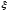 ф-я
ф-я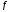 принимает наибольшее значение и на
интервале
принимает наибольшее значение и на
интервале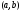 .
Поэтому из теоремы Ферма следует, что
.
Поэтому из теоремы Ферма следует, что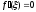 .Ч.т.д.
.Ч.т.д.
Геометрический
смысл: на
графике ф-ции найдется хотя бы одна
точка в интервале
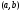 ,
касательная к графику в которой || оси
ОХ.
,
касательная к графику в которой || оси
ОХ.
Теорема
Лагранжа.
Если ф-я
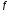 непрерывна
на отрезке
непрерывна
на отрезке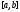 и в каждой точке интервала
и в каждой точке интервала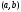 диф-ма, то в этом интервале существует
по крайней мере одна такая точка
диф-ма, то в этом интервале существует
по крайней мере одна такая точка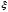 ,
что
,
что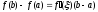 .
.
Геом.
смысл:
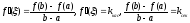 .
На
.
На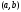 найдется точка, касательная к графику
ф-ции в кот. || секущей.
найдется точка, касательная к графику
ф-ции в кот. || секущей.
Теорема
Коши.
Пусть ф-и
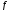 и
и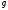 :
1) непрерывны на отрезке
:
1) непрерывны на отрезке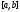 ;
2) имеют производные в каждой точке
интервала
;
2) имеют производные в каждой точке
интервала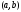 ;
3)
;
3)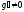 во
всех точках интервала
во
всех точках интервала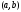 .
Тогда существует такая точка
.
Тогда существует такая точка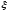 ,
,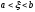 ,
что
,
что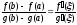 .
Заметим, что из условий теоремы следует,
что эта формула имеет смысл, т.е.
.
Заметим, что из условий теоремы следует,
что эта формула имеет смысл, т.е.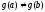 .
В самом деле, если
.
В самом деле, если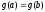 ,
то ф-я
,
то ф-я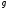 удовлетворяла
бы условиям теоремы Роля и, значит,
нашлась бы такая точка
удовлетворяла
бы условиям теоремы Роля и, значит,
нашлась бы такая точка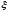 ,
что
,
что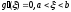 ,
что противоречило бы условию 3.
,
что противоречило бы условию 3.
Теорема
Дарбу:
если
производная дифференцируемой на отрезке
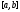 ф-ции принимает все значения между
ф-ции принимает все значения между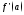 и
и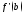 и на отрезке
и на отрезке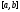 в ноль не обращается, то она на этом
отрезке сохраняет свой знак.
в ноль не обращается, то она на этом
отрезке сохраняет свой знак.
Следствие:
если
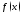 диф-ма на некот промежутке, то ее
производная на этом промежутке м. иметь
разрывы только второго рода.
диф-ма на некот промежутке, то ее
производная на этом промежутке м. иметь
разрывы только второго рода.
Правила Лопиталя.
Неопределенность
вида 0/0.
Теорема
1.
Пусть ф-и
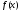 и
и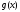 ,
определенны в некот. окрестности т.а,
,
определенны в некот. окрестности т.а,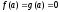 ,
существуют конечные производные
,
существуют конечные производные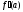 и
и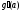 причем
причем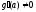 .
Тогда существует предел
.
Тогда существует предел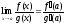 .
.
Теорема
2.
Пусть ф-и
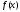 и
и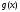 :
1) дифференцируемы на интервале
:
1) дифференцируемы на интервале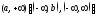 ;
2)
;
2)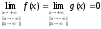 ;
3)
;
3)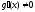 для всех
для всех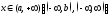 ;
4) существует конечный или бесконечный
предел
;
4) существует конечный или бесконечный
предел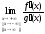 .
Тогда существует предел
.
Тогда существует предел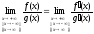 .
.
Неопределенность
вида
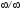 .
Теорема 1.
Пусть ф-и
.
Теорема 1.
Пусть ф-и
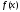 и
и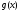 дифференцируемы в некот. окрестности
дифференцируемы в некот. окрестности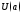 ,
,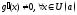 ,
,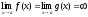 ,
существует конечный или бесконечный
предел
,
существует конечный или бесконечный
предел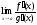 .
Тогда существует предел
.
Тогда существует предел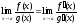 .
.
Теорема
2.
Пусть ф-и
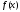 и
и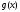 :
1) дифференцируемы на
:
1) дифференцируемы на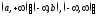 ,
2)
,
2)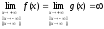 ;
3)
;
3)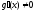 на
на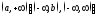 ;
4) существует конечный или бесконечный
предел
;
4) существует конечный или бесконечный
предел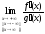 .
Тогда существует предел
.
Тогда существует предел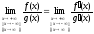 .
.
Условие монотонности дифференцируемости функций.
Теорема
1. Для
того чтобы дифференцируемая на интервале
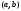 ф-я
ф-я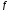 возрастала (убывала) на этом интервале
необходимо и достаточно, чтобы во всех
его точках производная была неотрицательной,
возрастала (убывала) на этом интервале
необходимо и достаточно, чтобы во всех
его точках производная была неотрицательной,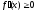 (соответственно, неположительной,
(соответственно, неположительной,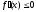 ).
Если всюду на
).
Если всюду на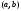 производная положительна:
производная положительна: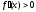 (соответственно отрицательна:
(соответственно отрицательна: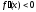 ),
то ф-я
),
то ф-я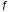 строго
возрастает (строго убывает) на
рассматриваемом интервале.
строго
возрастает (строго убывает) на
рассматриваемом интервале.
Точки экстремума функций.
Пусть
ф-я
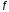 определена
в некоторой окрестности точки
определена
в некоторой окрестности точки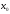 .
Тогда
.
Тогда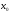 называется точкой максимума (соответственно
точкой минимума) ф-и
называется точкой максимума (соответственно
точкой минимума) ф-и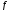 ,
если существует такое
,
если существует такое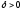 ,
что для всех
,
что для всех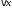 удовлетворяющих условию
удовлетворяющих условию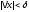 ,
выполняется неравенство
,
выполняется неравенство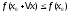 (соответственно
(соответственно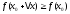 ).
Если существует такое
).
Если существует такое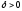 ,
что для всех
,
что для всех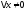 ,
таких, что
,
таких, что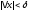 ,
выполняется неравенство
,
выполняется неравенство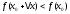 (соответственно
(соответственно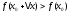 ,
то
,
то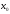 называется точкой строгого максимума
(соответственно строгого минимума).
Точки (строгого) максимума и минимума
называются точками (строгого) экстремума.
называется точкой строгого максимума
(соответственно строгого минимума).
Точки (строгого) максимума и минимума
называются точками (строгого) экстремума.
Теорема
2 (необходимые условия экстремума).
Пусть
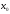 является точкой экстремума ф-и
является точкой экстремума ф-и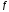 ,
определенной в некоторой окрестности
точки
,
определенной в некоторой окрестности
точки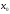 .
Тогда либо производная
.
Тогда либо производная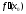 не существует, либо
не существует, либо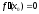 .
.
Теорема
3 (достаточные условия строгого
экстремума).
Пусть ф-я
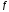 дифференцируема в некоторой окрестности
точки
дифференцируема в некоторой окрестности
точки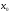 ,
кроме, быть может, самой точки
,
кроме, быть может, самой точки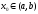 ,
в которой она является, однако,
непрерывной. Если производная
,
в которой она является, однако,
непрерывной. Если производная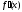 меняет
знак при переходе через
меняет
знак при переходе через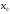 (это означает, что существует такое
число
(это означает, что существует такое
число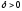 ,
что значения производной
,
что значения производной имеют один и тот же знак всюду в
имеют один и тот же знак всюду в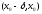 и противоположный знак для всех
и противоположный знак для всех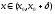 ),
то
),
то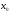 является точкой строгого экстремума.
При этом, если для
является точкой строгого экстремума.
При этом, если для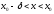 выполняется неравенство
выполняется неравенство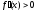 ,
а для
,
а для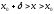 - неравенство
- неравенство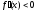 ,
то
,
то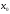 является точкой строгого максимума, а
если для
является точкой строгого максимума, а
если для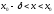 выполняется неравенство
выполняется неравенство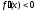 ,
а для
,
а для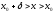 - неравенство
- неравенство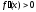 ,
то
,
то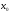 является точкой строгого минимума.
Если ф-я
является точкой строгого минимума.
Если ф-я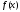 определена в некоторой окрестности
точки
определена в некоторой окрестности
точки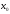 ,
непрерывна при
,
непрерывна при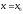 ,
имеет всюду в рассматриваемой окрестности
кроме, может быть, точки
,
имеет всюду в рассматриваемой окрестности
кроме, может быть, точки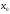 ,
производную и эта производная с каждой
стороны от
,
производную и эта производная с каждой
стороны от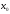 сохраняет
постоянный знак (следовательно, можно
говорить о сохранении или перемене
знака у производной при переходе через
сохраняет
постоянный знак (следовательно, можно
говорить о сохранении или перемене
знака у производной при переходе через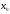 ),
то для того чтобы при
),
то для того чтобы при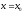 ф-я достигала экстремума необходимо и
достаточно, чтобы производная меняла
знак при переходе через точку
ф-я достигала экстремума необходимо и
достаточно, чтобы производная меняла
знак при переходе через точку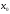 .
.
Условие выпуклости графика ф-и.
Ф-я
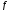 называется выпуклой вверх (выпуклой
вниз) на интервале
называется выпуклой вверх (выпуклой
вниз) на интервале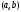 ,
если каковы бы ни были точки
,
если каковы бы ни были точки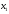 и
и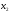 ,
,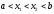 ,
для любой точки
,
для любой точки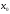 интервала
интервала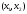 ,
выполняется неравенство
,
выполняется неравенство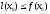 ,
(соответственно
,
(соответственно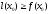 ),
где
),
где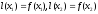 .
Если выполняются строгие неравенства
.
Если выполняются строгие неравенства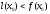 и
и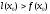 при
любых
при
любых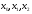 таких, что
таких, что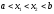 ,
то ф-я
,
то ф-я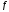 называется
строго выпуклой вверх (строго выпуклой
вниз) на интервале
называется
строго выпуклой вверх (строго выпуклой
вниз) на интервале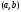 .
Всякий интервал, на котором ф-я (строго)
выпукла вверх, соответственно вниз,
называется интервалом (строгой)
выпуклости вверх, соответственно вниз,
этой ф-и.
.
Всякий интервал, на котором ф-я (строго)
выпукла вверх, соответственно вниз,
называется интервалом (строгой)
выпуклости вверх, соответственно вниз,
этой ф-и.
Теорема
(достаточное условие строгой выпуклости).
Пусть ф-я
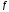 дважды
дифференцируема на интервале
дважды
дифференцируема на интервале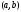 .
Тогда, если
.
Тогда, если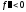 на
на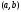 ,
то ф-я
,
то ф-я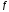 строго
выпукла вверх, а если
строго
выпукла вверх, а если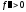 на
на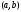 ,
то ф-я
,
то ф-я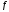 строго выпукла вниз на этом интервале.
строго выпукла вниз на этом интервале.
Точки перегиба.
Пусть
ф-я
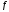 дифференцируема при
дифференцируема при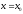 и пусть
и пусть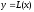 -
уравнение касательной к графику ф-и
-
уравнение касательной к графику ф-и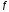 в точке
в точке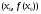 .
Если разность
.
Если разность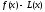 меняет знак при переходе через точку
меняет знак при переходе через точку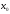 ,
то
,
то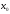 называется точкой перегиба ф-и
называется точкой перегиба ф-и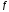 .
.
Асимптоты.
Пусть
ф-я
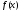 определена
для всех
определена
для всех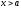 (соответственно
для всех
(соответственно
для всех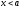 ).
Если существуют такие числа
).
Если существуют такие числа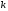 и
и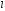 ,
что
,
что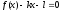 при
при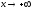 (соответственно при
(соответственно при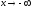 ),
то прямая
),
то прямая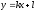 называется асимптотой графика ф-и
называется асимптотой графика ф-и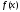 при
при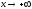 (соответственно при
(соответственно при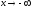 ). Пусть ф-я
). Пусть ф-я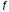 определена в некоторой окрестности
точки
определена в некоторой окрестности
точки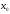 (быть может, односторонней) и пусть
выполнено хотя бы одно из условий
(быть может, односторонней) и пусть
выполнено хотя бы одно из условий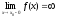 ,
или
,
или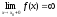 .
Тогда прямая
.
Тогда прямая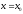 называется вертикальной асимптотой
графика ф-и
называется вертикальной асимптотой
графика ф-и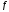 .
.
Общая схема построения графика функции.
1.Определить область существования ф-и, область непрерывности и точки разрыва. 2. Найти асимптоты. 3. Приблизительно нарисовать график ф-и. 4. Вычислить первую, а если нужно, и вторую производную. 5. Найти точки, в которых первая и вторая производные либо не существуют, либо равны нулю. 6. Составить таблицу изменения знака первой и второй производных. Определить промежутки возрастания, убывания, выпуклости вверх или вниз ф-и, найти точки экстремума (в том числе концевые) и точки перегиба. 7. Окончательно вычертить график.
Исследование графиков ф-и.
Пусть
ф-я
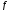 определена в некоторой окрестности
точки
определена в некоторой окрестности
точки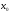 .
Будем называть
.
Будем называть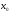 точкой возрастания (убывания) ф-и
точкой возрастания (убывания) ф-и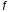 ,
если существует такое
,
если существует такое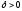 ,
что при
,
что при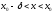 выполняется неравенство
выполняется неравенство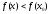 (соответственно
(соответственно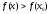 ),
а при
),
а при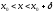 - неравенство
- неравенство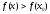 (соответственно
(соответственно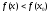 ).
).
