
- •5. Линейное пространство. Евклидово и унитарное пространства
- •6. Линейные операторы и их свойства
- •Линейные преобразования евклидова пространства
- •7. Действительные числа. Функция действительной переменной. Предел функции. Непрерывные функции.
- •8. Производная и дифференциал. Производные и дифференциалы высших порядков. Формула Тейлора
- •9. Основные теоремы дифференциального исчисления и их применения
- •10. Первообразная и неопределенный интеграл
- •4. Интегрирование некоторых тригонометрических функций.
- •6. Интеграл вида если функцияR является нечетной относительно cosx.
- •11. Определенный интеграл Римана, его свойства. Применения к вычислению геометрических, физических и механических величин Определенный интеграл
- •12. Функции нескольких действительных переменных.
- •13. Частные производные и дифференцируемость ф-ции в точке. Производные и дифференциалы высших порядков. Равенство смешанных производных
- •14. Неявная и обратная функции. Экстремумы
- •15. Числовые ряды и их сходимость.
- •16. Функциональные последовательности и ряды. Степенные ряды. Ряд Тейлора.
- •2) Дифференцирование степенных рядов.
- •3) Сложение, вычитание, умножение и деление степенных рядов.
- •18. Ряды Фурье. Преобразование Фурье. Интеграл Фурье
- •Разложение в ряд Фурье четных и нечетных функций
- •Разложение в ряд Фурье функций произвольного периода
- •Представление непериодической функции ряда Фурье
- •Тригонометрический ряд Фурье в комплексной области
- •Свойства ряда Фурье
- •- Неравенство Бесселя.
- •- Равенство Парсеваля,
- •Понятие об интеграле Фурье и об преобразовании Фурье
- •19. Мера Лебега, измеримые множества и функции
- •20. Интеграл Лебега и его свойства.
- •21. Ф-ции комплексной переменной. Диф-ние и инт-ние. Теорема Коши.
- •22. Ряды Тейлора и Лорана. Вычеты
- •Аналитические функции и их разложение в степенные ряды.
- •Свойства максимума модуля аналитических и гармонических функций.
- •Ряд Тейлора.
- •Ряд Лорана.
- •Изолированные особые точки аналитических функций и их классификация.
- •Вычеты и основная теорема о вычетах.
- •Применение к вычислению интегралов.
- •23. Математическое моделирование и вычислительный эксперимент
- •24. Численные методы в алгебре
- •Обусловленность систем линейных алгебраических уравнений
- •Вычисление определителей и обращение матриц
- •Итерационные методы
- •Достаточное условие сходимости итерационного процесса
- •25. Решение нелинейных уравнений и систем уравнений
- •26. Приближение функций.
- •27. Численное дифференцирование. Численное интегрирование
- •28. Решение обыкновенного дифференциального уравнения первого порядка методами Эйлера, Эйлера – Коши, Рунге – Кутты. Метод конечных разностей.
- •29. Разностные методы решения задач математической физики.
- •33. Линейные уравнения и системы.
- •34.Линейные уравнения и системы с постоянными коэффициентами
- •35. Устойчивость решений дифференциальных уравнений
- •Простейшие типы точек покоя. Автономные динамические системы двух уравнений первого порядка. Типы особых точек на фазовой плоскости
- •№37 Физические задачи, приводящие к уравнению параболического типа
- •Интеграл Пуассона
- •39. Алгебра логики
- •3. Основные законы логики.
- •4. Логические функции.
- •5. Нормальные формы. Совершенные нормальные формы.
- •Алгоритм построения сднф.
- •6. Арифметические операции в алгебре логики. Полином Жегалкина.
- •7. Полнота и замкнутость (примеры полных систем). Теорема Поста.
- •Свойства отношений.
- •40. Графы и их свойства
- •41. Маршруты в графах и деревья
- •41. Маршруты в графах и деревья
Линейные преобразования евклидова пространства
Нормальный оператор
 (если
сопряженный совпадает с обратным) или
(если
сопряженный совпадает с обратным) или

Пример:

 ,
,
 -
норм.
-
норм.
Ортогональные операторы
Линейный
оператор
![]() называется
ортогональным, если
называется
ортогональным, если
![]()
Для
того чтобы оператор
![]() был
ортогональным, необходимо и достаточно,
чтобы его матрица в ортонормированном
базисе была ортогональной.
был
ортогональным, необходимо и достаточно,
чтобы его матрица в ортонормированном
базисе была ортогональной.
Ортогональные операторы и только они сохраняют длину вектора, т. е.
![]()
Сопряженные операторы
Оператор
![]() называется
сопряженным линейному оператору
называется
сопряженным линейному оператору![]() ,
если
,
если
![]()
Оператор
 также
является линейным оператором. Еслиf
в некотором ортогональном базисе имеет
матрицу A,
то в этом базисе оператор
также
является линейным оператором. Еслиf
в некотором ортогональном базисе имеет
матрицу A,
то в этом базисе оператор
 имеет
матрицу
имеет
матрицу .
.
Свойства
сопряженных операторов:
![]()
![]()
![]()
![]()
![]() (f
- невырожденный).
(f
- невырожденный).
Самосопряженные операторы
Линейный
оператор
![]() называется
самосопряженным (симметрическим), если
называется
самосопряженным (симметрическим), если
![]()
Для
самосопряженного оператора
 .
Оператор
.
Оператор![]() является
самосопряженным тогда и только тогда,
когда его матрица в некотором
ортонормированном базисе симметрическая.
является
самосопряженным тогда и только тогда,
когда его матрица в некотором
ортонормированном базисе симметрическая.
Свойства самосопряженных операторов: 1) самосопряженный оператор имеет только действительные собственные числа; 2) всякий самосопряженный оператор является оператором простой структуры; 3) для всякого самосопряженного оператора существует ортонормированный базис, состоящий из собственных векторов этого оператора.
Самосопряжённый оператор - совпадающий со своим сопряжённым иначе называется эрмитовым.
Комплексное
линейное пространство называется
унитарным
пространством
 .
.
 называется унитарным
оператором, если он сохраняет скалярное
произведение векторов (сохраняется
длина векторов).
называется унитарным
оператором, если он сохраняет скалярное
произведение векторов (сохраняется
длина векторов).
Док-во:
 - ортонормированная база,
- ортонормированная база, ,
, .
.
 ,
,
 ,
, .
Если
.
Если ,
то
,
то длина
вектора после действия оператора
сохраняется.
длина
вектора после действия оператора
сохраняется.
7. Действительные числа. Функция действительной переменной. Предел функции. Непрерывные функции.
Система,
состоящая из всех рациональных
 (все числа вида
(все числа вида )
и всех иррациональных
)
и всех иррациональных (все бесконечные непериодические
десятичные дроби) чисел, называется
системойдействительных
(вещественных) чисел
(все бесконечные непериодические
десятичные дроби) чисел, называется
системойдействительных
(вещественных) чисел
 .
.
Свойства действительных чисел:
 -
определена операция сложения
-
определена операция сложения
 -
коммутативность сложения;
-
коммутативность сложения; -
ассоциативность сложения;
-
ассоциативность сложения; -
св-во нуля;
-
св-во нуля; -
св-во противоположного числа
-
св-во противоположного числа
Выполнение
этих св-тв означает, что
 - абелева (коммутативная) группа по
сложению.
- абелева (коммутативная) группа по
сложению.
 -
определена операция умножения
-
определена операция умножения
 -
коммутативность умножения;
-
коммутативность умножения; -
ассоциативность умножения;
-
ассоциативность умножения; -
св-во единицы;
-
св-во единицы; -
св-во обратного элемента.
-
св-во обратного элемента.
 -
абелева группа по умножению.
-
абелева группа по умножению.
 -
св-во дистрибутивности
-
св-во дистрибутивности
 -
св-во рефлексивности;
-
св-во рефлексивности; -
з-н тождества;
-
з-н тождества; -
св-во транзитивности.
-
св-во транзитивности.
 -
линейно-упорядоченное множество.
-
линейно-упорядоченное множество.
 -
св-во сохранения неравенства;
-
св-во сохранения неравенства; -
з-н сохранения знаков.
-
з-н сохранения знаков.
Th. Архимеда: для
 .
.Th. Дедекинда (о св-ве полноты или непрерывности мн-ва
 )
)

]
 - два произвольных множества.
- два произвольных множества.
]
 поставлен в соответствие один и только
один
поставлен в соответствие один и только
один .
Тогда это соответствие называетсяфункцией
с областью определения
.
Тогда это соответствие называетсяфункцией
с областью определения
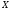 и областью значений, лежащей в
и областью значений, лежащей в .
.
Свойства функций:
Ф-я наз. строговозрастающей (возрастающей) на мн-ве
 ,
если большему значению аргумента
соответствует большее значение ф-ции.
,
если большему значению аргумента
соответствует большее значение ф-ции.

Ф-я
наз. возрастающей
(неубывающей)
на мн-ве
 ,
если большему значению аргумента
соответствует неменьшее значение
ф-ции.
,
если большему значению аргумента
соответствует неменьшее значение
ф-ции.

Ф-я
наз. строгоубывающей
(убывающей)
на мн-ве
 ,
если большему значению аргумента
соответствует меньшее значение ф-ции.
,
если большему значению аргумента
соответствует меньшее значение ф-ции.

Ф-я
наз. убывающей
(невозрастающей)
на мн-ве
 ,
если большему значению аргумента
соответствует небольшее значение
ф-ции.
,
если большему значению аргумента
соответствует небольшее значение
ф-ции.

Все эти ф-ции наз-ся монотонными.
Ф-я
 наз-сячетной,
если
наз-сячетной,
если
мн-во
 симметрично относительно начала
координат;
симметрично относительно начала
координат;
 .
.
Ф-я
 наз-сянечетной,
если
наз-сянечетной,
если
мн-во
 симметрично относительно начала
координат;
симметрично относительно начала
координат;
 .
.
Ф-я
 наз-сяпериодической
на мн-ве
наз-сяпериодической
на мн-ве
 ,
если
,
если ,
что
,
что и
и .
Число
.
Число наз-ся периодом ф-ции.
наз-ся периодом ф-ции.Ф-я
 ,
опр-ная на мн-веX
наз-ся ограниченной
сверху (снизу),
если мн-во ее значений ограничено
сверху (снизу).
,
опр-ная на мн-веX
наз-ся ограниченной
сверху (снизу),
если мн-во ее значений ограничено
сверху (снизу).

M(m)
–верхняя
(нижняя) граница ф-ции
 на множествеX.
на множествеX.
Ф-я
 наз-сяограниченной
на мн-ве
наз-сяограниченной
на мн-ве
 ,
если
,
если


 .
Это опр-е
.
Это опр-е



 .
.
Наименьшая
из верхних границ наз-ся верхней гранью
ф-ции

 .
.
Наибольшая
из нижних границ наз-ся нижней гранью
ф-ции

 .
.
Ф-я наз-ся неограниченной, если она не ограничена ни сверху, ни снизу.
Определение предела функции:
Точка
 называетсяпредельной
точкой мн-ва
называетсяпредельной
точкой мн-ва
 ,
если в
,
если в окрестности т.
окрестности т. найдутся точки мн-ва
найдутся точки мн-ва ,
отличные от
,
отличные от .
.
общее определение (на языке окрестностей):
Число
 наз-ся пределом ф-ции
наз-ся пределом ф-ции при
при ,
если для
,
если для окрестности
окрестности точки
точки найдется такая окрестность
найдется такая окрестность точки
точки ,
что для всех
,
что для всех из
из значение
значение .
.
 .
.
по Коши (на языке
 ):
):
]
 (аналогично формулируется опр-е предела
для
(аналогично формулируется опр-е предела
для других
других и
и )
)
 .
.
по Гейне:
Число
 называется пределом функции
называется пределом функции при
при ,
если для любой последовательности
,
если для любой последовательности
 последовательность
последовательность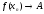 ,
т.е.
,
т.е.
Th: Определение предела функции по Гейне эквивалентно определению предела функции по Коши.
Элементарные свойства предела:
Th. о единственности предела.
Если функция имеет предел, то этот предел единственный.
Th. о локальной ограниченности ф-ции, имеющей конечный предел.
Если
ф-я имеет конечный предел в точке
 ,
то в некоторой проколотой окрестности
этой точки ф-я ограничена.
,
то в некоторой проколотой окрестности
этой точки ф-я ограничена.
Док-во:



 ограничена
в
ограничена
в
 ч.т.д.
ч.т.д.
Th. о сохранении ф-цией знака своего предела.
]
предел ф-ции
 при
при равен
равен и
и .
Тогда в некоторой проколотой окрестности
точки
.
Тогда в некоторой проколотой окрестности
точки значения ф-ции положительны (отрицательны).
значения ф-ции положительны (отрицательны).
Основные свойства предела:
Th. Критерий
 -ния
предела.
-ния
предела.
Для
того, чтобы
 конечный предел
конечный предел н. и д., чтобы
н. и д., чтобы была бесконечно малой величиной в точке
была бесконечно малой величиной в точке .
.
Th. О пределе суммы, произведения и частного.
]
 -ют
конечные пределы:
-ют
конечные пределы: и
и .
Тогда
.
Тогда


 при
при
 .
.
Докажем
 :
:
 ,
,
 - б.м. в т.
- б.м. в т. .
.

 -
б.м. в т.
-
б.м. в т.
 .
.
 ч.т.д.
ч.т.д.
Th. о предельном переходе в неравенстве.
Если
 и
и ,
в некоторой проколотой окрестности
точки
,
в некоторой проколотой окрестности
точки выполняется неравенство
выполняется неравенство ,
то в этой окрестности выполняется
неравенство
,
то в этой окрестности выполняется
неравенство .
.
Th. о пределе промежуточной функции.
]
даны ф-ции
 ,
, .
Тогда
.
Тогда .
.
]
 опр-на на мн-ве
опр-на на мн-ве ,
мн-во
,
мн-во ,
, - предельная т. мн-ва
- предельная т. мн-ва .
.

Th.
Если мн-во
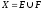 ,
то
,
то .
Иначе: предел в т.
.
Иначе: предел в т.
 и равен
и равен ,
т. и т. т., к.
,
т. и т. т., к. пределы по мн-вам
пределы по мн-вам и
и в т.
в т. и эти пределы совпадают с
и эти пределы совпадают с .
.
Пусть
функция
 задана на мн-ве
задана на мн-ве и
и -
предельная точка этого множества.
Функция называетсянепрерывной
в точке
-
предельная точка этого множества.
Функция называетсянепрерывной
в точке
 ,
если предел функции в этой точке равен
ее значению, т.е.
,
если предел функции в этой точке равен
ее значению, т.е.

Функция,
непрерывная в каждой точке множества
 ,
называетсянепрерывной
на множестве
,
называетсянепрерывной
на множестве

Th:
Если функции
 и
и непрерывны
в точке
непрерывны
в точке ,
то в точке
,
то в точке непрерывны
функции
непрерывны
функции .
.
Функция
 называется
непрерывной слева (справа) в точке
называется
непрерывной слева (справа) в точке ,
если
,
если (
( ).
).
Th:
]
 левый и правый пределы функции
левый и правый пределы функции в точке
в точке .
Для непрерывности функции
.
Для непрерывности функции в точке
в точке н.
и д., ч. функция в этой точке была
непрерывна слева и справа.
н.
и д., ч. функция в этой точке была
непрерывна слева и справа.
Классификация точек разрыва:
Пусть
 опр-на на
опр-на на и
и .
Точка
.
Точка называетсяточкой
разрыва
функции
называетсяточкой
разрыва
функции
 ,
если в этой точке ф-ция не является
непрерывной в этой точке. Изолированная
точка не м.б. точкой разрыва.
,
если в этой точке ф-ция не является
непрерывной в этой точке. Изолированная
точка не м.б. точкой разрыва.
 ,
но
,
но
 .
Тогда т.
.
Тогда т. - т.разрываI
рода, разрыв ф-ции устраним.
- т.разрываI
рода, разрыв ф-ции устраним. .
Тогда т.
.
Тогда т.
 - т.разрываI
рода, разрыв ф-ции неустраним.
- т.разрываI
рода, разрыв ф-ции неустраним.Хотя бы один из односторонних пределов не существует или равен бесконечности. Тогда т.
 - т.разрываII
рода, разрыв ф-ции неустраним.
- т.разрываII
рода, разрыв ф-ции неустраним.
Функция
называется
 непрерывной
на отрезке
непрерывной
на отрезке
 (на множестве точек
(на множестве точек ,
удовлетворяющих неравенствам
,
удовлетворяющих неравенствам ),
если она непрерывна в точках интервала
),
если она непрерывна в точках интервала (мн-во точек
(мн-во точек ,
для которых
,
для которых ),
непрерывна справа в точке
),
непрерывна справа в точке и
непрерывна слева в точке
и
непрерывна слева в точке .
.
Свойства непрерывных функций на отрезке:
Th: Если функция
 непрерывной
на отрезке
непрерывной
на отрезке
 ,
то она ограничена на нем.
,
то она ограничена на нем.Th: Непрерывная на
 функция
функция достигает
в некоторых точках отрезка
достигает
в некоторых точках отрезка своих максимума и минимума, т.е.
существуют точки
своих максимума и минимума, т.е.
существуют точки и
и ,
принадлежащие
,
принадлежащие ,
для которых имеет место
,
для которых имеет место ,
, .
Т.о.,
.
Т.о., для всех
для всех .
.Th: Если функция
 явл. непрерывной
на отрезке
явл. непрерывной
на отрезке
 и числа
и числа и
и не
равны нулю и имеют разные знаки, то на
интервале
не
равны нулю и имеют разные знаки, то на
интервале имеется по крайней мере одна точка
имеется по крайней мере одна точка такая,
что
такая,
что
Если
функция
 явл. непрерывной
на
явл. непрерывной
на
 ,
, и
и -
произвольное число, находящееся между
числами
-
произвольное число, находящееся между
числами и
и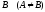 ,
то на интервале
,
то на интервале найдется, по крайней мере, одна точка
найдется, по крайней мере, одна точка ,
для которой
,
для которой
Теоремы о промежуточных значениях непрерывных функций.
Первая теорема Больцано-Коши.
Если
ф-я
 опр-на и непр-на на отрезке
опр-на и непр-на на отрезке и на концах отрезка принимает значения
разных знаков, то м/у точками
и на концах отрезка принимает значения
разных знаков, то м/у точками и
и
 ,
такая, что
,
такая, что .
.
Док-во:
Делим
 пополам. Выбираем тот отрезок, в левом
конце которого ф-я принимает отриц.
значение, а в правом – положительное,
обозначим
пополам. Выбираем тот отрезок, в левом
конце которого ф-я принимает отриц.
значение, а в правом – положительное,
обозначим .
Если оказалось, что в точке деления ф-я
равна нулю, то ч.т.д.
.
Если оказалось, что в точке деления ф-я
равна нулю, то ч.т.д.
Делим
 пополам. Если в точке деления ф-я равна
нулю, то ч.т.д. Если нет, то делаем
описанную выше процедуру.
пополам. Если в точке деления ф-я равна
нулю, то ч.т.д. Если нет, то делаем
описанную выше процедуру.
В
итоге получим посл-ть вложенных отрезков:
 .
.


По
принципу вложенных отрезков
 .
.
 ч.т.д.
ч.т.д.
Вторая теорема Больцано-Коши.
Если
ф-я
 опр. и непр. на отр.
опр. и непр. на отр.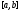 и на концах этого отрезка принимает
разные значения
и на концах этого отрезка принимает
разные значения ,
то для
,
то для

 .
.
Первая теорема Вейерштрасса.
Непрерывная на отрезке функция ограничена.
Вторая теорема Вейерштрасса.
Непрерывная на отрезке функция принимает на этом отрезке свои наибольшее и наименьшее значения.
В данных теоремах отрезок нельзя заменить интервалом или полуинтервалом.
Теорема Кантора.
Функция, непрерывная на отрезке, равномерно непрерывна на этом отрезке.
Функция
 называетсяравномерно
непрерывной на
называетсяравномерно
непрерывной на
 ,
если
,
если такое, что
такое, что
Из
равномерной непрерывности функции на
 ,
очевидно, следует её непрерывность в
каждой точке множества
,
очевидно, следует её непрерывность в
каждой точке множества .
Обратное неверно.
.
Обратное неверно.
Функция, непрерывная на отрезке, равномерно непрерывна на этом отрезке.
Если
для
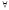 различных элементов
различных элементов и
и из
из ф-я ставит в соот-вие два различных
эл-та
ф-я ставит в соот-вие два различных
эл-та и
и из
из ,
то ф-я
,
то ф-я наз-ся инъекцией. При этом условии ф-я
наз-ся инъекцией. При этом условии ф-я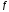 имеет обратную ф-ю, причем она также
будет инъекцией.
имеет обратную ф-ю, причем она также
будет инъекцией.
Th.
Если ф-я
 строго возрастает (убывает) и непрерывна
в некот. промежутке
строго возрастает (убывает) и непрерывна
в некот. промежутке ,
то в соот-щем промежутке
,
то в соот-щем промежутке ее значений
ее значений обратная ф-я
обратная ф-я
 ,
кот. непр. и строго возр. (убывает).
,
кот. непр. и строго возр. (убывает).
 .
.
Th.
] ф-я
 непр в т.
непр в т. ,
а ф-я
,
а ф-я непр. в т.
непр. в т. .
Тогда сложная ф-я
.
Тогда сложная ф-я непр. в т.
непр. в т. .
.
Число e.

