
- •5. Линейное пространство. Евклидово и унитарное пространства
- •6. Линейные операторы и их свойства
- •Линейные преобразования евклидова пространства
- •7. Действительные числа. Функция действительной переменной. Предел функции. Непрерывные функции.
- •8. Производная и дифференциал. Производные и дифференциалы высших порядков. Формула Тейлора
- •9. Основные теоремы дифференциального исчисления и их применения
- •10. Первообразная и неопределенный интеграл
- •4. Интегрирование некоторых тригонометрических функций.
- •6. Интеграл вида если функцияR является нечетной относительно cosx.
- •11. Определенный интеграл Римана, его свойства. Применения к вычислению геометрических, физических и механических величин Определенный интеграл
- •12. Функции нескольких действительных переменных.
- •13. Частные производные и дифференцируемость ф-ции в точке. Производные и дифференциалы высших порядков. Равенство смешанных производных
- •14. Неявная и обратная функции. Экстремумы
- •15. Числовые ряды и их сходимость.
- •16. Функциональные последовательности и ряды. Степенные ряды. Ряд Тейлора.
- •2) Дифференцирование степенных рядов.
- •3) Сложение, вычитание, умножение и деление степенных рядов.
- •18. Ряды Фурье. Преобразование Фурье. Интеграл Фурье
- •Разложение в ряд Фурье четных и нечетных функций
- •Разложение в ряд Фурье функций произвольного периода
- •Представление непериодической функции ряда Фурье
- •Тригонометрический ряд Фурье в комплексной области
- •Свойства ряда Фурье
- •- Неравенство Бесселя.
- •- Равенство Парсеваля,
- •Понятие об интеграле Фурье и об преобразовании Фурье
- •19. Мера Лебега, измеримые множества и функции
- •20. Интеграл Лебега и его свойства.
- •21. Ф-ции комплексной переменной. Диф-ние и инт-ние. Теорема Коши.
- •22. Ряды Тейлора и Лорана. Вычеты
- •Аналитические функции и их разложение в степенные ряды.
- •Свойства максимума модуля аналитических и гармонических функций.
- •Ряд Тейлора.
- •Ряд Лорана.
- •Изолированные особые точки аналитических функций и их классификация.
- •Вычеты и основная теорема о вычетах.
- •Применение к вычислению интегралов.
- •23. Математическое моделирование и вычислительный эксперимент
- •24. Численные методы в алгебре
- •Обусловленность систем линейных алгебраических уравнений
- •Вычисление определителей и обращение матриц
- •Итерационные методы
- •Достаточное условие сходимости итерационного процесса
- •25. Решение нелинейных уравнений и систем уравнений
- •26. Приближение функций.
- •27. Численное дифференцирование. Численное интегрирование
- •28. Решение обыкновенного дифференциального уравнения первого порядка методами Эйлера, Эйлера – Коши, Рунге – Кутты. Метод конечных разностей.
- •29. Разностные методы решения задач математической физики.
- •33. Линейные уравнения и системы.
- •34.Линейные уравнения и системы с постоянными коэффициентами
- •35. Устойчивость решений дифференциальных уравнений
- •Простейшие типы точек покоя. Автономные динамические системы двух уравнений первого порядка. Типы особых точек на фазовой плоскости
- •№37 Физические задачи, приводящие к уравнению параболического типа
- •Интеграл Пуассона
- •39. Алгебра логики
- •3. Основные законы логики.
- •4. Логические функции.
- •5. Нормальные формы. Совершенные нормальные формы.
- •Алгоритм построения сднф.
- •6. Арифметические операции в алгебре логики. Полином Жегалкина.
- •7. Полнота и замкнутость (примеры полных систем). Теорема Поста.
- •Свойства отношений.
- •40. Графы и их свойства
- •41. Маршруты в графах и деревья
- •41. Маршруты в графах и деревья
Тригонометрический ряд Фурье в комплексной области


 ,
,


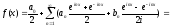






 -
это комплексная форма комплексного
ряда Фурье.
-
это комплексная форма комплексного
ряда Фурье.
[-l,
l]


 .
.
Свойства ряда Фурье
Пусть
дан ряд Фурье:

Справедлива теорема:
Для
любой ортонормированной системы en
и любой функции f(x)
c
условием
 справедливо неравенство:
справедливо неравенство:
- Неравенство Бесселя.
Это
условие означает, что ряд из коэффициентов
Фурье сходится по метрике
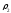 .
Если выполняется равенство:
.
Если выполняется равенство:
- Равенство Парсеваля,
в этом случае ортонормированная система en – замкнута.
Из
этого равенства =>
 - это означает, что ряд сходится к суммеf.
- это означает, что ряд сходится к суммеf.

Опр. Система en называется полной в l2, если множество линейных комбинаций функций этой системы плотно в l2, т.е. замыкание этого множества совпадает с множеством l2.
Теорема:
Полнота системы en равносильна выполнению равенства Парсеваля для любых f из l2.
Теорема:
Если функция гладкая, то ряд Фурье сходится равномерно к этой функции.
Понятие об интеграле Фурье и об преобразовании Фурье
Интеграл Фурье имеет вид:

несобственные интегралы понимаются в смысле главного значения:
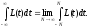
функция
вида
 -преобразование
Фурье функции
f(x).
-преобразование
Фурье функции
f(x).
Функцию F(x) называют обратным преобразованием Фурье функции g(x).
Замечание: Как правило, F(x) = f(x).
Часто
в преобразовании Фурье вместо 1 берут
 ,
вместо
,
вместо -
- .
.
Свойства:
Если
 ,
тоg(y)
непрерывно на
,
тоg(y)
непрерывно на

Если
 ,
то
,
то при
при .
.Если
 и в некоторой δ-окрестности точкаx0
(δ(x0))
имеет ограниченную вариацию, то F(x0)
= f(x0).
и в некоторой δ-окрестности точкаx0
(δ(x0))
имеет ограниченную вариацию, то F(x0)
= f(x0).Если
 ,
то преобразование Фурье имеетk-производных.
,
то преобразование Фурье имеетk-производных.
Теорема: (Равенство Планшереля)
Пусть
дано

 φ
φ



 преобразование Фурье дляf(x)
и для φ(x);
преобразование Фурье дляf(x)
и для φ(x);
тогда справедливо равенство:

19. Мера Лебега, измеримые множества и функции
Мера-аналог длины.
Элементарным множеством наз. множество, которые можно представить в виде (хотя бы одним способом) объединения попарно не пересекающихся прямоугольников. мера прямоугольника — это его площадь.
 ,
An
—
прямоугольники,
,
An
—
прямоугольники,
 — мера элементарных множеств, где
— мера элементарных множеств, где — площадь прямоугольника.
— площадь прямоугольника.
Если А и В – элементарные множества, то А U В, А ∩В, А \ В, А ∆ В (симметричная разность) тоже элементарные.
Пусть А –неэлементарное множество, произвольное ограниченное множество. Тогда выбирают покрытие конечным числом прямоугольников и вводят понятие внешней меры.
Внешней
мерой множества А
называется число
 ,
гдеPk
–покрытие.
,
гдеPk
–покрытие.
Если
А — элементарное мн-во, то

Теорема.
Если
 ,
то
,
то
Множество А называется измеримым в смысле Лебега, если для

 В:|
В:|
 (А Δ В=(А\В)
(А Δ В=(А\В) (В/А)),
т.е. внешняя мера сим. разности А иB
меньше ε
(В/А)),
т.е. внешняя мера сим. разности А иB
меньше ε
Функция
 ,
рассматриваемая на измеримых в смысле
Лебега множествах, называется лебеговой
мерой:
,
рассматриваемая на измеримых в смысле
Лебега множествах, называется лебеговой
мерой: .
.
Множество измеримо, если его можно сколь угодно точно приблизить к элементарным множествам.
Теоремы об измеримых множествах
1) Дополнение измеримого множества измеримо
2) Объединение или пересечение конечного числа измеримых множеств измеримо.
3) Разность и симметричная разность двух измеримых множеств измеримы.
4)
Если А1,…,Аn
попарно непересекающиеся измеримые
множества, то

5)
Если А – измеримо, то его мера считается
следующим образом (Е — универсальное
мн-во):
6) Сумма и пересечение счетного числа измеримых множеств есть измеримое множество.
7)
Счетная аддитивность ( –аддитивность)меры:
ЕслиA1,…,An,…–
попарно непересекающиеся измеримые
множества, то
–аддитивность)меры:
ЕслиA1,…,An,…–
попарно непересекающиеся измеримые
множества, то

8)
Из счетной аддитивности мер следует
непрерывность меры: если

 ,
то
,
то
9)
Если А1 ….
…. Аn
Аn …
т.е.
…
т.е.
 ,
то
,
то
Определение:
Множество
 наз множеством меры нуль, если для
каждого ε > 0 сущ. конечная или счетная
система отрезков {[αn,
βn]}
такая, что: 1. мн-во М покрывается
отрезками этой с-мы, т.е.
наз множеством меры нуль, если для
каждого ε > 0 сущ. конечная или счетная
система отрезков {[αn,
βn]}
такая, что: 1. мн-во М покрывается
отрезками этой с-мы, т.е.
 2. сумма длин отрезков {[αn,
βn]}<
ε,
т.е.
2. сумма длин отрезков {[αn,
βn]}<
ε,
т.е.
 .
Примером мн-ва меры нуль явл. мн-во
рациональных чисел:
.
Примером мн-ва меры нуль явл. мн-во
рациональных чисел:
Д-во:
рац. числа отрезка [a,
b]
образуют счетное мн-во, т.е. их можно
занумеровать: r1,…rn,….
Тогда для данного ε > 0 и каждого рац.
числа rn
построим отрезок
 1)
1) 2)
2) ,
т.е. согласно определению мн-во
,
т.е. согласно определению мн-во —
мн-во меры нуль.
—
мн-во меры нуль.
Примеры: 1) всякое огранич. множество А, внешняя мера которого равна 0, измерима. При этом выполняется равенство:

2) Всякое подмножество множества меры нуль измеримо и его мера равна нулю.
3) Всякое ограниченное, не более чем счетное множество измеримо и его мера равна нулю.
4) Мера ограниченного открытого мн-ва — это сумма длин составляющих его интервалов, т.е. оно измеримо.
Замкнутое ограниченное мн-во измеримо как дополнение измеримого мн-ва.
Любое измеримое множество с положительной лебеговой мерой содержит неизмеримое подмножество.
Измеримые функции
Пусть
функция
 задана
на множествеE.
задана
на множествеE.
Функция
 называется измеримой на этом множестве,
если измеримы для любых действительных
называется измеримой на этом множестве,
если измеримы для любых действительных множества:
множества:
 ={x
={x E,
f(x)>a},
E,
f(x)>a}, ,
, ,
,
Замечание: Достаточно потребовать измеримости одного из четырех множеств.
Две
функции
 и
и ,
заданные на множестве Е, называются
равными почти всюду на Е (эквивалентные
на Е)f
~ g,
если множество точек Е, в кот.
,
заданные на множестве Е, называются
равными почти всюду на Е (эквивалентные
на Е)f
~ g,
если множество точек Е, в кот.
 имеет меру = 0, т.е.f
~ g,
имеет меру = 0, т.е.f
~ g,

Отношение эквивалентности обладает всеми свойствами: транзитивность, рефлективность, симметричность.
Теоремы об измеримых функциях
1. Если f измерима на Е, то на Е измеримы функции:
1)
 ;
2)
;
2) ;
3)
;
3) ;
4)
;
4) ;
5)
;
5) на Е
на Е
2). Если две функции и измеримы на Е, то на Е измеримы функции:
 ,
,
 ,
,

3). Если функция – непрерывна на измеримом множестве Е, то она измерима на нем.
Свойства измеримости ф-ий:
если μЕ=0 , то f измерима на Е;
f измерима на Е,
 и
измеримо, тоf
измеримо на Е1;
и
измеримо, тоf
измеримо на Е1;если мн-во {Ek} не более, чем счетное сем-во измеримых мн-в и f измерима на Ek для любого k, то f измерима на

если f ~ g измерима на Е и f измерима на Е, то g измерима на Е.
f ~ c (константа) измерима на Е, то f измерима на Е.
Пример
неизмеримой ф-ии:
 ,
если М — неизмеримое подмн-во
,
если М — неизмеримое подмн-во
Последовательности неизмеримых функций:
Последовательность
функций fk
называется
сходящейся к
 почти всюду на Е, если мн-во точек, в
кот. она не сходится имеет меру нуль,
т.е.
почти всюду на Е, если мн-во точек, в
кот. она не сходится имеет меру нуль,
т.е. почти
всюду
почти
всюду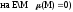 .
.
Теорема:
если fk
измерима
на Е и
 ,
тоf
измерима на Е.
,
тоf
измерима на Е.
Пусть
функции
 и
и измеримы на Е, последовательность
измеримы на Е, последовательность называется сходящейся к
называется сходящейся к по мере, если
по мере, если

Замечание. Существуют последовательности функций, которые сходятся по мере, но не сходятся почти всюду.
Теорема:
Если послед-ть
 сходится к
сходится к по мере, то эта последовательность
сходится к
по мере, то эта последовательность
сходится к почти всюду .
почти всюду .
Теорема
Рисса. Если
последовательность
 сходится к
сходится к по мере на Е, то существует
подпоследовательность
по мере на Е, то существует
подпоследовательность сходится к почти всюду на Е.
сходится к почти всюду на Е.
Теорема
Егорова:
Если послед-ть
 сходится кf
на Е почти всюду, то
сходится кf
на Е почти всюду, то

 мн-во
мн-во и на
и на
 равномерно сходится кf
.
равномерно сходится кf
.
Теорема
Лузина: Если
f
измерима и ограничена на отрезке [a,
b],
то


 —
замкнутое подмн-во отрезка [a,
b],
тогда
—
замкнутое подмн-во отрезка [a,
b],
тогда
 ф-ия φ – непрерывная на [a,
b]
. f
= φ на F
ф-ия φ – непрерывная на [a,
b]
. f
= φ на F
 .
.
