
- •5. Линейное пространство. Евклидово и унитарное пространства
- •6. Линейные операторы и их свойства
- •Линейные преобразования евклидова пространства
- •7. Действительные числа. Функция действительной переменной. Предел функции. Непрерывные функции.
- •8. Производная и дифференциал. Производные и дифференциалы высших порядков. Формула Тейлора
- •9. Основные теоремы дифференциального исчисления и их применения
- •10. Первообразная и неопределенный интеграл
- •4. Интегрирование некоторых тригонометрических функций.
- •6. Интеграл вида если функцияR является нечетной относительно cosx.
- •11. Определенный интеграл Римана, его свойства. Применения к вычислению геометрических, физических и механических величин Определенный интеграл
- •12. Функции нескольких действительных переменных.
- •13. Частные производные и дифференцируемость ф-ции в точке. Производные и дифференциалы высших порядков. Равенство смешанных производных
- •14. Неявная и обратная функции. Экстремумы
- •15. Числовые ряды и их сходимость.
- •16. Функциональные последовательности и ряды. Степенные ряды. Ряд Тейлора.
- •2) Дифференцирование степенных рядов.
- •3) Сложение, вычитание, умножение и деление степенных рядов.
- •18. Ряды Фурье. Преобразование Фурье. Интеграл Фурье
- •Разложение в ряд Фурье четных и нечетных функций
- •Разложение в ряд Фурье функций произвольного периода
- •Представление непериодической функции ряда Фурье
- •Тригонометрический ряд Фурье в комплексной области
- •Свойства ряда Фурье
- •- Неравенство Бесселя.
- •- Равенство Парсеваля,
- •Понятие об интеграле Фурье и об преобразовании Фурье
- •19. Мера Лебега, измеримые множества и функции
- •20. Интеграл Лебега и его свойства.
- •21. Ф-ции комплексной переменной. Диф-ние и инт-ние. Теорема Коши.
- •22. Ряды Тейлора и Лорана. Вычеты
- •Аналитические функции и их разложение в степенные ряды.
- •Свойства максимума модуля аналитических и гармонических функций.
- •Ряд Тейлора.
- •Ряд Лорана.
- •Изолированные особые точки аналитических функций и их классификация.
- •Вычеты и основная теорема о вычетах.
- •Применение к вычислению интегралов.
- •23. Математическое моделирование и вычислительный эксперимент
- •24. Численные методы в алгебре
- •Обусловленность систем линейных алгебраических уравнений
- •Вычисление определителей и обращение матриц
- •Итерационные методы
- •Достаточное условие сходимости итерационного процесса
- •25. Решение нелинейных уравнений и систем уравнений
- •26. Приближение функций.
- •27. Численное дифференцирование. Численное интегрирование
- •28. Решение обыкновенного дифференциального уравнения первого порядка методами Эйлера, Эйлера – Коши, Рунге – Кутты. Метод конечных разностей.
- •29. Разностные методы решения задач математической физики.
- •33. Линейные уравнения и системы.
- •34.Линейные уравнения и системы с постоянными коэффициентами
- •35. Устойчивость решений дифференциальных уравнений
- •Простейшие типы точек покоя. Автономные динамические системы двух уравнений первого порядка. Типы особых точек на фазовой плоскости
- •№37 Физические задачи, приводящие к уравнению параболического типа
- •Интеграл Пуассона
- •39. Алгебра логики
- •3. Основные законы логики.
- •4. Логические функции.
- •5. Нормальные формы. Совершенные нормальные формы.
- •Алгоритм построения сднф.
- •6. Арифметические операции в алгебре логики. Полином Жегалкина.
- •7. Полнота и замкнутость (примеры полных систем). Теорема Поста.
- •Свойства отношений.
- •40. Графы и их свойства
- •41. Маршруты в графах и деревья
- •41. Маршруты в графах и деревья
18. Ряды Фурье. Преобразование Фурье. Интеграл Фурье
Ортонормированная система функций
Опр.
Функции f
и g
из L2
называются ортогональными,
если

Опр.
Функция f
из L2
называется нормированной,
если
 .
.
Опр.
Система функции
 называетсяортонормированной,
если все функции нормированы и попарно
ортогональны: ||ek||
= 1
называетсяортонормированной,
если все функции нормированы и попарно
ортогональны: ||ek||
= 1
 ,
(en,
em)
=
,
(en,
em)
=

Любую
функцию можно нормировать:

 -
множество функций f:
-
множество функций f: ,т.е.L^2
– множество суммируемых квадратов
функций. E-евклидово
пространство.
,т.е.L^2
– множество суммируемых квадратов
функций. E-евклидово
пространство.
Ряд Фурье
Пусть
дано: система {ek}-
ортонормированная
 ,
если
,
если
Находим
 приk
= m.
cm
= (f,
em).
приk
= m.
cm
= (f,
em).
 -
счетная система ортогональных функций,
-
счетная система ортогональных функций,
 .
.
cm = (f, em) – называют коэффициентами Фурье.
 -
ряд Фурье
для функции f
по ортонормированной системе Ek.
-
ряд Фурье
для функции f
по ортонормированной системе Ek. 
Опр. Если ряд (!) сходится и f его сумма, то считается, что f разлагается в ряд Фурье. Частным случаем является:
Тригонометрический ряд Фурье

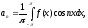


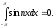



 -
из этих формул вино ортогональность.
-
из этих формул вино ортогональность.


 -
можно заменить.
-
можно заменить.
Все
функции периодические с
 и сумма ряда периодическая.
и сумма ряда периодическая.
Рассмотрим
функцию от
 .
.
Разложение
в тригонометрический ряд Фурье функции
с периодом
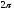
(Теорема Дирихле)
Теорема:
пусть периодическая функция f(x)
c
периодом
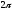 на
на
 удовлетворяет условиям:
удовлетворяет условиям:
f(x) – кусочно-непрерывная (непрерывная или имеет конечное число точек разрыва 1-го рода);
f(x) – кусочно-монотонная (монотонна на всем отрезке или его можно разбить на конечное число частей, на каждой из которых она монотонна).
Тогда соответствующий ряд Фурье сходится и в точках непрерывности его сумма совпадает с f(x).
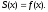
 -
в каждой точке разрыва,
-
в каждой точке разрыва,
на
концах отрезка:
 .
.



 =>
=>





(*) умножим на cosmx:



 =>
=>

 =>
=>




(*) умножим на sinmx:



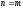



 =>
=>

Замечание:
Если функция удовлетворяет условиям
теоремы на
 ,
то при вычислении коэффициентов, пределы
интегрирования меняются: – π
,
то при вычислении коэффициентов, пределы
интегрирования меняются: – π 0,
π
0,
π 2π.
Все остальное в формулах также.
2π.
Все остальное в формулах также.
Замечание: Теорема Дирихле дает достаточное условие разложимости в ряд Фурье, но не необходимое.
Разложение в ряд Фурье четных и нечетных функций
(сами
функции пока явл. периодич. с
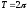 )
)
Пусть f(x) – четная.



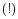
Пусть f(x) – нечетная.


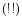




Ряды (!) и (!!) называются неполными рядами Фурье по cos и sin-м соответственно.
Разложение в ряд Фурье функций произвольного периода
Пусть
функция f(x)
– периодическая с периодом T=2l,
будем разлагать в ряд Фурье на [-l,
l].
f(x)
удовлетворяет условиям теоремы Дирихле
на отрезке [-l,
l].
Делаем подстановку:

 должна
быть определена на
должна
быть определена на .
.




проверим,
что она с периодом

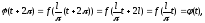 тогда
она определена на
тогда
она определена на
 ,
имеет
,
имеет и удовлетворяет условиям теоремы на
и удовлетворяет условиям теоремы на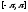 .
.
Разлагаем в ряд Фурье:
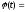





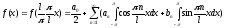





(**) – ряд Фурье для f с периодом 2l.
Если f(x) – четная на отрезке [-l, l], то ряд имеет вид:



Если
f(x)
– нечетная:


Представление непериодической функции ряда Фурье
Пусть
y
= f(x)
– определена на всей числовой оси
 она
не периодическая.
она
не периодическая.
Замечание: Т.к. f(x) - непериодическая, то ее нельзя разложить в ряд Фурье на всей числовой оси, т.к. сумма тригонометрического ряда Фурье является периодической.
Замечание:
Непериодическую функцию можно представить
в виде ряда Фурье на любом конечном
промежутке, на котором она удовлетворяет
условиям Дирихле.

Начало координат помещают в середину [a, b].
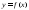


 [-l,
l]
и является периодической с периодом
2l.
[-l,
l]
и является периодической с периодом
2l.Для
 строится тригонометрический ряд Фурье.
строится тригонометрический ряд Фурье.На [a, b] сумма полученного ряда совпадает с функцией f(x) (кроме точек разрыва).
Замечание: Вне отрезка [a, b] сумма ряда и f(x) абсолютно различные функции.
Разложение непериодической функции на отрезке [0, l]:
функция
f(x)
доопределяем на отрезке [-l,
0] и получаем функцию
 ,
раскладываем в ряд на [-l,
l],
тогда верен 4 пункт для отрезка [0, l].
,
раскладываем в ряд на [-l,
l],
тогда верен 4 пункт для отрезка [0, l].
Замечание: Функцию f(x) доопределяют по четности или нечетности, для облегчения разложения в ряд.
