
- •5. Линейное пространство. Евклидово и унитарное пространства
- •6. Линейные операторы и их свойства
- •Линейные преобразования евклидова пространства
- •7. Действительные числа. Функция действительной переменной. Предел функции. Непрерывные функции.
- •8. Производная и дифференциал. Производные и дифференциалы высших порядков. Формула Тейлора
- •9. Основные теоремы дифференциального исчисления и их применения
- •10. Первообразная и неопределенный интеграл
- •4. Интегрирование некоторых тригонометрических функций.
- •6. Интеграл вида если функцияR является нечетной относительно cosx.
- •11. Определенный интеграл Римана, его свойства. Применения к вычислению геометрических, физических и механических величин Определенный интеграл
- •12. Функции нескольких действительных переменных.
- •13. Частные производные и дифференцируемость ф-ции в точке. Производные и дифференциалы высших порядков. Равенство смешанных производных
- •14. Неявная и обратная функции. Экстремумы
- •15. Числовые ряды и их сходимость.
- •16. Функциональные последовательности и ряды. Степенные ряды. Ряд Тейлора.
- •2) Дифференцирование степенных рядов.
- •3) Сложение, вычитание, умножение и деление степенных рядов.
- •18. Ряды Фурье. Преобразование Фурье. Интеграл Фурье
- •Разложение в ряд Фурье четных и нечетных функций
- •Разложение в ряд Фурье функций произвольного периода
- •Представление непериодической функции ряда Фурье
- •Тригонометрический ряд Фурье в комплексной области
- •Свойства ряда Фурье
- •- Неравенство Бесселя.
- •- Равенство Парсеваля,
- •Понятие об интеграле Фурье и об преобразовании Фурье
- •19. Мера Лебега, измеримые множества и функции
- •20. Интеграл Лебега и его свойства.
- •21. Ф-ции комплексной переменной. Диф-ние и инт-ние. Теорема Коши.
- •22. Ряды Тейлора и Лорана. Вычеты
- •Аналитические функции и их разложение в степенные ряды.
- •Свойства максимума модуля аналитических и гармонических функций.
- •Ряд Тейлора.
- •Ряд Лорана.
- •Изолированные особые точки аналитических функций и их классификация.
- •Вычеты и основная теорема о вычетах.
- •Применение к вычислению интегралов.
- •23. Математическое моделирование и вычислительный эксперимент
- •24. Численные методы в алгебре
- •Обусловленность систем линейных алгебраических уравнений
- •Вычисление определителей и обращение матриц
- •Итерационные методы
- •Достаточное условие сходимости итерационного процесса
- •25. Решение нелинейных уравнений и систем уравнений
- •26. Приближение функций.
- •27. Численное дифференцирование. Численное интегрирование
- •28. Решение обыкновенного дифференциального уравнения первого порядка методами Эйлера, Эйлера – Коши, Рунге – Кутты. Метод конечных разностей.
- •29. Разностные методы решения задач математической физики.
- •33. Линейные уравнения и системы.
- •34.Линейные уравнения и системы с постоянными коэффициентами
- •35. Устойчивость решений дифференциальных уравнений
- •Простейшие типы точек покоя. Автономные динамические системы двух уравнений первого порядка. Типы особых точек на фазовой плоскости
- •№37 Физические задачи, приводящие к уравнению параболического типа
- •Интеграл Пуассона
- •39. Алгебра логики
- •3. Основные законы логики.
- •4. Логические функции.
- •5. Нормальные формы. Совершенные нормальные формы.
- •Алгоритм построения сднф.
- •6. Арифметические операции в алгебре логики. Полином Жегалкина.
- •7. Полнота и замкнутость (примеры полных систем). Теорема Поста.
- •Свойства отношений.
- •40. Графы и их свойства
- •41. Маршруты в графах и деревья
- •41. Маршруты в графах и деревья
16. Функциональные последовательности и ряды. Степенные ряды. Ряд Тейлора.
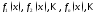 (1)
и все ф-ции опр-ны на мн-ве
(1)
и все ф-ции опр-ны на мн-ве
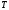 - функц. посл-ть,
- функц. посл-ть,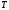 - обл. опр-я ф.п.
- обл. опр-я ф.п.
(1)
сх-ся в т.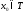 ,
если сх-ся соот. числ. посл-ть (2):
,
если сх-ся соот. числ. посл-ть (2):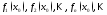 .
Мн-во всех точек из
.
Мн-во всех точек из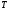 ,
в кот. (1) сх-ся наз. обл. сх-ти ф.п. и обозн.
,
в кот. (1) сх-ся наз. обл. сх-ти ф.п. и обозн.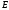 .
.
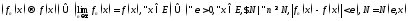 -
(1) сх.
-
(1) сх.
Функциональный ряд - ряд, членами которого являются функции одной действительной переменной.
Ф.р.
сх-ся в т.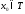 ,
если сх-ся соот. числ. ряд
,
если сх-ся соот. числ. ряд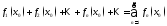 .
.
Если ф. ряд сходится при каждом значении х из множества Е, то множество Е называется обл. сх-ти ряда.
Частич.
суммы ряда:
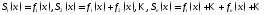 ;
;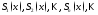 - посл-ть частич. сумм.
- посл-ть частич. сумм.
Ф.р.
сх-ся на мн-ве
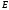 к ф-ции
к ф-ции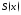 ,
если
,
если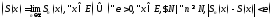 ,
,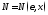 .
.
Ф.р.
наз. абс. сх-ся на мн-ве
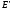 ,
если на этом мн-ве сх-ся ряд
,
если на этом мн-ве сх-ся ряд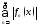 .
.
S(x) = Sn(x) + Rn(x) (2), где Sn(x) = f1(x)+f2(x)+…+fn(x)+… - n-ая частичная сумма, а Rn(x) = fn+1 (x)+fn+2(x)+… -остаточный член ряда (1).
Из равенства (2) видно, что при каждом значении х из области сходимости ряда имеем: lim Rn(x)=0 (n→∞) и, следовательно, для любого ε>0 существует такой номер N, что для всех n>N в этой точке х будет верно неравенство: ׀Rn(x)׀<ε.
Если для любого ε>0 существует такой номер N, не зависящий от х,что для всех n>N в этой точке х верно неравенство: ׀Rn(x)׀<ε для всех х из множества Е, то данный функциональный ряд называется равномерно сходящимся на множестве Е.
Кр.
Коши равномер. сх-ти ф.р.:
для равномер. сх-ти ф.р. на мн-ве
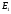 н. и д., ч.
н. и д., ч.
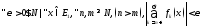 .
.
Док-во:
Равномер.
сх-ть ф.р. означ. равномер. сх-ть ф.п. его
частич. сумм, т.е. это означ. равномер.
сх-ть фундам. посл-ти частич. сумм:
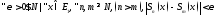 .
.
Теорема
Вейерштрасса: Если
для ф.р.
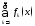 (3)
(3) сх-ся числ. положит. ряд
сх-ся числ. положит. ряд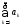 (7) такой, что на мн-ве
(7) такой, что на мн-ве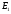
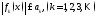 (8), то (3) сх-ся абсолютно и равномерно
на
(8), то (3) сх-ся абсолютно и равномерно
на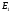 .
.
Док-во:
(8) =>
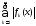 сх-ся по пр. сх-ти положит. рядов, тогда
ряд (3) сходится, притом абсолютно.
сх-ся по пр. сх-ти положит. рядов, тогда
ряд (3) сходится, притом абсолютно.(7) сх-ся по кр. Коши для ч. ряда.
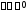
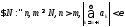
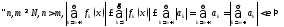
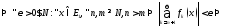 (3)
сх-ся равн-но на
(3)
сх-ся равн-но на
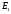 .
чтд
.
чтд
Т.:
если
ф-и
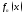 опр. на мн-ве
опр. на мн-ве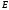 ,
непр. в т.
,
непр. в т.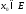 и равномер. сх-ся к ф-ции
и равномер. сх-ся к ф-ции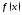 на
на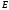 ,
то и ф-я
,
то и ф-я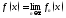 непр. в т.
непр. в т.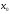 .
.
Док-во:
если
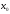 - изолир. т., то
- изолир. т., то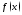 непр. в т.
непр. в т.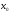 по опр-ю.
по опр-ю.
если
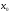 -предел. т., то нужно док-ть, что
-предел. т., то нужно док-ть, что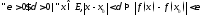 .
.
Равн.
сх-ть:
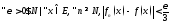
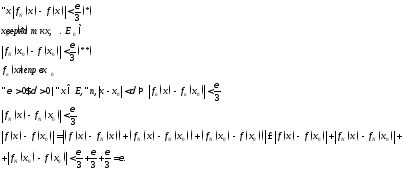
Т.:
если
ф-и
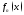 опр. на мн-ве
опр. на мн-ве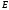 ,
непр. в т.
,
непр. в т.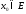 и ряд
и ряд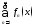 сх-ся на
сх-ся на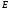 равномерно, то сумма ряда есть непр.
ф-я в т.
равномерно, то сумма ряда есть непр.
ф-я в т.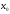 .
.
Т.:
если
члены ф.р. непр. на
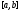 ,
а сам ряд на отрезке
,
а сам ряд на отрезке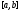 сх-ся равн-но, то возможно почленное
интегрирование ряда.
сх-ся равн-но, то возможно почленное
интегрирование ряда.
Т.:
Пусть
выполнены условия: 1)
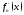 непр. на
непр. на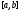 ;
2) ряд
;
2) ряд
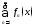 сх-ся и имеет своей суммой
сх-ся и имеет своей суммой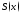 ;
3) ряд, сост. из произ-х сх-ся на
;
3) ряд, сост. из произ-х сх-ся на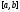 равномерно. Тогда сумма ряда диф-ма на
равномерно. Тогда сумма ряда диф-ма на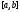 и возможно почленное диф-ние ряда.
и возможно почленное диф-ние ряда.
Док-во:
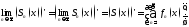
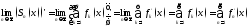
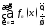 =
=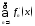 .
.
Функциональный ряд вида: а0 + а1х + а2х2 + … + аnхn + … (1), где а0, а1 , а2 , … аn - постоянные коэффициенты, называется степенным рядом.
Для исследования на сходимость степенных рядов удобно использовать признак Даламбера.
Применяем
признак Даламбера:
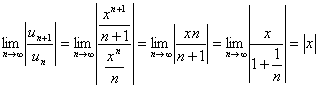 .
.
Теоремы
Абеля.
Если
степенной ряд
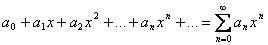 сходится
приx
= x1
, то он сходится и притом абсолютно для
всех
сходится
приx
= x1
, то он сходится и притом абсолютно для
всех
![]() .
.
Следствие.
Если при х
= х1
ряд расходится, то он расходится для
всех
![]() .
.
Таким
образом, для каждого степенного ряда
существует такое положительное число
R,
что при всех х
таких, что
![]() ряд
абсолютно сходится, а при всех
ряд
абсолютно сходится, а при всех![]() ряд
расходится. При этом числоR
называется радиусом
сходимости.
Интервал (-R,
R)
называется интервалом
сходимости.
ряд
расходится. При этом числоR
называется радиусом
сходимости.
Интервал (-R,
R)
называется интервалом
сходимости.
Отметим, что этот интервал может быть как замкнутым с одной или двух сторон, так и не замкнутым.
Радиус сходимости может быть найден по формуле:
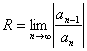
Ряд Тейлора. Пусть функция f(x) определена и имеет производные любого порядка на некотором отрезке. Пусть точки а и х принадлежат этому отрезку. Выразим данную функцию по формуле Тейлора:
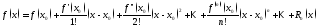 .
(
.
(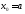 )
)
Если окажется, что Rn(x) →0 при n→∞, то получим: f(x) = lim (n→∞) {f(a) + [f'(a)/1!](x-a) + … + [f(n-1)(a)/(n-1)!](x-a)n-1}, а это означает, что f(x) представляет сумму ряда, у которого n-ая частичная сумма есть выражение, содержащееся в фигурных скобках, т.е. f(x) = f(a) + [f'(a)/1!](x-a) + … + [f(n)(a)/(n)!](x-a)n +… (1).
При а=0 равенство (1) принимает вид: . f(x) = f(0) + [f'(0)/1!]x + … + [f(n)(0)/(n)!]xn +… (1') и представляет разложение функции f(x) в степенной ряд по степеням х.
Теорема.
Если степенной ряд
![]() сходится
для положительного значениях=х1
, то он сходится равномерно в любом
промежутке внутри
сходится
для положительного значениях=х1
, то он сходится равномерно в любом
промежутке внутри
![]() .
.
Действия со степенными рядами.
1)
Интегрирование степенных рядов.
![]() ,
,![]()
