5. Линейное пространство. Евклидово и унитарное пространства

Множество называетсявекторным (линейным) пространством над полем , если

1. имеется правило, посредством которого для ставится в соответствие третий элемент, называемый суммой элементови;

2. имеется правило, посредством которого и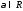ставится в соответствие элементили, называемый произведением элементана число;

3. указанные два правила подчинены следующим восьми аксиомам:

1. (переместительное свойство суммы);

2. (сочетательное свойство суммы);

3. такой, что (особая роль нулевого элемента);

4. такой, что (особая роль противоположного элемента);

5. (особая роль числового множителя 1);

6. (сочетательное относительно числового множителя свойство);

7. (распределительное относительно суммы числовых множителей свойство);

8. (распределительное относительно суммы элементов свойство).

Элементы векторного пространства называются векторами, а числа из (можно рассматривать и поле) –скалярами.

Скалярным произведением называется отображение :, где имеют место аксиомы, при:

1) - симметрия,

2) - аддитивность,

3) - однородность,

4) a ≠0 

Векторное пространство с введённым на нём скалярным произведением называется евклидовым (унитарным) пространством.

Линейная зависимость векторов.

Упорядоченная система чисел называется -мерным вектором.

(-ая декартова степень поля)

. Алгебраическая операция:

Опр.:

Опр.: Система (совокупность) векторов 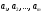(1) - линейно зависимая, если найдутся(2) не все равные нулю(хотя бы одно не равно нулю), что(3)- линейная комбинация системы (1) с коэффициентами из системы (2) равна нулевому вектору.

Опр.: Система (1) называется линейно независимой, если линейная комбинация (3) равна - лишь в единственном случае, когда

Св-ва:

1)Всякая система (1), содержащая нулевой вектор, является линейно зависимой. (1),

2)Всякая система, содержащая коллинеарные (параллельные) векторы, является линейно зависимой.

3)некоторая подсистема системы (1) линейно зависимая (1), тогда и вся система л. з.(1) л. з.

Основная теорема о линейной зависимости.

Пусть даны a₁,a₂,…, a_r(1); b₁, b₂,…,b_s(2), (1) – л.н.з. и каждый вектор (1) системы линейно выражается через (2), r≤s. a_j = |j=1,2…r., (3), тогда система (1) - л. з. система.

Д-во. Коэф-ты лин. выражений (3) составляют систему из r s-мерных векторов: . Т.к.r>s, то эти век-ры лин. зав-мы,т.е. , где не все коэф-тыk₁,k₂,…,k_r равны 0. Отсюда: (4). Рассм. след. лин. комб-ю век-ров сист. (1):или. Используя (3) и (4), получаем:, а это противоречит лин. незав-ти сист. (1). ч.т.д.

Конечномер. лин. пр-ва, базис, размерность. Лин. подпр-ва, лин. оболоч.

Лин. пр-во V наз. конечномерным, если в нем можно найти конечную максимальную линейно независимую систему векторов (м.л.н.з. система - если добавление к ней любого вектора даёт уже л.н.з. систему). Всякая такая система – база пр-ва V(две базы состоят из одинакового количества векторов). Пусть дано конечномерное пространство , возьмём в нёмa₁,a₂,…,a_s(1) векторов. Кол-во векторов, входящих в базу этого пр-ва, наз-сяразмерностью этого пр-ва. Рассмотрим всевозм. лин. комб. сист(1): {α₁a₁ + α₂a₂ + … + α_Sa_s | α_i полю P}(2) V. ] a = α₁a_{1 +…+} α_sa_s , b = β₁a_{1 +…+} β_sa_S => a+b = (α₁+β₁)a₁ + … + (α_s+β_S)a_s и γa = (γα₁)a_{1 +…+} (γα_s)a_s(2) => (2) – подпр-во, порожд. сист. (1), <(a₁,a₂,…,a_s), + , α> - лин. оболочка (1) (т.е. пространство векторов, натянутых на систему): , где,-поле комплексных чисел.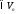

Подмн-во L лин. пр-ва V наз-ся лин. подпростр-вом этого пр-ва, если оно само явл-ся лин. пр-вом по отн-ю к определённым в V операциям сложения векторов и умножения вектора на число. Для того, чтобы непустое L было лин. подпр-вом V, достаточно: 1) если векторы a и b принадл. L, то a+b – тоже принадл. L; 2) если a принадл. L, то αa – принадл. L при любом α.

Преобразование координат вектора при изменении базиса.

Две системы векторов пространства ,являются базами данного пространства, когда сущ-ют две невырожденные матрицыи, что.Различных баз в -мерном пр-ве над полем сущ-ет столько, сколько сущ-ет различных невырожденных матриц -го порядка из.

Линейные многообразия.

Подпр-во ,- линейное многообразие пр-ваV_n, получ. сдвигом пр-ва на вектор.

Т-ма: Многообразие можно получить сдвигом лишь единственного векторного пр-ва: .

Д-во. ] M = {a+V_m}={a′+V_m′}. .. a+y = a′+y′...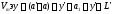

Т-ма: Всякое лин. многообр. можно задать сист. лин-х неодн. уравнений.

Ортонормированный базис. Процесс ортогонализации.

Опр.: Два вектора называютсяортогональными (перпендикулярны), если -скалярное произведение. Система векторов ортогональная, если

Т-ма: Любая сист. попарно ортогональных векторов пр-ва л.н.з.

Замеч.: Если в имеемштук ортог. л.н.з. векторов, значит это база.

Т-ма (Метод Шмидта): Каждую л.н.з. систему векторов можно преобразовать в ортогональную систему векторов(в частности каждую базу можно преобразовать в ортог. базу).

Опр.: Вектор называется нормированным, если -скаляр. квадрат=1

Зам.: Любой ненулевой вектор можно нормировать.

Т-ма: База евклид. пр-ва явл-ся ортонормированной , когда скаляр. произведение двух любых векторов взятых в данной базе = сумме произведения одноимённых координат.- ортонор. база

Ортогональное дополнение.

-подпространство,

Ортогональное дополнение к подпространству: - всевозможные векторы Евклид. пр-ва ортогон. ко всем векторам всех подпространств.

Геометрические св-ва мн-ва решений сист. лин-х алг-х ур-й с т. зрения факторов лин. пр-ва.

Мн-во решений сист. лин-х однор. ур-й – векторное пр-во.

Мн-во решений сист. лин-х неоднор. ур-й – многообразие.