§9. Газ во внешнем поле, распределение Больцмана.

Возьмем цилиндрический сосуд и взвешивая его наполненный газом и откачанный, мы получим разность веса равную весу газа. Но эта разность может появиться только если концентрация молекул у верхнего торца и нижнего в поле тяжести разная, причем большая концентрация должна быть у нижнего торца. Действительно учитывая, что P = nkT, при постоянной температуре газа по высоте суммарный вес молекул

mg = (Р0 – Рh)*S = (n0 – nh) kTS не равен нулю, только если концентрация молекул

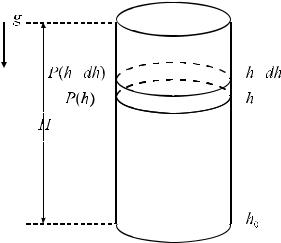
унижнего торца выше. Отсюда следует, что в силовом поле происходит перераспределение концентрации молекул. Попробуем найти это распределение. Возьмем в сосуде наполненном молекулами массой m, имеющим постоянную по высоте температуру Т, тонкий слой толщиной dh на некоторой высоте h, примем что в этом слое концентрация n(h) (рис 7) тогда разность силы давления будет:

(Р(h+dh) – P(h))S = -dP*S = mgn(h)dhS отсюда:

dPdh mgn(h) учтя, что P = nkT получим kT dndh mgn(h) разделяя переменные получим: dnn mgdh интегрируя имеем ln(n) = - mghkT C . Константу С найдем полагая, что

Рис. 7. К выводу зависимости концентрации молекул от высоты n(h) в поле тяжести

Такая зависимость давления от высоты в поле тяжести Земли носит название барометрической формулы. Если нам известны n0 или Р0 задача по нахождению концентрации и давления на разных высотах решена. Чему будут равны эти величины, если в поле тяжести, в цилиндрический сосуд высотой H, площадью основания S, поместили N частиц, массой m при температуре T ? Найдем n0 . Предположим, что n0 нам известна, тогда интегрируя по всему объёму сосуда мы получим N

22

распределения по абсолютной величине скорости скорости будет m 3 mv2

dW(v) =4 ( 2 kT )2 e- 2kT v2 dv

заметим, что при выводе этих распределений мы не использовали вида взаимодействия молекул и эти распределения справедливы как в модели твердых шариков, так и в модели взаимодействующих молекул.

Похожие распределения мы получили в случае нахождения распределения концентрации частиц в силовом поле:

получим вероятность обнаружения частицы в заданной части пространства, с заданной

Максвелла-Больцмана.

Во всех этих распределениях присутствует экспонента, в показатели которой энергия частицы деленная на kT. В случае распределения Максвелла это кинетическая энергия, в распределениях Больцмана потенциальная. Собственно основная заслуга Больцмана заключается в том, что он понял, в распределении частиц обязательно будет присутствовать экспонента, в показатели которой энергия частицы деленная на kT. Не вдаваясь в подробности, укажем, что это присутствует даже в квантовых статистиках, когда энергия может принимать дискретный ряд значений - уровней. Для средней заселённости

ekT 1

Заметим также, что пока kT меньше разности энергий между основным и первым возбужденным состоянием подавляющее число молекул находится в основном состоянии. Говорят, что эти степени свободы выморожены. Поэтому колебательные и вращательные степени свободы начинают проявляться при достаточно высокой температуре. Эти температуры естественно будут разными для различных молекул, а также будут зависеть от агрегатного состояния вещества – газ, твердое тело. Для поступательных степеней свободы молекул в газообразном состоянии эти эффекты проявляются при температурах близких к абсолютному нулю, поэтому для них справедлив классический подход выражающейся распределением Максвелла.

24

§11. Закон равнораспределения

Как мы уже получили, средняя энергия поступательного движения = К =3kT2 , учитывая независимость распределения по скоростям по различным осям

средняя энергия не зависит от массы молекулы, т.е. молекулы в смеси газов будут иметь

одинаковы и равны 3kT2 . Но если молекула состоит из нескольких атомов, появляется

энергия связанная с её вращением и колебаниями атомов относительно равновесного положения. С этими движениями также будет связана соответствующая энергия. Разберем ситуацию для случая двухатомной молекулы. Направим ось z вдоль линии соединяющей молекулы. Тогда момент инерции Iz =0. а энергия связанная с вращениями по осям x и y

потенциальной энергии связанной с смещением молекул x относительно положения

эти два члена в энергии колебаний и аналогию с разобранными выше ситуациями получим, что на каждую колебательную степень свободы приходится по

kT2 + kT2 =kT

Квантовая природа молекулярных движений вносит коррективы в эту простую картину. Энергия может изменяться дискретными порциями – квантами. Поэтому когда температура мала – меньше первого уровня изменения энергии, соответствующая степень свободы не возбуждена и не вносит вклад в энергию хаотического движения. Поступательные степени свободы появляются при очень низких температурах, затем при

повышении температуры, когда kT Евр начинают возбуждаться вращательные степени

25