FIT_Fizika_2-3

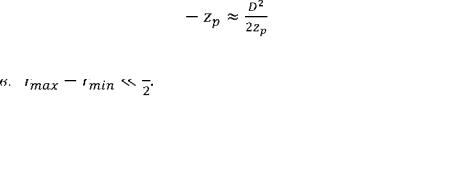
Окончательно с учетом сделанных приближений находим разность фаз k(Rt - Д0) = ~к(г± • еР) = -к (хг f; + У1J),

что совпадает с подынтегральным выражением интеграла Кирхгофа в приближении Фраунгофера, Важно, что приняв приближенное выражение для R±, мы приняли, что вектора R0 и Rx являются параллельными - именно в этом случае оно справедливо, Это и выполняется в приближении Фраунгофера, когда точка наблюдения отстоит от отверстия очень далеко, Следовательно, волны, порожденные различными участками волнового фронта, идут параллельно друг другу, поэтому дифракцию Фраунгофера называют также дифракцией в параллельных лучах, Разность фаз этих волн такая же, как и у плоских волн, порождаемых находящимися на некотором расстоянии друг от друга синфазными источниками, Как вывод из всего вышеизложенного, дифракция Фраунгофера определяется интерференцией плоских волн, синхронно излучаемых поверхностью волнового фронта в заданном направлении, Отсюда следует вывод об устойчивом угловом распределении поля при данной дифракции,

Осталось разобраться, при каких расстояниях выполняются полученные приближения, и связать их с рассмотренной ранее величиной разности фаз волн в точке наблюдения от разных участков волнового фронта, Давайте дадим определение: зона Френеля - область поверхности волнового фронта, фазы волн в точке наблюдения от различных участков которой различаются не более чем на п, Для этого разность расстояний от различных точек зоны Френеля до точки наблюдения не должна превышать Я/2, Из рассмотренного ранее следует, что волны от одной зоны Френеля, складываясь, усиливают друг друга,

Пусть характерный размер отверстия в экране равен D, Тогда разность максимального и минимального расстояний от разных точек экрана до точки наблюдения будет порядка

Эта разность зависит от расстояния zp, Рассмотрим три случая

Отношение —-D2обычно называют параметром Френеля, Этот параметр ха-

рактеризует число открытых зон Френеля в экране с характерным размером отверстия D для наблюдателя, находящегося на расстоянии zp от экрана,

Для случая а расстояние от экрана до плоскости наблюдения zp должно

быть

61

D2

Zp <<—.

Это случай геометрической оптики. Открыто очень много зон Френеля, итоговая амплитуда поля в каждой точке плоскости наблюдения постоянна - не меняется при изменении размеров отверстия в экране или изменении расстояния Zp, пока выполняется соответствующее условие. Эта амплитуда равна амплитуде поля перед экраном (или равна нулю, если точка наблюдения лежит в области геометрической тени). Таким образом, в этом случае дифракционная картина не изменяется при изменении zp.

Для случая в расстояние zp должно быть

D2

zp »—

афазы различных волн практически совпадают. Это есть условие дифракции Фраунгофера. Отверстие в экране составляет только малую часть зоны Френеля; говорят, что отверстием в экране открыта только часть первой зоны Френеля. Дифракционная картина изменяется подобно самой себе в зависимости от Zp. Интенсивность поля в подобных точках дифракционной картины монотонно спадает по мере удаления точки наблюдения от экрана и монотонно возрастает при увеличении размера отверстия.

Случай б является промежуточным. При этом

D2 Z P я,

открыто несколько зон Френеля, дифракцию необходимо рассматривать в приближении Френеля. Интенсивность поля в точке наблюдения периодически меняется от минимальной до максимальной при изменении положения этой точки или изменении размеров отверстия (если при этом последовательно открываются и закрываются зоны Френеля). Таким образом, дифракционная картина существенным образом зависит от zp.

Дифракция Френеля на щели

Рассмотрим падение плоской монохроматической волны на длинную прямоугольную

конечности. Если разделить подынтегральную функцию в интеграле Кирхгофа по переменным х и у, то по х можно сразу проинтегрировать:

62

Введем переменную

Д;(у-ур1

“RZp

Здесь введены так называемые интегралы Френеля:

C(v) = Jcos(^fj da, S(V) = fsin(^

da.

Рисунок 42. Спираль Корню.

Комплексная функция вещественного переменного z(v) = C(v) + iS(v) описывает в параметрическом виде на комплексной плоскости кривую, изображенную на рисунке 42 и называемую спиралью Корню. Итоговую амплитуду колебаний опять можем найти в виде модуля вектора на комплексной плоскости, соединяющего две точки z(v1) и z(u2) на этой спирали.

Найдем распределение интенсивности тени от края полубесконечного экрана. Совместим начало системы координат с краем экрана, в этом случае

Vi = v1(yP) = - f ^ y p , v2 = от, C(v2) = S(v2) = j.

^ = 54(5-+ КИМ

0-cC^)) +(^-S(Ul))

63

График распределения интенсивности на плоскости наблюдения, нормированной на интенсивность /0 вдали от края экрана, представлен на рисунке 43. Осталось отметить, что величина ^A.zP, которая задает масштаб дифракционной картины, определяет ширину зон Френеля.

Рисунок 43. Распределение интенсивности при дифракции на крае полубесконечного экрана.

На примере дифракции на щели конечных размеров можно нагляднее всего показать переход от дифракции Френеля к дифракции Фраунгофера. Распределение интенсивности на плоскости наблюдения для разных значений параметра Френеля схематически изображено на рисунке 44. Видно, что при дифракции Френеля распределение интенсивности существенно меняется при изменении этого параметра, но сам размер освещенной области в целом не изменяется. При дифракции Фраунгофера не изменяется форма распределения интенсивности, но размер освещенной области увеличивается - световой пучок из-за дифракции расходится.

Рисунок 44. Переход от дифракции Френеля к дифракции Фраунгофера.

64

Дифракция Фраунгофера на прямоугольном отверстии

Рассмотрим, как преобразуется ранее полученный результат с ростом расстояния от экрана. В этом случае воспользуемся интегралом Кирхгофа в приближении Фраунгофера:

E 0 D x D y s in (a x ) sin(a y )

где введены обозначения

n = kxp_Dx n = k y p D y

W- V « vt-ЛТ .

* zP 2 У Zp 2

Следовательно, интенсивность можно представить в виде

^рл = j sin 2 (a x ) s in 2 (a y )

( Хх ССу

1 0 - интенсивность в центре дифракционной картины.

Рисунок 45. Распределение интенсивности при дифракции на прямоугольном отверстии.

Распределение интенсивности на плоскости наблюдения при изменении одной из ее координат и при фиксированном значении другой координаты показано на рисунке 45. Видно, что подавляющая доля световой энергии сосредоточена в центральной области, ограниченной по а от - п до п. Можно тогда сказать, что на большом расстоянии от щели

Это соотношение верно не только щели, но и приближенно выполняется для любых форм отверстий в экране.

65

2.5Дисперсия света

Мы с вами изучали, что скорость распространения электромагнитных колебаний в

среде

_ с — с п

Как же с физической точки зрения происходит взаимодействия света и среды? Электромагнитные волны воздействуют на заряженные частицы среды, заставляя их совершать вынужденные колебания на частоте поля. При этом, как и при всяком вынужденном колебании, часть энергии поля передается частицам, т.е. энергия световой волны поглощается. Колеблющиеся частицы, в свою очередь, становятся источниками вторичных световых волн. Интерференция этих волн и приводит к тому, что скорость распространения света в среде меньше, чем в вакууме. Боле того, эта скорость становится зависимой от частоты световой волны. Это явление называется дисперсией света. Наиболее известное проявление дисперсии - разложение белого света в спектр при прохождении через призму.

Разберем это явление подробнее. В обычных условиях число атомов вещества столь велико и они расположены столь близко друг к другу, что дискретная структурасреды никак среда. Это ипозволило всвое время ввести вектора поляризации Ри намагни чения М вещества, диэлектрическую и магнитную проницаемости £ и д:

Р= /еЕ, М = *тН,

D= £Е, В = дН,

£= 1+ 4пХе, Д =1 + 4пХт.

Здесь Хе и Хт - диэлектрическая и магнитная восприимчивости. Такая связь напряженности внешних полей (Е и Н) и отклика среды (Р и М) сводится к простой пропорциональности. С физической точки зрения это означает безинерционность, локальность, линейность и изотропию среды. Безинерционность и локальность означают, что величина векторов Р и М в некоторый момент времени и в некоторой точке пространства полностью определяются значениями внешних полей в это же точке и в этой же точке. Линейность и изотропия - что уравнения линейны, а величины Хе и Хт являются скалярными, а не векторными величинами.

Среды с локальной и безинерционной зависимостью Р(Е) называют недис-

пергирующими, нелокальность приводит к пространственной дисперсии, а

инерционность, т.е. запаздывание Р относительно Е - к временной, или частотной дисперсии. Независимо от дисперсии, среды могут быть линейными или нелинейными, изотропными или анизотропными.

Давайте далее рассматривать диэлектрические, нейтральные и немагнитные среды. К ним относятся газы, стекла, жидкости, пластмассы и т.п., то есть

66

все наиболее важные для оптики среды. Уравнения Максвелла имеют вид совпадают с записанными далее, материальное уравнение среды в общем виде

D = D(E).

В силу определения

D = Е + 4TTP,

эта зависимость может быть представлена в виде, который и будем понимать далее под материальным уравнением:

Р = Р(Е).

Тогда волновое уравнение в диспергирующей среде принимает вид

Для линейных изотропных сред это уравнение переходит в

Это уравнение в математическом виде показывает, что поляризация среды является источником светового поля.

Электронная теория дисперсии Лоренца

Отыскание явного вида зависимости Р = Р(Е) сводится к решению уравнения, описывающего движение зарядов. Для этого рассмотрим атом как осцилляторнуюсистему 2000 раз большей, чем электроны, его можно считать неподвижным при нало жении внешнего переменного поля, будем рассматривать движение только электронов.

Пусть в отсутствие внешнего поля молекулы или атомы среды нейтральны, появление же поля смещает электроны на расстояние г, образуя в среде дипольный момент

Р = Ne г,

где N - число атомов в единице объема вещества. Это смещение, конечно же, определяется полем Е:

г = Г(Е).

Для нахождения этой зависимости воспользуемся уравнением движения Ньютона

d 2 r v

т7^ = ЪЪ.

Примем, что кроме внешней силы, на электрон действую еще две силы:

1. Сила, удерживающая его в положении равновесия. Примем, что это квазиупругая сила

F = —кг;

67

2.Сила, вызывающая затухание колебаний. Примем, что эта сила описывается аналогично силе трения F = —77г.

Внешняя сила есть сила со стороны электрического поля F = —еЕ, следовательно, уравнение движения приобретает вид

г + уг + ^>пГ = —Е.

ной частоты осциллятора, в данном случае электрона в атоме. Будем рассматривать периодическую вынуждающую силу Е(0~е“^. Частное решение урав-

Следовательно, линейная восприимчивость среды и диэлектрическая проницаемость будут иметь вид

Диэлектрическая проницаемость получилась комплексной, следовательно, показатель преломления среды и волновое число тоже будут комплексными величинами. Обозначим их действительную и мнимую части следующим образом:

п = п' — in", к = к' — ik" = —{п' — in").

с

Пусть плоская монохроматическая волна распространяется в среде вдоль оси z. Тогда поле волны можно представить в виде

Е = E0exp{i{^t — kz)) = E0exp(—k"z)exp(i(<x>t — k'z)).

Следовательно, мнимая часть волнового вектора определяет затухание волны в среде, а действительная - скорость ее распространения. Поскольку к' = к'(ш), скорость перемещения точки волны с постоянной фазой также зависит от частоты - пришли к явлению дисперсии. Интенсивность света зависит от z как

/(z) = /0е-йг,

где b = 2к" = 2—п". Эта зависимость известна как закон Бугера, она определяет поглощение света при его распространении в среде. Показатель преломления и коэффициент поглощения выражаются комплексную диэлектрическую

проницаемость среды следующим образом:

" ” СО

с

п'{ш) = Re Л/£(^) , Ь(ш) = 2 2^ 1т ^Е(Ш)

Если ввести плазменную частоту как

68

то диэлектрическая проницаемость запишется в виде

Ј(to) = 1 +

Анализ этого выражения проведем, разделив среды на разреженные и плотные.

Разреженные среды

В разреженных средах плотность атомов в веществе N мала. Это позволяет, воспользовавшись известной формулой математического анализа

(1 + х)а «1 + ах при х « 1,

представить показатель преломления и коэффициент поглощения диспергирующей среды в виде

Рисунок 46. Зависимость показателя преломления и коэффициента поглощения от частоты.

Графики зависимости этих величин от частоты представлены на рисунке 46. В этих графиках наблюдается знакомая картина резонанса - вблизи собственной частоты системы значительно увеличивается поглощение волны средой. Разобьем весь диапазон частот на три части. В областях I и III, вдали от собственной частоты, коэффициент поглощения мал, показателя преломления слабо отличается от единицы, а его величина увеличивается с ростом частоты: — > 0 - это

условие определяет область нормальной дисперсии. В области II ^ <0 - это

69

область аномальной дисперсии. Величина коэффициента поглощения в этой области уже значительна, поэтому соответствующий ей диапазон частот также называется полосой поглощения.

Если атомы и молекулы вещества имеют несколько резонансных частот, то будет несколько полос поглощения, в каждой из которых будет наблюдаться аномальная дисперсия.

Плотные среды

При рассмотрении дисперсии в разреженных средах мы полагали, что на атом воздействует только поле световой волны. Если же среда достаточно плотная, то расстояния между атомами невелики, и необходимо учитывать их взаимное влияние. В электростатике было введено эффективное поле в среде при наличии внешнего поля Е:

4п

Еэфф = Е +

Тогда уравнение движения можно записать для вектора Р:

Р + УР + ^Р^+ТР).

Для области прозрачности, когда |^ — &>0| >> у, это уравнение приводит к следующему уравнению для показателя преломления среды

П2 — 1 1 Шр

п + 1 3 WQ-W '

Данное выражение называют формулой Лоренца-Лоренца в честь датского физика Людвига Лоренца и голландского физика Хендрика Лоренца, получивших ее независимо друг от друга.

2.6Фазовая и групповая скорости

Говоря о плоской монохроматической волне, мы записывали ее зависимость от координаты и времени как

f(z,t) = f0cos(kx — k>t).

Найдем скорость перемещения точки волны с определенной фазой (это может быть один из максимумов или минимумов волны). Эта скорость определяется из условия

кх — wt = const, к dx — ш dt = 0, — = — = уф. ’ dt к ф

Для сред с дисперсией мы видели, что в эту формулу должна входить реальная часть волнового числа, и получали зависимость волнового числа от частоты в виде

k'{^)=—Re VЈ(^)

70