FIT_Fizika_2-3

ла меньше заданной, и выключать, если больше - не подходит, поскольку вследствие инерционности нагревателя колебания температуры тела будут слишком большими. Давайте поступим иначе - будем включать и выключать нагреватель достаточно часто, настолько, чтобы тело не успело сколько-нибудь изменить свою температуру за этот цикл. Мощность нагрева, поступающая от нагревателя телу, будет определяться тогда соотношением времен включения и выключения, и если эту величину регулировать при помощи обратной связи, то можно добиться высокой стабильности температуры. Такая модель управления называется широтно-импульсной модуляцией и, естественно, применяется не только для стабилизации температуры, но и во многих областях техники.

Рисунок 20. Схема ШИМ.

Рисунок 21. Периодический сигнал, формируемый источником.

Рассмотрим источник прямоугольного периодического сигнала, подключенный к фильтру низких частот, как показано на рис 20. Сигнал имеет период Т, время включения т и амплитуду Е0 (см. рис. 21). Что будет на выходе фильтра, если его частота среза много меньше частоты сигнала? Разложим входной сигнал в ряд Фурье:

А0

оо

E(t) = — + у ^ [Ancos{nu>t) + Bnsin(n^t)],

п=1

где to = 2л/Т - частота основной гармоники. ФНЧ ослабляет периодический сигнал, что математически выражается в уменьшении амплитуд гармоник, причем чем больше номер п гармоники, тем сильнее уменьшается ее амплитуда. В рассмотренном случае фильтр очень сильно ослабляет амплитуды всех гармоник, соответственно, их можно рассматривать как малые колебания около постоянного уровня, определяемого постоянным коэффициентом в разложении Фурье, который не изменяется фильтром. Вспоминая формулу для его отыскания, сразу определяем этот уровень:

21

Оказывается, что изменением скважности сигнала (отношением т/71) можно линейно изменять уровень постоянного выходного сигнала. Эта схема применяется очень часто, поскольку, во-первых, ее можно просто и компактно реализовать на практике; во-вторых, в отличие от прочих схем ее КПД очень велик - ключи, формирующие периодический сигнал, практически не потребляют мощности. Например, на ее основе устроены все блоки питания компьютеров.

1.7Применение закона электромагнитной ин дукции

Закон электромагнитной индукции, открытый английским физиком Майклом Фарадеем, гласит, что для любого замкнутого контура индуцированная электродвижущая сила равна скорости изменения магнитного потока Ф, проходящего через этот контур:

Этот закон лежит в основе электротехники, которая, как не будет преуменьшением сказать, является ядром современной цивилизации. Причина этому в том, что электрическая энергия является наиболее удобной из форм энергии, доступных человеку, во многом благодаря закону электромагнитной индукции. Действительно, и получение электрической энергии (электрогенераторы), и ее трансформация, и ее преобразование в механическую энергию (электродвигатели) - все это осуществляется согласно закону Фарадея, причем с высоким КПД.

Первнчная обмотка Вторичная обмотка

Рисунок 22. Схема трансформатора.

Давайте оставим за рамками работу электродвигателей и генераторов, и рассмотрим работу трансформатора. Обычно он состоит из двух обмоток на общем железном сердечнике, как показано на рисунке 22. Железный сердечник необходим для того, чтобы поток магнитного поля, создаваемый первичной обмоткой, направить сквозь вторичную обмотку. В этом случае коэффициент взаимной индукции обмоток максимален и равен

м = ЩТ2,

22

где L± и L2 - коэффициенты самоиндукции обмоток.

Рисунок 23. Эквивалентная схема трансформатора.

Непосредственно расчет трансформатора будем проводить на основе его эквивалентной схемы, представленной на рисунке 23. Запишем для цепей каждой из обмоток 2-е правило Кирхгофа:

Отсюда из второго уравнения выражаем ток в первой обмотке через ток во второй

и подставим его в первое уравнение:

Ё = [1шМ -^(ZH + i(0L2)\ I2 = ~[L1ZH + i0){L1L2 - M2)]|. Напряжение на

нагрузке

fj 7 7 _________ E MZU ______

н _ 2 н _ L1ZH + iu(L1L2-M2).

Видно, что при M < ■^L1L2 уменьшается коэффициент трансформации. Обычно рассеяние магнитного потока в трансформаторе очень мало, соотношение выполняется с хорошей точностью, и коэффициент трансформации равен

Uh N,

Ел1 L± N±

где N2/Nt - отношение числа витков обмоток.

1.8Длинные линии

Рассмотрим коаксиальный кабель, пространство между внешней оплеткой и центральным проводником (жилой) которого заполнено диэлектриком с диэлектрической проницаемостью £ и магнитной проницаемостью ^ « 1. Из курса электростатики известно, что такая конструкция представляет собой конденсатор, причем чем длиннее кабель, тем больше его емкость. При рассмотрении таких конденсаторов вводят удельную емкость (емкость на единицу длины). Из курса же магнитостатики известно, что у такого кабеля есть индуктивность, так же пропорциональная его длине; так же вводят удельную индуктивность.

23

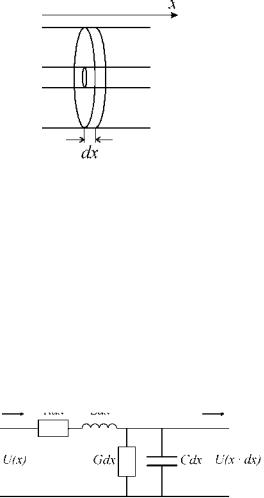
На предыдущих лекциях мы изучали, что емкости и индуктивности реактивных элементов существенно сказываются на переменных во времени процессах, происходящих в электрических цепях. Здесь мы имеем аналогичную ситуацию с той лишь разницей, что реактивные элементы не сосредоточены в отдельных элементах, а распределены вдоль всей длины кабеля.

Дадим определение: длинная линия - система из двух и более параллельных проводников, длина которых во много раз превышает длину волны распространяющихся в ней электромагнитных колебаний, а расстояние между проводниками, в свою очередь, значительно меньше этой длины волны. Забегая вперед, отметим, что при нарушении второго условия электромагнитные волны могут распространяться под углом к направлению проводников линии. Такие волны быстро затухают по мере движения вдоль линии, и динамика и скорость затухания в сильной степени определяются их частотой, т.е. их рассмотрение есть другая, значительно более сложная задача.

В дальнейшем будем рассматривать однородные линии, все параметры которых не изменяются вдоль их длины.

Рисунок 24. Выделение малого отрезка коаксиального кабеля.

Рассмотрим малый отрезок кабеля с удельной емкостью С и удельной индуктивностью L длиной dx, как показано на рисунке 24. У этого отрезка есть емкость Cdx и индуктивность Ldx. Кроме того активные потери при протекании тока по жиле и оплетке можно рассмотреть, если ввести удельное сопротивление линии R. Так же можно рассмотреть случай неидеального (слегка проводящего) диэлектрика, введя удельную проводимость G между жилой и оплеткой. Тогда сопротивление отрезка кабеля равно Rdx, проводимость - Gdx. Получающаяся при этом эквивалентная схема малого отрезка кабеля представлена на рисунке 25.

24

dU I(x + dx, t) = I(x, t) — IG — Ic = I(x, t) — UGdx — — Cdx,

U(x + dx, t) = U (x, t) — IR — IL = U (x, t) — IRdx — ^ Ldx.

Отсюда легко получаются так называемые телеграфные уравнения - система из дифференциальных уравнений в частных производных, описывающая распространение сигналов в длинных линиях:

dJL=-R,-LdA

дх dt

?L=-CU-cal.

дх dt

Далее будем рассматривать линию без потерь: R = 0, G = 0. Если при этом первое уравнение продифференцировать по х, поменять последовательность дифференцирования и использовать второе уравнение, то получим:

здесь введено обозначение v = 1/^LC. Аналогично получаем

д21 = 1 д21 дх2 v2 dt2:

Решением уравнения является любая функция вида Ut(t — x/v), что можно проверить непосредственно. Это решение представляет собой произвольную волну напряжения, распространяющуюся вдоль оси х в положительном направлении со скоростью V. Вторым независимым решением этого уравнения есть любая функция вида U2(t + x/v). Поскольку это уравнение второго порядка, то у него больше нет независимых решений, и любое его решение представимо в виде:

U(x,t) = U±(t — x/v) + U2(t + x/v).

Аналогично для тока

I(x, t) = I ±(t — x/v) + I2(t + x/v).

Подставим эти решения в первое уравнение системы телеграфных уравнений:

— '^U'1(t — x/v) +^U'2(t + x/v) = —L(/'1(t — x/v) + I'2(t + x/v)). Поскольку

волны независимы, то

Пренебрегая ни на что не влияющими постоянными интегрирования, получаем

Ut = р1г, U2 = — pl2.,

здесь введено волновое сопротивление линии

р = Lv = ^L/C.

25

отражения, от источника, не произойдет. Источник “увидит” эти значения R, и начнет работать на них. Ток от источника будет I = Е/г и 1 = 0 соответственно.

3.Общий случай R Ф р. По линии будут распространяться последовательно отраженные от источника и нагрузки волны, амплитуда тока в которых будет сходиться к I = E/R.

Остается добавить, что не рассмотренные нами потери в линии ведут как к ослаблению распространяющегося сигнала, так и к искажению его формы, поскольку скорость распространения различных составляющих его гармоник становится разной; это явление мы подробно разберем в следующих лекциях.

1.9Квазистационарное приближение. Скинэффект

Запишем систему уравнений Максвелла (с системе единиц СГС)

rotE = --—, divB = 0,

с d t

rotH = — j + -^, div D = 4np.

сс d t

Вправой части этих уравнений стоят источники полей. Можно сказать, что электрическое поле возбуждается электрическими зарядами и изменяющимся во времени магнитным полем, а магнитное поле - изменяющимся во времени электрическим полем. Оказывается, что в очень широком круге явлений членом с dD/dt можно пренебречь. Такое приближение называется квазистационарным.

Вквазистационарном приближении производной dB/dt отнюдь не пренебрегают. На первый взгляд, здесь есть противоречие. Рассмотрим вопрос детальнее. Пусть характерные размеры системы L, а характерное время изменения полей Т. Тогда производные по времени имеют порядок 1/L, а по координатам - 1/Т. Предположим, что производная dB/dt имеет тот же порядок, что с rotE, то есть

cE/L-B/T.

Тогда отношение члена dD/dt к члену с rotH будет порядка

Вспомним, что электромагнитные волны распространяются со скоростью света с (в среде - чуть меньше, но это не важно). Если размеры системы L малы по сравнению с расстоянием сТ, которое пробегает электромагнитная волна за характерное время изменения полей, то вычисленное отношение много меньше единицы, и действительно можно пренебрегать производной 3D/dt, сохраняя в то же время производную dB/dt.

27

Кроме того, член с 3D/dt должен быть много меньше плотности тока свободных зарядов j. Запишем это условие в оценке по порядку величины, используя закон Ома в дифференциальной форме:

D/T ~Е/Т « j = оЕ, То » 1.

Для проводников это условие с запасом выполняется для всех интересующих нас частот.

С физической точки зрения квазистационарное приближение соответствует, с одной стороны, отсутствию запаздывания, связанного с конечным временем распространения электромагнитных волн. С другой стороны, квазистационарное приближение соответствует отсутствию излучения ЭМ волн.

Рассмотрим, какие уравнения можно получить из системы уравнений Максвелла в квазистационарном приближении, если рассматривать поля в проводниках. В проводниках плотность тока свободных полностью определяется токами проводимости j = стЕ; сделаем эту замену в соответствующем уравнении и применим операцию ротора к обеим его частям:

rot rotН = — a rotЕ = —-а —.

ссг d t

Вспоминая одну из формул векторного анализа

rot rot = grad div — A и учитывая, что div В = 0, для однородной среды (д = const) получаем

Аналогичное уравнение для поля Е получается при исключении из системы уравнений Максвелла магнитного поля

при условии равенства нулю плотности свободных зарядов. Подобными уравнениями, только для скалярного поля, описываются диффузионные процессы, в частности, теплопроводность.

Рассмотрим пример - длинный проводящий цилиндр, который погружен в стационарное и однородное магнитное поле, направленное вдоль его оси. Пусть в нулевой момент времени это поле достаточно быстро выключают. Внутри цилиндра магнитное поле также начинает уменьшаться во времени, но возникающие в толще проводника вихревые токи препятствуют его быстрому ослаблению. Потом, постепенно, эти токи затухают, и поле внутри цилиндра затухает вместе с ними. Оказывается, задача уменьшения поля в цилиндре равнозначна задаче остывания равномерно нагретого цилиндра! Диффузия тепла из внутренних областей вызывает изменение температуры со временем как показано на рисунке 27.

28

Тогда каждая компонента комплексной амплитуды электрического поля должна в проводнике удовлетворять уравнению

Ј,i(z) = Јile+*z + Јi2e-fez.

Первый член полученного решения описывает поле, экспоненциально возрастающее вглубь проводника. Очевидно, такое решение не имеет физического смысла, и необходимо принять Eit = 0.

Направим другую ось (скажем, х) вдоль вектора Е0. Тогда, исходя из граничных условий на поверхности проводника, компоненты поля равны:

Ёу(0) = fiz(0) = 0, Ёх{0) = Е0.

Отсюда окончательно получаем решение задачи: E(z) = E0e~z/se~lz/s,

E(z) = Е Oe~z/Scos(wt — z/8).

По мере проникновения в проводник амплитуда поля экспоненциально затухает, а само оно начинает все более отставать по фазе от поля вне проводника. Это физическое явление локализации переменного поля в поверхностном слое называется скин-эффектом, а характерная глубина этого слоя 8 - глубиной скин-слоя. Например, при частоте 50 Гц глубина скин-слоя для меди составит 10 мм, алюминия - 7.5 мм, а железа - только 1 мм.

Подобный эффект наблюдается и при рассмотрении задач теплопроводности, что неудивительно, поскольку эти явления описываются одинаковыми уравнениям. Например, вспомним, что колебания температуры в погребе гораздо меньше, чем на поверхности, а время наступления максимальной и минимальной температуры - смещено.

1.10 Поток энергии электромагнитного поля

На предыдущих курсах были получены выражения для плотности энергии электрического и магнитного поля:

В случае электромагнитного поля, как видно из приведенных ранее уравнений Максвелла, изменяющееся электрическое поле порождает в окружающем пространстве изменяющееся магнитное поле, оно - опять порождает электрическое и т.д. Поля распространяются в пространстве, неся с собой энергию, соответственно, можно говорить о плотности потока энергии электромагнитного поля.

30