All lectures pdfs / Ур.мат.физ / Lecture_4 / 2010-09-18 / Лекция_4

- два семейства характеристик исходного уравнения.

Если в исходном уравнении перейти к новым переменным (т. наз. каноническим переменным или характеристическим

то волновое уравнение перепишется так

u»´ = 0:

Для этого уравнения легко находится общее решение

u = F (») + G(´);

где F; G - произвольные функции.

Возвращаясь снова к старым переменным, получим общее решение исходного уравнения

u = F (x + t) + G(x ¡ t):

Поскольку линии t = const не являются характеристиками (в этом

случае °: ª(t; x) = t ¡ t0 и ª2t ¡ ª2x 6= 0), то задача Коши

(

utt ¡ uxx = 0;

ujt=t0 = '0(x); utjt=t0 = '1(x)

поставлена хорошо (корректно поставлена), т.е. по крайней мере к этой задаче применима теорема Коши-Ковалевской о существовании единственного аналитического решения.

2) Возьмем волновое уравнение, записанное в канонических переменных

uxy = f(x; y);

характеристическое уравнение которого имеет вид:

ªxªy = 0 (° : ª(x; y) = 0):

Общее решение

8

><ª = F(y)

>или

:ª = F(x); где F - произвольная функция, т.е. характеристиками являются прямые

y = const или x = const:

y

y=const

x

0

x=const

Общее решение исходного уравнения имеет вид:

Zx Zy

u = d» f(»; ´)d´ + F (x) + G(y);

00

F; G - произвольные, достаточно гладкие функции (не обязательно аналитические).

Будем теперь искать решение задачи Коши

(

uxy = f(x; y);

ujy=0 = '0(x); uyjy=0 = '1(x):

Для этого воспользуемся формулой общего решения. Попытаемся подобрать функции F; G так, чтобы выполнялись условия при

y = 0, а именно:

8

<F (x) + G(0) = '0(x);

Z x

:f(»; 0)d» + G0(0) = '1(x);

0

#

f(x; 0) = '01(x)

::::::::::::::::::::

т.е. F (x) = '0(x) ¡ G(0), а функция G(y) не определяется из этих равенств. Следовательно, при произвольных '0; '1(x) задача Коши не имеет решения. Если же f(x; 0) ´ '01(x), то решение задачи Коши существует, но не единственное, поскольку оно записывается

так:

Zx Zy

u = d» f(»; ´)d´ + '0(x) + G(y) ¡ G(0);

00

где G(y) - произвольная дважды непрерывно дифференцируемая функция, удовлетворяющая условию:

G0(0) = '1(0):

Конечно, это произошло из-за того, что линия y = 0,на которой ставятся данные Коши - характеристика.

3)

utt = ¢xu; x 2 Rn;

° : ª(t; x) = 0 ¡ уравнение характеристики:

ªt = §jrªj ¡ уравнения Гамильтона-Якоби (см. §2). Частные решения:

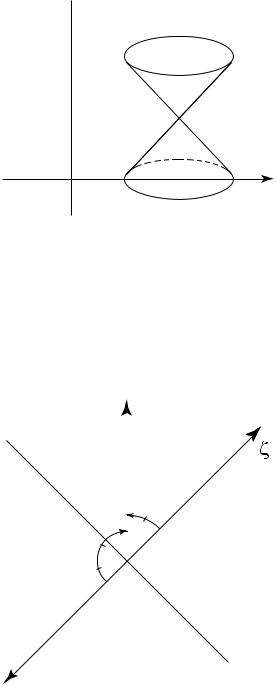
(t ¡ t0)2 ¡ jx ¡ x0j2 = 0 ¡ коническая поверхность

(конус с центром в точке y0 = (t0; x0)).

t

Плоскость (t ¡ t0)³0¤ + (x ¡ x0; ³b¤) = 0, ³¤ = (³0¤; :::; ³n¤) = (³0¤; ³b¤) - нормаль к плоскости, причем ³1¤2 + ::: + ³n¤2 = ³¤2.

Если взять j³¤j = 1, то

4)

rxu = 0 - уравнение Лапласа, x 2 Rn; ° : ª(x) = 0 - характеристика,

jrªj2 = 0 - т.е. уравнение Лапласа не имеет характеристических поверхностей (нет вещественных характеристик).

Следовательно, задача Коши для уравнения

¢x;yu = uxx + uyy = 0

с данными на любой аналитической линии

ª(x; y) = 0

поставлена корректно в классе аналитических функций. 5)

ut = ¢xu; x 2 Rn - уравнение теплопроводности ° : ª(t; x) = 0 - характеристика,

jrªj2 = 0 ! ªxk = 0 ! ª = F(t) ! t = const - характеристики.

Значит задача Коши

(

ut = uxx; x 2 R1;

ujt=0 = '0(x); utjt=0 = '1(x)

поставлена некорректно. Другое соображение: задача переопределена. Однако, позже мы установим, что задача

уже хорошо поставлена (эту задачу тоже называют задачей Коши).

Зададимся вопросом: применима ли теорема Коши-Ковалевской (см. §3) к этой задаче. Видно, что непосредственно не применима. Более того, теорема Коши-Ковалевской просто не может быть обобщена на уравнения вида ut = uxx. С этой целью мы приведем пример аналитической функции '0(x), для которой не существует аналитического по t; x решения задачи (¤) (так называемый пример Ковалевской). Это будет означать, что класс аналитических функций уже не является классом корректности для этой задачи.

Пусть

'0(x) = (1 + x2)¡1 = 1 ¡ x2 + x4 ¡ ::: = = X1 u0kxk = X1 u0;2mx2m;

k=0 m=0

Предположим, что существует решение задачи (¤) аналитическое в окрестности начала координат:

и ряд сходится в некоторой окрестности точки (0; 0). Подставляя этот ряд в уравнение ut = uxx, мы получим рекуррентное соотношение на коэффициенты ряда

X1

ut = (j + 1)uj+1;ktjxk = uxx = j;k=0

X1

= (k + 2)(k + 1)uj;k+2tjxk;

j;k=0

т.е.

(j + 1)uj+1;k = (k + 2)(k + 1)uj;k+2; j; k ¸ 0

Поверхность ° : ª(t; x) = 0 называется характеристикой квазилинейного уравнения для данного решения u = u(t; x) этого урав-

u»´ = 0 ! (u»Z)´ = 0 ! u» = F1(») !

! u = F1(»)d» +Q(´):

| {z }

F (»)

(D02 ¡ Dx2)u = 0 ! (D0 ¡ Dx) (|D0 +{zDx)u} = 0:

v

(D0 ¡ Dx)v = 0 ! vt ¡ vx = 0 ! v = f(x + t);

(D0 + Dx)u = v ! ut + ux = v ! ut + ux = f(x + t):