
All lectures pdfs / Ур.мат.физ / Lecture_14 / 2011-03-01 / Лекция_14
.pdf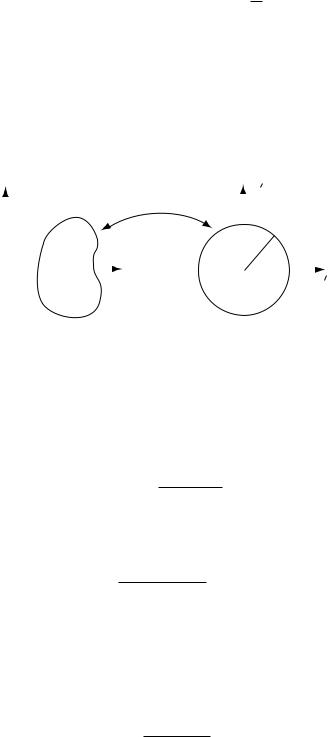
1
§14 Функция Грина задачи Дирихле
Рассмотрим теперь общую ситуацию: ищется решение задачи Di в произвольной области - (- ½ Rn - ограниченная область). Вначале я напомню из ТФКП ситуацию при n = 2. Пусть z0 = F (z), z = x1 +ix2, z0 = x01 +ix02 - аналитическая в - и непрерывно дифференцируемая (по x1, x2) в - функция, осуществляющая взаимно-однозначное отображение области - на круг jx0j < R (jz0j < R) радиуса R = jF (z)j, z 2 @-. Пусть u(z) = u(x) - классическое решение задачи
Di:
|
|
|
4xu = 0; x |
2 |
-; |
(1) |
|||
где '(x) 2 C(@-); |
½ uj@- = '(x); |
|
|
|
|||||
|
|
|
|
|
|
|
|||
u0(z0) = u0(x0)- классическое решение задачи Di: |
|
|
|||||||
|
|
x |
|
|
|
|
|
x2 |
|
|
2 |
|
z =F(z) |
|
|
|
|
||
|
|
|
|
|
|
|
|
||
0 |
|
|
|
|
|
0 |
R |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
x |
|||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
x0u0 |
= 0; |
j |
z0 |
j |
< R; |
|
|
|
||||
|
4 |
|
|
|
|
|
|
|
|
|
|||
½ u0jjz0j=R = ª(z0); |
|
|
|
|
|
||||||||
где ª(z0) = '(F¡1(z0)), F¡1(F (z)) ´ z, z 2 -. |
|
|
|
|
|
||||||||
Согласно формуле (14) из x13 решение задачи (2) |
дается |
||||||||||||
сона: |
1 |
|
Z |
R2 ¡ jz0j2 |
|
|
|
|
|||||
u0(z0) = |
|
ª(³0) d³0 |
j |
; |
|||||||||
2¼R |
jz0 ¡ ³0j2 |
||||||||||||
|
j |
|
|
||||||||||
j³0j=R
(2)
формулой Пуас-
(3)
поскольку ядро Пуассона PR(x0; »0) = PR(z0; ³0) при n = 2 равно:
PR(z0; ³0) = |
R2 ¡ jz0j2 |
; ¾2 = 2¼: |
|
2¼Rjz0 ¡ ³0j2 |
|||
|
|
В силу следствия из теоремы 7 x12
u(z) = u(F¡1(z0)) = u0(z0) = u0(F (z)):
Следовательно, решение задачи (1) дается формулой, которая получается из (3):
u(z) = u0(F (z)) = |
1 |
|
@R- |
R2¡jF (z)j22 |
F 0(³) |
|
'(³) d³ = |
|
||||
2¼R |
|
|
|
|||||||||
|
|
|
|
|
jF (z)¡F (³)j j |
|
j ¢ |
¢ j j |
(4) |
|||
1 |
@R- |
jF (³)j2¡jF (z)j2 |
|
|
||||||||
= |
2¼ |
jF (³)j¢jF (z)¡F (³)j2 |
jF 0(³)j ¢ '(³) ¢ jd³j; |
|
|
|
||||||
поскольку R = jF (³)j, ³ 2 @-, jd³0j = jF 0(³)jjd³j (³0 |
= F (³)). |
|
||||||||||
Таким образом, вопрос о решении задачи Di для уравнения Лапласа при n = 2 решается до конца, если найдено конформное преобразование, переводящее данную область - ½ R2 в круг. Заметим однако, что задача о нахождении такого преобразования не проще исходной задачи Di.
Пусть теперь n > 2 и - ½ Rn - произвольная ограниченная область. Если посмотреть внимательно все рассуждения, приводящие нас к формуле (14) из x13, то можно сделать следующие обобщающие выводы.
Определение.
2
Функцией Грина задачи Di для области - называется функция G(x; y), x 2 -, y 2 -, удовлетворяющая следующим свойствам:
1) 8y 2 -
G(x; y) = g(x; y) ¡ U(x ¡ y); |
(5) |
||
где функция g(x; y) - гармоническая в - и непрерывная на |
- |
по x; |
|
2) 8y 2 - |
(6) |
||
G(»; y)j»2@- = 0: |
|||
Из условий (5), (6) следует:
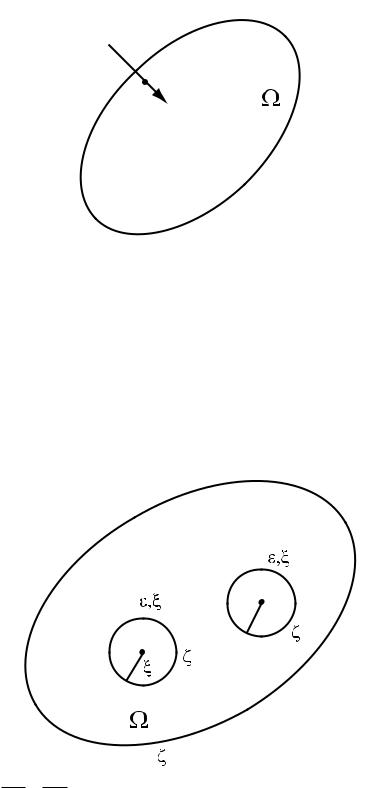
а) G(x; y) - гармоническая по x в области - n fyg;
б) G(x; y) - непрерывная функция по x в области -nfyg, причем G(x; y) ! +1 при x ! y и G(»; y) = 0 при » 2 @-;
в) в силу принципа максимума (см. теорему 8 из x12) G(x; y) > 0 при x 2 -, y 2 -;
-" = - n S";y;
 y
y
доказательство заключается в применении принципа максимума к гармонической функции G(x; y) (по x) в области -".
г) поскольку:
g(»; y) = U(» ¡ y)j»2@- = 0; 8y 2 -; |
(7) |
то g(»; y) < 0 при » 2 @-, y 2 -; следовательно в силу принципа максимума g(x; y) < 0 при x 2 -, y 2 -.
д) функция Грина удовлетворяет неравенствам (см. (5)):
0 < G(x; y) < ¡U(x ¡ y); x 2 -; y 2 -; x 6= y: |
(8) |
е) поскольку функция g(x; y) удовлетворяет задаче Di следующего вида:
4xg(x; y) = 0; x 2 -; |
y 2 -; |
(9) |
½ g(»; y)j»2@- = U(» ¡ y); |
» 2 @-; y 2 -; |
|
то из теоремы 2 (?!) x13 следует, что функция g(x; y) (а вместе с ней и функция Грина G(x; y)) существует; из теоремы 1 этого же параграфа следует, что функция Грина G(x; y) единственна.
Еще одно свойство функции Грина я сформулирую в виде задачи.
Задача.
Покажите, что функция g(x; y) непрерывна по совокупности переменных (x; y) в - £ -.
Замечание.
Надо показать, что jg(x0; y0) ¡ g(x; y)j ! 0, когда (x; y) ! (x0; y0), x; x0 2 -, y; y0 2 -. Затем выписываем очевидное неравенство:
jg(x0; y0) ¡ g(x; y)j < jg(x0; y0) ¡ g(x; y0)j + jg(x; y0) ¡ g(x; y)j
3
и оцениваем каждое слагаемое в правой части (первое слагаемое можно сделать как угодно малым за счет непрерывности функции g(x; y) по x, второе слагаемое - за счет применения принципа максимума (?!)).
Прежде, чем мы сформулируем ещё некоторые свойства функции Грина
G(x; y), я дам определение правильной нормальной производной. Пусть граница области -: @- достаточно гладкая и функция u(x) 2 C1(-). Будем го-
ворить, что функция u имеет правильную нормальную производную на @u(x)
@Nx
на @-, если равномерно по всем x 2 @- существует предел нормальной про-
изводной @u(x0) = (Nx; rx0u(x0)) при x0 ! x, x0 2 ¡Nx.
@Nx
 Nx
Nx
x  x
x
-Nx
Замечание.
Правильная нормальная производная непрерывна на @-, если она существует. Справедлива
Теорема 1.
Если @- - достаточно гладкая поверхность, то функция Грина имеет правиль-
ную нормальную производную @G(»;y) , » 2 @-, y 2 - на @- и симметрична:
@N»
G(x; y) = G(y; x); x 2 -; y 2 -: |
(10) |
Доказательство теоремы 1 мы не будем проводить, ограничимся только замечанием по поводу доказательства свойства (10).
S
S
x
 y
y
-" = - n S";» [ S";x, x 6= »
v(y) = G(y; »), u(y) = G(y; x)
4
Применим к эти функциям в области -" вторую формулу Грина (см. x12):
-R" |
(v(y) |
|
|
yu(y) |
|
|
u(y)4yv(y))dy = 0 = |
|
|||||||
|
|
4 @u(³) |
¡ |
u ³) |
@v(³) |
dS |
+ |
|
|
|
|||||
= |
v ³ |
|
|
|
|
|
|
|
|
||||||
|
@R- f ( |
|
) @N³ |
¡@G((³;x)@N³ g |
³ |
|
@G(³;») |
gdS³+ |
( ) |
||||||
+ |
x |
=" |
fG(³; ») |
|
@N³ |
|
¡ G(³; x) |
@N³ |
¤ |
||||||
|
j³¡Rj |
|
|
|
|
|
@G(³;x) |
|
|
|
@G(³;») |
|
|
||
+j³¡R»j=" fG(³; ») |
|
@N³ |
|
¡ G(³; x) |
@N³ |
gdS³: |
|
||||||||
Затем, подставляя в (¤) представления (см. (5)!):
G(y; ») = g(y; ») ¡ U(y ¡ »); G(y; x) = g(y; x) ¡ U(y ¡ x)
и рассуждая также, как при доказательстве теоремы 1 из x12, в пределе при " ! 0 получим:
g(»; x) = g(x; »);
т.е. выполнено равенство (10).
Замечание.
Из симметрии функции g(x; y) вытекает, что функция g(x; y) непрерывна по совокупности переменных (x; y) в -£-; при 8x 2 -, функция g(x; y) гармоническая по y в -, принимает значение U(x ¡») при » 2 @- и имеет правильную
нормальную производную @g(x;») (x 2 -, » 2 @-) на @-.
@N»
Дальнейшие рассуждения можно сформулировать в виде следующих этапов.
1 этап. Пусть u(x) 2 C2(-). Тогда в силу теоремы 1 из x12 (формула (7))
имеет место представление: |
|
@N¡» |
¡ U(x ¡ ») @N» |
¾dS»: (+) |
|||||
u(x) = Z- |
U(x ¡ y)4yu(y)dy +@Z- ½u(») |
||||||||
|
|
|
@U(x |
») |
|
|
|
@u(») |
|
В силу второй формулы Грина из x12 |
справедливо равенство: |
(++) |
|||||||
0 = Z- |
g(x; y)4yu(y)dy +@Z- ½u(») |
|
@N» |
¡ g(x; ») @N» |
¾dS»: |
||||
|
|
@g(x; ») |
|
|
@u(») |
|
|
|
|
Вычитая из (+) равенство (++) в итоге получим ещё одно представление:
для любой функции u(x) 2 C2(-): |
|
|
|
|
u(x) = ¡@Z- u(») |
@G(x; ») |
dS» ¡ Z- |
G(x; y)4yu(y)dy: |
(11) |
@N» |
||||
2 этап. Доказательство того факта, что представление (11) справедливо
для любой функции u(x) 2 C2(-) \ C( |
|
) |
|
||||||||||
- |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||
- b - (- ½ -) |
|
|
|
|
|
|
|
||||||
" |
= |
max |
@- j |
x |
¡ |
y |
j |
> 0 |
|
|
|
||
e |
|
;y |
|
|
|
|
|
|
|||||
|
x2@-e2 |
|
|
|
|
|
|
|
|
|
|||
3 этап. Если классическое решение задачи Дирихле (Di) |
|
||||||||||||
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4xu = f(x); x 2 -; |
(Di) |
||
|
|
|
|
|
|
|
|
|
|
½ uj@- = '(x); x 2 @- |
|
||
существует (при непрерывной и ограниченной f(x) 2 C(-) и непрерывной
'(x) 2 C(@-)), то оно представляется в виде: |
|
|
||
u(x) = ¡@Z- |
@G(x; ») |
'(»)dS» ¡ Z- |
G(x; y)f(y)dy: |
(12) |
@N» |
||||

5
Затем доказывается, что при f(x) 2 C1(-), '(x) 2 C(@-) формула (12) даёт решение задачи Di.
Замечание.
Метод функций Грина для физиков и вычислителей.
