
Diss / 4
.pdf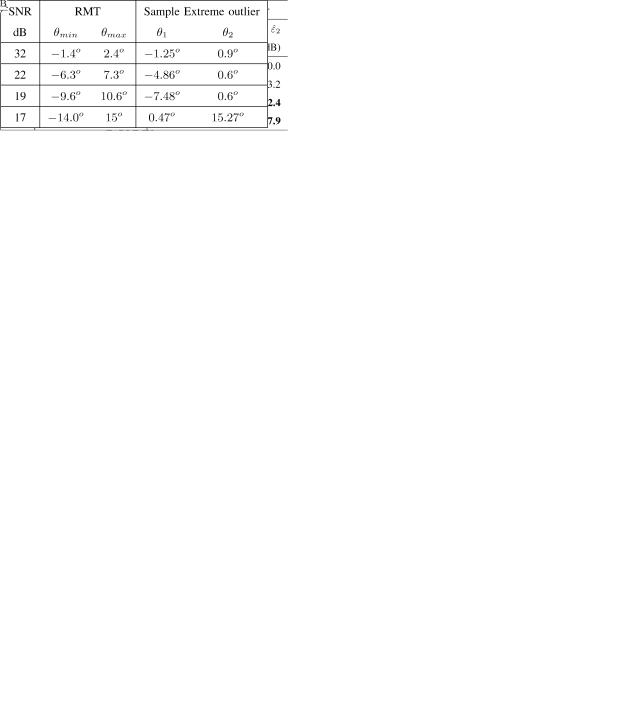
ABRAMOVICH AND JOHNSON: DETECTION–ESTIMATION OF VERY CLOSE EMITTERS |
3657 |
TABLE III
COMPARISON OF THEORETICAL “SINGLE-CLUSTER” NONIDENTIFIABILITY
CONDITION AGAINST ACTUAL SAMPLE EXTREME MLE OUTLIER
TABLE IV




outlier are quite accurately predicted by the “single-cluster” criterion. In order to asses the accuracy of the “single cluster” prediction of “MLE ambiguity region” DOA bounds for each SNR 37, 30, 25, and 22 dB, we examined the trial that generated the extreme outlier in our 1000 Monte-Carlo simulations (Tables I–II) and compared this with the “MLE ambiguity region” predictions, calculated as described in (29).
Table III shows that the single-cluster condition predicts the sample MLE outliers with high accuracy, for scenario with 

















 . Table IV illustrates the similar comparison of the extreme “outliers” recorded over 1000 Monte-Carlo trials with the “single cluster” predictions, for the scenario
. Table IV illustrates the similar comparison of the extreme “outliers” recorded over 1000 Monte-Carlo trials with the “single cluster” predictions, for the scenario 














 SNR
SNR 





 and
and 
 dB. One can see that everywhere the accuracy of the “MLE ambiguity region” prediction is quite high. Note that when applied to a scenario with well resolved sources, the confidence interval calculated using this “single cluster” criterion
dB. One can see that everywhere the accuracy of the “MLE ambiguity region” prediction is quite high. Note that when applied to a scenario with well resolved sources, the confidence interval calculated using this “single cluster” criterion
in the vicinity of the true DOAs |
is in compliance with |
the CRB predictions. |
|
V. SUMMARY AND CONCLUSION
We have reexamined the well-known problem of detectionestimation of closely spaced independent sources. Unlike most of the previous studies, we have conducted direct exhaustive search for the globally optimal MLE solutions and then proposed an RMT-based tool for statistical analysis of the detec- tion-estimation performance in the threshold area.
The major observation made in [20] and [24] regarding the existence of “MLE ambiguity region” at certain SNRs, has been proven. Namely, within the “SNR ambiguity range” 




SNR 



 , where
, where 


 is the SNR where the CRB standard deviation is equal to half of the inter-source separation and
is the SNR where the CRB standard deviation is equal to half of the inter-source separation and 


 is the SNR below which the number of sources is underestimated with high probability, MLE is shown to suffer from
is the SNR below which the number of sources is underestimated with high probability, MLE is shown to suffer from
“breakdown” which is producing a severely erroneous DOA estimate. Within this “SNR ambiguity range,” two sources are properly detected, but the ML DOA estimates are such that one of them is “good,” while the other is an outlier. The second source is an outlier that is distributed randomly within an MLE ambiguity region that depends on SNR and sample support for the given scenario. Analytical description of this MLE ambiguity region was another major goal of this paper. The need for this analytical description is important not only from the theoretical, but also from the practical standpoint. While obviously no expectations on successful ML DOA estimation below 


 limit existed, we also discovered that at SNR values that exceed the CRB threshold, the traditional (asymptotic) description of MLE errors by the multivariate Gaussian pdf with FIM-inverse as a covariance matrix, remains poor in predicting bounds, particularly for small values of
limit existed, we also discovered that at SNR values that exceed the CRB threshold, the traditional (asymptotic) description of MLE errors by the multivariate Gaussian pdf with FIM-inverse as a covariance matrix, remains poor in predicting bounds, particularly for small values of  . Therefore, the derived analytical bounds for the “MLE ambiguity region” serve as important complement to the CRB, that for SNR
. Therefore, the derived analytical bounds for the “MLE ambiguity region” serve as important complement to the CRB, that for SNR 



 calculates the RMSE of the ML DOA estimate, but fail to properly represent its confidence interval.
calculates the RMSE of the ML DOA estimate, but fail to properly represent its confidence interval.
The main idea in our analytical derivations was that for a given covariance matrix  , we tried to find an “extreme” covariance matrix model
, we tried to find an “extreme” covariance matrix model 







 or
or 








 that for a given sample volume
that for a given sample volume  , is statistically indistinguishable from the true covariance matrix
, is statistically indistinguishable from the true covariance matrix  . We exploited the RMT G-asymp- totic
. We exploited the RMT G-asymp- totic 









 deterministic description of the sample distributions of eigenvalues of random matrices. In particular, we “inverted” a theorem on the “eigenvalue splitting condition” to formulate our “single cluster” condition on all empirical eigenvalues of a random matrix
deterministic description of the sample distributions of eigenvalues of random matrices. In particular, we “inverted” a theorem on the “eigenvalue splitting condition” to formulate our “single cluster” condition on all empirical eigenvalues of a random matrix  to belong to a single cluster.
to belong to a single cluster.
In a number of important cases, this criterion led to the analytical expressions. In particular, we demonstrated that the derived expressions that specify the sample volume  , beyond which a given two-source model becomes indistinguishable from the “best” single-source model, very accurately followed the attempted Monte-Carlo simulations. The same accuracy of our analytic expression was demonstrated for the ITC detection threshold
, beyond which a given two-source model becomes indistinguishable from the “best” single-source model, very accurately followed the attempted Monte-Carlo simulations. The same accuracy of our analytic expression was demonstrated for the ITC detection threshold 


 .
.
To address the problem of finding the DOA bounds in the MLE ambiguity region we suggested computationally manageable (one-dimensional search) procedure to find the extreme DOA sets 






 and
and 





 that still met the single cluster criterion. Comparison of the RMT prediction results with the conducted Monte-Carlo simulations has demonstrated the remarkable accuracy of the MLE ambiguity region prediction,
that still met the single cluster criterion. Comparison of the RMT prediction results with the conducted Monte-Carlo simulations has demonstrated the remarkable accuracy of the MLE ambiguity region prediction,
both for the “practical” SNR range SNR |
, and well deep |
|
into the SNR ambiguity range |
SNR |
. |
Therefore, the introduced RMT-based methodology may complement the CRB analysis for the DOA estimation error analysis in the “practical” range SNR 



 , and complement or even replace the much more complicated “large error” Barankin bounds [17]–[19] within the “SNR ambiguity range” and beyond. While the prediction of MLE threshold behavior for a given scenario is now addressed, in fact we are left with an important unresolved practical problem. Indeed, in practical case, using ITC-MLE or GLRT-based detection-estimation we may frequently generate two DOA estimates with different
, and complement or even replace the much more complicated “large error” Barankin bounds [17]–[19] within the “SNR ambiguity range” and beyond. While the prediction of MLE threshold behavior for a given scenario is now addressed, in fact we are left with an important unresolved practical problem. Indeed, in practical case, using ITC-MLE or GLRT-based detection-estimation we may frequently generate two DOA estimates with different

3658 |
IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 58, NO. 7, JULY 2010 |
powers for reliably detected 

 sources. The estimated model
sources. The estimated model 








 will pass the likelihood ratio test (8) and therefore may be treated as sufficiently “likely.” At the same time, an attempt to retain a single most powerful estimate, say
will pass the likelihood ratio test (8) and therefore may be treated as sufficiently “likely.” At the same time, an attempt to retain a single most powerful estimate, say 




 if
if 



 , will produce a model that is not likely enough for the “detector-estimator” (8). For the conventional “ITC-MLE” algorithm it is not even an option, if
, will produce a model that is not likely enough for the “detector-estimator” (8). For the conventional “ITC-MLE” algorithm it is not even an option, if 

 sources are detected. It is clear that within the MLE/EL paradigm, it is impossible to replace MLE-produced outlier by a “proper” DOA estimate, as we did with the MUSIC-specific outliers in, e.g., [24]. What may be possible, at most, is to establish that the generated MLE result is “MLE ambiguous,” and to identify the least “reliable” ML DOA estimate (an outlier). We intend to address this problem in foreseeable future. Finally, note that generalization of these results to scenarios with more than
sources are detected. It is clear that within the MLE/EL paradigm, it is impossible to replace MLE-produced outlier by a “proper” DOA estimate, as we did with the MUSIC-specific outliers in, e.g., [24]. What may be possible, at most, is to establish that the generated MLE result is “MLE ambiguous,” and to identify the least “reliable” ML DOA estimate (an outlier). We intend to address this problem in foreseeable future. Finally, note that generalization of these results to scenarios with more than 

 sources may not be straightforward in every aspect and should be exercised with care.
sources may not be straightforward in every aspect and should be exercised with care.
APPENDIX A
For the two-source scenario
(A.1)
the eigenvalues and eigenvectors are analytically derived in [42]. In particular, the three different eigenvalues are equal to
|
|
|
(A.2) |
where |
has multiplicity |
and |
are the |
nonzero eigenvalues of the “noise-free” covariance matrix 
(A.3)
equal to 





(A.4)
with 

 as
as 







 . As
. As 







 , the two corresponding eigenvectors of
, the two corresponding eigenvectors of  tend to their asymptotic representation [42]
tend to their asymptotic representation [42]
(A.5)
where
for 








 for
for 





 (A.6)
(A.6)
Therefore, for the covariance matrix 

(A.7)
the eigenvalues of the matrix 
(A.8)
are
(A.9)
We need to find the 


 corresponding to the “eigenvalue splitting condition” given in [27] and [28]
corresponding to the “eigenvalue splitting condition” given in [27] and [28]
(A.10)
and where  denotes the
denotes the 




 real-valued solutions of the equation
real-valued solutions of the equation
(A.11)
which in our case is
(A.12)
Since we are searching for a real-valued solution that in this case is within the range
(A.13)
we get the equation
(A.14)
or equivalently
(A.15)
which finally leads to solution
(A.16)
Now we can calculate 


 , using (A.10)
, using (A.10)
(A.17)
(A.18)
according to (A.14)
(A.19)
therefore we get
(A.20)

ABRAMOVICH AND JOHNSON: DETECTION–ESTIMATION OF VERY CLOSE EMITTERS |
3659 |
with respect to (A.19) we finally get |
similarly to (A.19)–(A.22) we get |
||||||||||||
|
|
|
|
|
|
(A.21) |
|
|
|
|
|
|
(B.9) |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|||||||||||
Finally, we get
(A.22)
(B.10)
APPENDIX B
Here we specify “splitting condition” between the noise sub-
space eigenvalue |
with multiplicity |
, |
|||
and the smallest signal subspace eigenvalue |
in |
||||
. |
|
|
|
|
|
First, let us specify |
as the minimal solution to the (A.11) |
||||
|
|
|
|
|
(B.1) |
|
|
|
|
|
|
(B.2)
In a more general case, when the smallest signal subspace eigenvalue is close to the noise power, i.e.,
(B.11)
where 
 has multiplicity
has multiplicity 




 with
with 




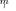

 we get
we get
(B.12)
(B.13)
The smallest  is searched for within the interval
is searched for within the interval 





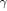
 and since
and since 

 , the contribution of the third member in (B.2) may be ignored because
, the contribution of the third member in (B.2) may be ignored because
(B.3)
while in the vicinity of the solution 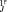 , both other members significantly exceed 1. Therefore, the minimal solution of (B.2) can be found as
, both other members significantly exceed 1. Therefore, the minimal solution of (B.2) can be found as
(B.4)
that similarly to (A.16) leads to the solution
(B.5)
Now, according to (A.10)
(B.6)
which in this case is equal to
(B.7)
since 
 and
and 


 , we get
, we get
(B.8)
(B.14)
that leads to the final expression
(B.15)
ACKNOWLEDGMENT
The authors would like to thank Dr. Mestre for advice on his recent RMT results that we relied on, as well as the reviewers for their very important comments and recommendations. In addition, the authors would like to acknowledge the contributions of N. Spencer, who generated the numerical results.
REFERENCES
[1]A. Steinhardt and C. Bretherton, “Thresholds in frequency estimation,” in Proc. ICASSP-85, 1985, pp. 1273–1276.
[2]D. Tufts, A. Kot, and R. Vaccaro, “The threshold analysis of SVD-based algorithms,” in Proc. ICASSP-88, New York, 1988, pp. 2416–2419.
[3]M. Kaveh and H. Wang, “Threshold properties of narrow-band signalsubspace array processing methods,” in Advances in Spectrum Analysis and Array Processing, S. Haykin, Ed. Englewood Cliffs, NJ: Pren- tice-Hall, 1991, vol. II, ch. 5.
[4]D. Tufts, A. Kot, and R. Vaccaro, “The threshold effect in signal processing algorithms which use an estimated subspace,” in SVD and Signal Processing II: Algorithms, Analysis and Applications, R. Vaccaro, Ed. New York: Elsevier, 1991, pp. 301–320.
[5]J. Thomas, L. Scharf, and D. Tufts, “The probability of a subspace swap in the SVD,” IEEE Trans. Signal Process., vol. 43, no. 3, pp. 730–736, Mar. 1995.
[6]M. Hawkes, A. Nehorai, and P. Stoica, “Performance breakdown of subspace-based methods: Prediction and cure,” in Proc. ICASSP-01, Salt Lake City, UT, 2001, vol. 6, pp. 405–408.
[7]F. Athley, “Threshold region performance of maximum likelihood direction of arrival estimators,” IEEE Trans. Signal Process., vol. 53, no. 4, pp. 1359–1373, Apr. 2005.

3660
[8]C. Richmond, “Mean-squared error and threshold SNR prediction of maximum-likelihood signal parameter estimation with estimated colored noise covariances,” IEEE Trans. Inf. Theory, vol. 52, no. 5, pp. 2146–2164, May 2006.
[9]A. Amar and A. Weiss, “Fundamental resolution limits of closely spaced random signals,” IET Radar Sonar Navig., vol. 2, no. 3, pp. 170–179, 2008.
[10]A. Amar and A. Weiss, “Fundamental limitations on the resolution of deterministic signals,” IEEE Trans. Signal Process., vol. 56, no. 11, pp. 5309–5318, Nov. 2008.
[11]B. Quinn and P. Kootsookos, “Threshold behavior of the maximum likelihood estimator of frequency,” IEEE Trans. Signal Process., vol. 42, no. 11, pp. 3291–3294, Nov. 1994.
[12]P. Forster, P. Larzabal, and E. Boyer, “Threshold performance analysis of maximum likelihood DOA estimation,” IEEE Trans. Signal Process., vol. 52, no. 11, pp. 3183–3191, Nov. 2004.
[13]D. Rife and R. Boorstyn, “Single tone parameter estimation from dis- crete-time observations,” IEEE Trans. Inf. Theory, vol. IT-20, no. 5, pp. 591–598, Sep. 1974.
[14]B. James, B. Anderson, and R. Williamson, “Characterization of threshold for single tone maximum likelihood frequency estimation,” IEEE Trans. Signal Process., vol. 43, no. 4, pp. 817–821, Apr. 1995.
[15]F. Athley, “Performance analysis of DOA estimation in the threshold region,” in Proc. ICASSP-02, Orlando, FL, 2002, vol. 3, pp. 3017–3020.
[16]C. Richmond, “On the threshold region mean-squared error performance of maximum-likelihood direction-of-arrival estimation in the presence of signal model mismatch,” in Proc. Sens. Array and Multichannel Signal Processing Workshop, Boston, MA, 2006, pp. 268–272.
[17]I. Reuven and H. Messer, “The use of the Barankin bound for determining the threshold SNR in estimating the bearing of a source in the presence of another,” in Proc. ICASSP-95, Detroit, MI, 1995, vol. 3, pp. 1645–1648.
[18]E. Barankin, “Locally best unbiased estimates,” Ann. Math. Statist., vol. 20, no. 4, pp. 477–501, 1949.
[19]E. Chaumette, J. Galy, A. Quinlan, and P. Larzabal, “A new Barankin bound approximation for the prediction of the threshold region performance of maximum likelihood estimators,” IEEE Trans. Signal Process., vol. 56, no. 11, pp. 5319–5333, Nov. 2008.
[20]H. Lee and F. Li, “Quantification of the difference between detection and resolution thresholds for multiple closely spaced emitters,” IEEE Trans. Signal Process., vol. 41, no. 6, pp. 2274–2277, Jun. 1993.
[21]S. Smith, “Statistical resolution limits and the complexified
Cramér–Rao bound,” IEEE Trans. Signal Process., vol. 53, no. 5, pp. 1597–1609, May 2005.
[22]M. Kaveh and A. Barabell, “The statistical performance of the MUSIC and the minimum-norm algorithms in resolving plane waves in noise,” IEEE Trans. Signal Process., vol. SP-34, no. 2, pp. 331–341, Feb. 1986.
[23]Y. Abramovich and N. Spencer, “DOA estimation performance breakdown: A new approach to prediction and cure,” in Proc. EUSIPCO-02, Toulouse, France, 2002, vol. 1, pp. 89–92.
[24]Y. Abramovich, N. Spencer, and A. Gorokhov, “GLRT-based threshold detection-estimation performance improvement and application to uniform circular antenna arrays,” IEEE Trans. Signal Process., vol. 55, no. 1, pp. 20–31, Jan. 2007.
[25]Y. Abramovich and N. Spencer, “Performance breakdown of subspacebased methods in arbitrary antenna arrays: GLRT-based prediction and cure,” in Proc. ICASSP-04, Montreal, QC, Canada, 2004, vol. 2, pp. 117–120.
[26]J.-J. Fuchs, “On the application of the global matched filter to DOA estimation with uniform circular arrays,” IEEE Trans. Signal Process., vol. 49, no. 4, pp. 702–709, Apr. 2001.
[27]X. Mestre, “On the asymptotic behaviour of the sample estimates of eigenvalues and eigenvectors of covariance matrices,” IEEE Trans. Signal Process., vol. 56, no. 11, pp. 5353–5368, Nov. 2008.
[28]V. Girko, An Introduction to Statistical Analysis of Random Arrays. Utrecht, The Netherlands: VSP, 1998.
[29]B. Ottersten, M. Viberg, P. Stoica, and A. Nehorai, “Exact and large sample maximum likelihood techniques for parameter estimation and detection in array processing,” in Radar Array Processing, ser. Springer Series in Information Sciences, S. Haykin, J. Litva, and T. Shepherd, Eds. Berlin: Springer-Verlag, 1993, vol. 25, ch. 4, pp. 99–151.
[30]B. A. Johnson and Y. I. Abramovich, “DOA estimator performance assessment in the pre-asymptotic domain using the likelihood principle,”
Elvesier J. Signal Process., vol. 90, pp. 1–10, 2009.
[31]Y. Abramovich, N. Spencer, and A. Gorokhov, “Bounds on maximum likelihood ratio—Part I: Application to antenna array detection-estima- tion with perfect wavefront coherence,” IEEE Trans. Signal Process., vol. 52, no. 6, pp. 1524–1536, Jun. 2004.
IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 58, NO. 7, JULY 2010
[32]Y. Abramovich, N. Spencer, and A. Gorokhov, “Bounds on maximum likelihood ratio—Part II: Application to antenna array detection-es- timation with imperfect wavefront coherence,” IEEE Trans. Signal Process., vol. 53, no. 6, pp. 2046–2058, Jun. 2005.
[33]B. Porat, Digital Processing of Random Signals, 5th ed. Englewood Cliffs, NJ: Prentice-Hall, 1994.
[34]P. Djuric´, “A model selection rule for sinusoids in white Gaussian noise,” IEEE Trans. Signal Process., vol. 44, no. 7, pp. 1744–1757, Jul. 1996.
[35]M. Rendas and J. Moura, “Ambiguity in radar and sonar,” IEEE Trans. Signal Process., vol. 46, no. 2, pp. 294–305, Feb. 1998.
[36]Y. Abramovich, V. Gaitsgory, and N. Spencer, “Stability of manifold ambiguity resolution in DOA estimation with nonuniform antenna arrays,” AEÜ Int. J. Electron. Commun., vol. 53, no. 6, pp. 364–370, 1999.
[37]A. Renaux, P. Forster, E. Boyer, and P. Larzabal, “Unconditional maximum likelihood performance at finite number of samples and high signal-to-noise ratio,” IEEE Trans. Signal Process., vol. 55, no. 5, pp. 2358–2364, May 2007.
[38]R. Muirhead, Aspects of Multivariate Statistical Theory. New York: Wiley, 1982.
[39]Y. Abramovich, N. Spencer, and A. Gorokhov, “Modified GLRT and AMF framework for adaptive detectors,” IEEE Trans. Aero. Elect. Sys., vol. 43, no. 3, pp. 1017–1051, Jul. 2007.
[40]V. Marcˆenko and L. Pastur, “Distribution of the eigenvalues in certain sets of random matrices,” (in Russian) Mat. Sb., vol. 1, pp. 457–483, 1967.
[41]A. Tulino and S. Verdi, Random Matrix Theory in Wireless Communications. Delft, The Netherlands: now Publishers, 2004.
[42]H. van Trees, Optimum Array Processing. New York: Wiley, 2002, vol. 4, in Detection, Estimation, and Modulation Theory.
[43]A. Pezeshki, B. Veen, L. Scharf, H. Cox, and M. Lundberg, “Eigenvalue beamformer using a multi-rank MVDR beamformer and subspace selection,” IEEE Trans. Signal Process., vol. 56, no. 5, pp. 1954–1967, May 2008.
Yuri I. Abramovich (M’96–SM’06–F’08) received the Dipl. Eng. (Hons.) degree in radio electronics in 1967 and the Cand. Sci. degree (Ph.D. equivalent) in theoretical radio techniques in 1971, both from the Odessa Polytechnic University, Odessa (Ukraine), U.S.S.R., and the D.Sc. degree in radar and navigation from the Leningrad Institute for Avionics, Leningrad (Russia), U.S.S.R., in 1981.
From 1968 to 1994, he was with the Odessa State Polytechnic University, Odessa, as a Research Fellow, Professor, and ultimately as Vice-Chancellor
of Science and Research. From 1994 to 2006, he was at the Cooperative Research Centre for Sensor Signal and Information Processing (CSSIP), Adelaide, Australia. Since 2000, he has been with the Australian Defence Science and Technology Organization (DSTO), Adelaide, as Principal Research Scientist, seconded to CSSIP until its closure. His research interests are in signal processing (particularly spatio-temporal adaptive processing, beamforming, signal detection and estimation), its application to radar (particularly over-the-horizon radar), electronic warfare, and communication.
Dr. Abramovich is currently an Associate Editor of the IEEE TRANSACTIONS ON AEROSPACE AND ELECTRONIC SYSTEMS and previously served as Associate Editor of the IEEE TRANSACTIONS ON SIGNAL PROCESSING from 2002 to 2005.
Ben A. Johnson (S’04–M’09–SM’10) received B.Sc. (cum laude) degree in physics from Washington State University, Pullman, in 1984, the M.Sc. degree in digital signal processing from the University of Southern California, Los Angeles, in 1988, and the Ph.D. degree from the University of South Australia, Adelaide, in 2009, focusing on application of spatio-temporal adaptive processing in HF radar.
From 1984 to 1989, he was at Hughes Aircraft Company (now Raytheon) as a Systems Engineer in airborne radar. From 1989 to 1998, he was with
Sensis Corporation as a Senior Radar Engineer in ground-based surveillance systems. Since 1998, he has been with Lockheed Martin Australia Electronic Systems Pty. Ltd. on the Jindalee over-the-horizon Operational Radar Network (JORN), first as a Senior Test Engineer and now as Technical Director. In addition, since 2010 he has been an Adjunct Professor at the University of South Australia.
