I Кривые второго порядка

231

Глава 5

КРИВЫЕ И ПОВЕРХНОСТИ

ВТОРОГО ПОРЯДКА

В этой главе мы будем обсуждать свойства кривых и поверхностей,

которые задаются в декартовой системе координат алгебраическими уравнениями второй степени. Изучение этих геометрических объек-

тов традиционно начинают с исследования свойств трех кривых —

эллипса, гиперболы и параболы.

5.1.Эллипс

●Вывод уравнения эллипса

Определение 5.1. Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух задан-

ных точек плоскости (фокусов) есть величина постоянная.

Постоянную величину, которая участвует в определении эллип-

са, обозначают символом 2a.

► Выберем декартову систему координат следующим образом. Ось абсцисс проведем через фокусы эллипса ( точки F1 и F2 ), а начало системы координат расположим в середине отрезка F1F2 (рис. 5.1) .

Предположим, что длина отрезка F1F2 равна 2c. Тогда точки F1 и

F2 в заданной системе координат имеют координаты F1( c,0)и

F2(c,0). Пусть M(x;y) есть произвольная точка эллипса, r1 и r2 —

расстояния от M до точек F1 и F2 соответственно.

y

Рис. 5.1.

Согласно определению 5.1, для любой точки M(x;y) эллипса вы-

полняется равенство

ипосле элементарных алгебраических преобразований получим

x2 2xc c2 y2

4a2 4a(x c)2 y2 x2 2xc c2 y2

Очередное возведение в квадрат обеих частей равенства приводит к равенству:

a2((x c)2 y2) a4 2a2xc x2c2 , a2(x2 2xc c2 y2) a4 2a2xc x2c2 ,

откуда после раскрытия скобок, приведения подобных членов и группировки слагаемых получим:

ввести обозначение a2 c2 b2 . Тогда равенство (5.7) примет сле-

дующий вид:

Если теперь разделить обе части (5.8) на произведение a2b2 , то по-

лучим уравнение (5.1):

которое называется каноническим уравнением эллипса.

Поскольку при выводе уравнения (5.9) мы дважды использова-

ли процедуру возведения в квадрат, равенство (5.9) представляет собой алгебраическое следствие уравнения (5.2), и теперь необхо-

димо убедиться в том, что наши действия не привели к появлению

«лишних» решений.

Покажем, что любая точка M(x, y), координаты которой удов-

летворяют уравнению (5.9), располагается на эллипсе. Для этого

му

Точно так же получим выражение для расстояния r2 :

Суммируя (5.11) и (5.12) , придем к равенству

r1 r2 2a. ◄

Таким образом , соотношение (5.9) действительно задает эллипс,

определенный его фокальным свойством.

● Построение и исследование формы эллипса

Исследуем форму эллипса, опираясь на его каноническое уравнение:

Прежде всего отметим, что эллипс обладает симметрией относи-

тельно начала и обеих осей координат (главные оси эллипса), по-

скольку его уравнение содержит переменные x и y в четной степе-

ни. Центр симметрии эллипса — начало системы координат — на-

зывается центром эллипса. Точки пересечения эллипса с главными осями называются вершинами эллипса. Величины a и b представ-

ляют собой расстояния от центра до вершин эллипса, так как пола-

гая в (5.13) y 0, получим x a, аналогично, если x 0, то y b . Числа a и b называются полуосями эллипса. Из канони-

ческого уравнения также следует, что точки эллипса не могут рас-

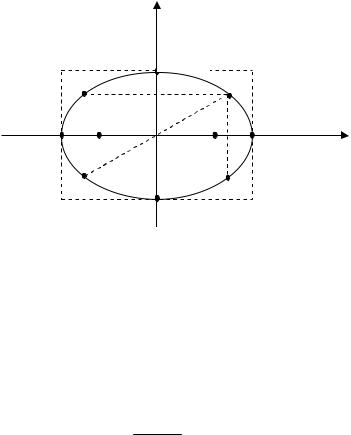
строении эллипса сначала отмечают на осях координат вершины эллипса, затем рисуют пунктирной линией прямоугольник, в кото-

ром должны располагаться точки эллипса, и затем «от руки» прово-

дят кривую (рис. 5.2).

y

B 0,b

a b, то главная ось, образующая в пересечении с эллипсом отре-

зок AC , называется большой осью эллипса, другая главная ось на-

зывается малой осью. Фокусы эллипса – точки F1( c;0) и F2(c;0)

– располагаются на большой оси, внутри прямоугольника (внутри

эллипса), поскольку с a2 b2 a . Если оба фокуса эллипса совпадают (или если a b в каноническом уравнении), то эллипс

превращается в окружность радиуса r a. Вообще говоря, эллипс тесно связан с окружностью. Его даже можно определить, как кри-

вую, которая получена сжатием некоторой окружности к одному из диаметров. Например, сжатие окружности в k раз «вдоль» оси Oy

задается следующим преобразованием системы координат: ~x x ,

Наконец, отметим, что эллипс может быть задан параметрическим уравнением1:

в котором параметр t соответствует углу поворота луча OM

от положительного направления оси Ox (рис. 5.3).

y M

.

x

O

Рис. 5.3

1 Указанное параметрическое уравнение действительно задает эллипс, по-

5.2. Гипербола

Определение 5.2. Гиперболой называется геометрическое место то-

чек плоскости, для каждой из которых модуль разности расстояний до двух заданных точек плоскости ( фокусов ) есть величина посто-

янная.

Так же, как и в случае эллипса, указанную в определении по-

Уравнение (5.15) называется каноническим уравнением гиперболы. ► Выберем декартову систему координат так же, как и в случае эл-

липса (рис. 5.1). В этой системе координат фокусы гиперболы рас-

полагаются в точках F1( c,0) и F2(c,0), и для произвольной точки

M(x, y)гиперболы, согласно (5.3), получим:

240 Глава 5. Кривые и поверхности

поэтому можно догадаться, что гипербола состоит из двух «частей»

— двух ветвей, каждая из которых задается уравнением (5.18) или

(5.19) соответственно. Выберем ветвь гиперболы, связанную с урав-

нением (5.18):

r1 r2 2a ,

Из соотношения (5.17) так же, как в случае эллипса, придем к равен-

ству:

Замечание. В треугольнике F1MF2 модуль разности длин любых двух сторон всегда меньше длины третьей стороны:

r1 r2 F1M F2M 2a F1F2 2c,

поэтому, в отличие от эллипса, для гиперболы всегда справедливо

неравенство a c или c 1. a