-
Терминальные задачи управления.
В
терминальных задачах управления критерий
качества включает в себя терминальную
оценку
,
которая характеризует статические
свойства системы свойства систем, их
ошибки.
Пусть состояние динамической системы
описывается дифференциальным уравнением
вида
=
.
Критерий качества включает в себя
терминальную и интегральную составляющую:
Будем считать, что конечное время не задано, а функция P по крайней мере дважды непрерывно дифференцируема по x и по t.
В силу этого, P можно представить следующим образом:
Подставим это выражение в функционал:
Так как и
заданы, то
=const.
Управление,
минимизирующее данный функционал от
константы не зависит. Следовательно,
данную задачу мы можем рассматривать
как задачу управления с функционалом
(*)
Задача свелась к задаче с интегральным критерием качества, решение которой уже известно. Запишем условие принципа максимума для приведённой задачи.
Пусть
— оптимальный процесс, который переводит
систему из состояния
в
.
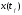Тогда найдётся функция,
и const
,
для которых оптимальная траектория
определяется решением следующей
системыДУ:
Здесь
и
— гамильтониан и допустимая функция
для задачи с критерием качества(*).
Гамильтониан
для приведённой задачи
Также выполняются следующие условия:
1. Условие максимума
2. Условие
трансверсальности
3. Поведение гамильтона вдоль оптимальной траектории
Введём
в расмотрение функцию следующего вида:
С
учётом этой функции H (**) примет следующий
вид
Где H — гамильтониан исходной задачи, который определяется следующим образом:
(***)
Рассмотрим,
какому условию удовлетворяет вектор
(t).
Для этого продифференцируем условие
его по времени:
Таким образом, получили условие (б) для исходной задачи.
Получим условие (а). Из соотношения (***) следует, что
Таким образом, условие (a) также получено.
1. Рассмотрим, какой вид принимает условие максимума по отношению к гамильтониану исходной системы.
Есть условие
для приведённой
системы. А так как гамильтонианы исходной
и приведённой системы связаны между
собой соотношением
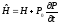
причём управление
в
не входит, то условие максимума сохраняется
и для гамильтониана исходной системы
2. Выведем условие
трансверсальности для исходной системы.
Есть условие трансверсальности для
приведённой системы
Из него необходимо вывести условие трансверсальности для исходной системы.
Воспользовавшись
:
Если рассматривается двухточечная задача, то есть область цели — точка, то условие трансверсальности определяется только терминальной составляющей
Так как обычно
полагают равным -1, условие трансверсальности
принимает следующую форму:
3. Поведение гамильтониана вдоль оптимальной траектории.
У нас есть выражение для гамильтониана
системы вдоль оптимальной траектории.
Учитывая, что гамильтониан исходной и
приведённой системы связан между собой
следующим образом:
можем получить выражение для гамильтониана исходной системы.
Когда не задано,
Когда задано,
Замечание:
Если рассматривается задача Майера, в которой функционал состоит из одной терминальной составляющей, то гамильтониан и функция Гамильтона совпадают.
Поэтому все выражения для гамильтониана будут справедливы и для функции Гамильтона. Других различий между задачей Майера и только что рассмотренной задачей нет.
Сформулируем общий принцип максимума.
Пусть дана динамическая система, которая
описывается дифференциальным уравнением
вида
Задана область начальных и конечных состояний и и допустимы х управлений U.
Если
— оптимальный процесс, в смысле минимума
функционала
(+)
то найдётся
и постоянная
,
относительно которых оптимальная
траектория определяется решением
следующей системы дифференциальных
уравнений
где
H
— гамильтониан системы, имеющий вид
Также выполняются следующие условия:
1. Условие максимума
2. Условия
трансверсальности
3. Поведение
гамильтониана вдоль оптимальной
траектории определяется соотношением
если не задано,
если задано
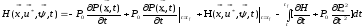
Замечание. Если ставится задача о максимуме функционала (+), принципа максимума остаётся, но постоянная полагается неотрицательной (обычно её кладут равной единице).