7. Условия трансверсальности.

В общем случае может быть задано множество начальных и множество конечных состояний системы

Необходимо найти управление , переводящее систему из области в область за мин. время.

В данном случае для оптимизации процесса необходимо, чтобы существовала непрерывная векторная функция , удовлетворяющая не только условию максимума, но и условиям трансверсальности в обоих концах траектории (t).

Условия трансверсальности состоят в том, чтобы вектор 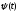был ортогонален плоскостям и , касательным к областям и соответственно в начале и в конце траектории. Будем считать, что функции ограничений и непрерывны и непрерывно дифференцируемы по x. Предположим так же, что области и ограничены, замкнуты и выпуклы.

Рассмотрим, каким условиям должна удовлетворять функция (t), если начальная точка принадлежит области начальных состояний а конечная точка является началом координат.

Т.к. — замкнутое множество, точка является граничной точкой этого множества: если бы она таковой не была, то потребовалось бы время на то, чтобы выйти за границу множества, а это было бы не оптимально.

Пусть — начальная точка оптимального процесса. Время движения из этой точки в конечную . Построим область достижимых состояний, соответствующих времени T .

Т.о. получается, что начальная точка является граничной точкой двух множеств: множества исходных и множества достижимых за время T состояний.

По теореме Хана-Банаха, два выпуклых и непересекающихся множества могут быть разделены одной гиперплоскостью. Если эти области имеют одну общую точку, то данная гиперплоскость является опорной к областям в этой точке.

Проведём гиперплоскость Г. Если гиперплоскость Г рассматривать как опорную к области достижимых состояний, то нормалью к этой гиперплоскости будет вектор .

Найдём связь между и нормалями к ограничениям :

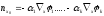, ,….,0

Для тех ограничений, которые неэффективны по теореме Куна-Таккера, . Тогда получаем

Если движение начинается из точки и заканчивается в области , то условие будет вот таким:

Совокупность этих двух условий называется условиями трансверсальности.

Замечание: если конечная область является точкой, то выбирается произвольно. Если область цели — всё фазовое пространство, то =0, так как все коэффициенты будут нулевыми (а все ограничения, соответственно, неэффективными).

8. Принцип максимума для задач управления стационарными системами с интегральным критерием качества.

Задачи управления с интегральным критерием качества:

Функция L непрерывна по своим аргументам и имеет непрерывные частные производные. . Если функция L=1, то задача оптимального быстродействия.

Условие принципа максимума для стационарных систем:

Задачи управления с интегральным критерием качества, когда функционал, область цели и уравнение состояния не зависят явно от времени.

Пусть состояние динамической системы описывается нелинейным диф. уравнением вида: .

Заданы обл. начального состояния S₀ и конечного S_f. Требуется определить условия, кот. удовл. Оптимальное управление из области допустимых и траекторию, соответствующую оптимальному управлению, удовлетворяющую граничным условиям.

.

Полагаем, что конечный момент времени t не задан.

Предположим, что L не зависит явно от времени и положительна.

1. 2.

Переходим от некоторого реального времени t к некоторому фиктивному времени . . С учетом этого исходная система диф.ур. примет вид: 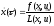. (). Тогда функционал относительно принимает вид: 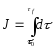(*) – свели к задаче оптимального быстродействия.

Перенесем полученные условия для задач оптимального быстродействия на более широкий класс задач. Пусть () оптимальный процесс в смысле min формулы(*), тогда он удовлетворяет принципу максимума для задачи оптимального быстродействия.

1. Существует функция , относ. кот. вып. условия: ; ;

2. Выполняется условие максимума:

3. Вдоль оптимальной траектории функция Гамильтона имеет следующий вид:

4. Выполняется условие трансверсальности.

Введем в рассмотрение функцию структуры , подставим выр-е для ф-ии Гамильтона (1)

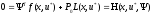(2) Эта функция наз. Гамильтонианом системы с интегральным критерием качества. Гамильтониан = 0 только вдоль оптимальной траектории. В общем случае, когда нет зависимости от времени: (3).

Введение Гамильтониана позволяет обобщить условие максимума, т.е. можно сказать, что если ()-опт. процесс, то должны выполняться следующие условия:

1. Должна существовать функция , для кот. справедливы след. соотн-ия: ;

2. Выполняется условие максимума:

3. Гамильтониан вдоль оптимальной траектории =0.

4. Выполняется условие трансверсальности.

Проверим (1а):

Перейдем от условного времени  к реальному времени t:

,- условие 1а выполняется.

Проверим (1б): , переходим от  к t: , - условие 1б выполняется.

Проверяем усл. 2: ,следовательно, ,

Рассмотрим прав.часть:  

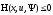
Усл. 3: Гамильтониан вдоль опт. траектории=0, это следует из его вывода и основывается на усл.2

Усл. 4: Т.к. в условие трансверсальности ни ф-ция Гамильтона ни Гамильтониан не входят, то они полностью сохр. свой вид:

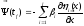
Замечание1: Мы получили условие max в предположении, что , но они выполняются и в общем случае.

Замечание2: Const P₀ обычно полагают = -1. P₀=-1