1. Структура систем управления.

Задача систем управления заключается в том, чтобы обеспечить заданные параметры развития тех или иных процессов.

Современные системы управления заключают в себя следующие компоненты:

(t) (t)

Процесс (ОУ)

Измерительная система

Управляющее устройство

u(t) x(t)

y_изм(t)

Внешняя СУ

Блок формирования эталонного процесса

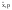
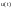
Информационный блок

u(t) – функция управления

(t) – функция возмущения (возмущение)

x(t) – состояние процесса

y_изм – функция измерения системы

(t) – функция шумов

Измерительная система – система датчиков, измеряющая параметры системы.

Управляющее устройство – система типа вход-выход, где формируются законы управления.

x^*,u^* - эталонный процесс (пара функций, определяющих динамику изменения состояния и управления процессом )

Для работы блока формирования эталонного процесса необходима информация о действительном протекании физического процесса, т.е. функции u(t) и y_изм- для информационного блока.

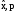– система идентификации и оценки параметров процесса.

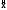– оценка состояния данного процесса

p – оценка параметров системы

Существует также внешняя СУ, ее назначение – формирование внешних команд.

Если система не содержит внешнего управления, она наз. Автономной или самодостаточной.

2. Управляемость динамических систем.

Управляемость динамических систем является их важнейшей характеристикой и определяет условия, при которых задача управления имеет решение, то есть существует одна или несколько функций входа, называемых управлениями, под действием которых динамическая система может перейти в любое наперед заданное состояние.

Будем говорить, что динамическая система управляема относительно начального состояния если существует управление из класса кусочно-непрерывных функций, которое переводит систему из начального состояния в за конечное время

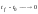
Если динамическая система управляема относительно любого начального состояния, то данная система полностью управляема.

Математические условия управляемости линейных динамических систем с постоянными параметрами.

Предположим, что начальное состояние удовлетворяет условию: 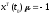, 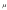некоторый n-мерный вектор. Задано конечное состояние и управление, под действием которого система переходит в это состояние.

Исходная система 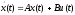и сопряженная система 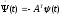, где примем .

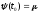Определим производную от скалярного произведения векторов состояния исходной и сопряженной систем.

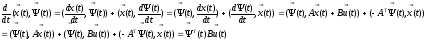
Так как 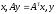, то 1 и 3 сокращаются.

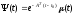Проинтегрируем это уравнение на интервале : (1), - вектор состояния сопряженной системы. - через матрицу сопряженной системы.

и ее n-1 производная:

Данную систему можно записать в матрицу вида : 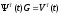(2) , G –матрица n x nm, G=[B:AB:…:A^n-1 B]. 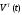- вектор 1x mn. 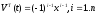Матрицу G часто называют матрицей управляемости.

Для управляемости системы необходимо и достаточно, чтобы ранг G был равен порядку системы. rang G=n

Док-во необходимости: 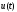- управление, под действием которого система переходит из начального состояния в состояние 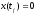, предположим, что rang G<n.

Согласно условию (1) явл. однозначн. функцией, отличной от 0 для , поэтому если rang G<n, матричное уравнение (2) будет иметь ненулевое решение относительно , 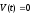. А если , 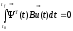  - противоречит условию 1  для управляемости исх. системы необходимо rang G=n.

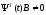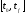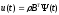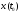Пусть rang G=n, тогда матричное уравнение 2 будет иметь ненулевое решение, если на интервале управления , это означает (3), тогда решение , u(t) – искомое управление, которое переводит систему из состояния в 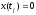. -неизвестная константа, которая определяется следующим образом: ,

Для линейной системы с одним входом матрица управляемости является квадратной матрицей размера n x n и в этом случае система будет полостью управляема, если матрица управляемости не вырождена, т.е. определитель матрицы G отличен от 0.

Свойство управляемости имеет важное значение, поскольку решение задачи синтеза оптимального управления существует только если система управляема.

Нестационарные линейные системы.

Линейная нестационарная система управляема относительно начального момента , если существует момент времени такой, что матрица является невырожденной, т.е. определитель матрицы S отличен от нуля.

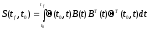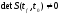, Нестационарная система полностью управляема относительно 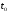, если определитель матрицы S отличен от нуля для (справедливость этого доказывается по соотношению 3).

Поскольку 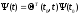( 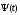- вектор сопряженной системы через переходную матрицу), то из условия (3) следует, что линейная нестационарная система управляема, если соотношение 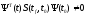. Поскольку отлично от нуля, то это означает, что определитель матрицы S должен быть отличен от нуля.