
- •Глава 1. Цифровые информационно-управляющие
- •1.2. Сигналы и варианты алгоритмов цос
- •1.3. Структура ссд
- •Глава 2. Модели сигналов,
- •2.1. Синусоидальные сигналы
- •2.1.6. Амплитудный спектр сигнала с синусоидальной
- •2.2. Комплексные сигналы. Энергетические характеристики сигналов
- •2.3. Наблюдения и модели сигналов
- •2.4. Оценивание параметров моделей сигналов
- •2.5. Модели сигналов на основе рядов Фурье. Интеграл Фурье
- •2.6. Z-Преобразование дискретных последовательностей
- •Глава 3. Предварительная обработка сигналов
- •3.1. Оценивание статистических характеристик
- •3.2. Оценивание и устранение трендов
- •3.3. Фильтрация аномальных значений в наблюдениях сигналов
- •3.4. Дискретизация непрерывных сигналов. Теорема Котельникова
2.1.6. Амплитудный спектр сигнала с синусоидальной
частотной модуляцией
2.2. Комплексные сигналы. Энергетические характеристики сигналов
Комплексные сигналы являются естественным обобщением действительных сигналов и записываются в виде
![]() ,
,
где
![]()
![]() – действительная и мнимая составляющие
комплексного сигнала
– действительная и мнимая составляющие
комплексного сигнала![]() которые определены на бесконечном
интервале
которые определены на бесконечном
интервале![]() или конечном интервале
или конечном интервале![]() времени. Комплексные сигналы могут быть
представлены в показательной форме
времени. Комплексные сигналы могут быть
представлены в показательной форме
![]()
![]()
![]()
В
качестве примера комплексного сигнала
приведём выражение для комплексной
синусоиды с параметрами A,
![]()
![]()
![]()
![]() .
.
Для
любого момента времени t
значения комплексных сигналов
![]() представляют собой комплексные числа,
над которыми можно производить все
операции комплексной арифметики.
представляют собой комплексные числа,
над которыми можно производить все
операции комплексной арифметики.
Использование комплексных сигналов доставляет определённые математические удобства; в том числе основные соотношения ЦОС записываются в комплексной форме с целью обеспечения компактности формул. Многие распространённые программы вычислений, используемые для задач ЦОС, работают с комплексными входными и выходными данными.
Энергия
E
комплексного сигнала
![]() по определению, записывается в виде
интеграла
по определению, записывается в виде
интеграла


где
звёздочка наверху
![]() является знаком комплексного сопряжения.
Данное определение энергии сформулировано
в соответствии с аналогией из электротехники
– величиной энергии, выделяемой на
активном сопротивленииR
при действии
комплексного тока
является знаком комплексного сопряжения.
Данное определение энергии сформулировано
в соответствии с аналогией из электротехники
– величиной энергии, выделяемой на
активном сопротивленииR
при действии
комплексного тока
![]()

Очевидно,
что сигналы
![]() которые
фигурируют в ЦОС, должны обладать
конечной энергией
которые
фигурируют в ЦОС, должны обладать
конечной энергией

Однако необходимо иметь в виду, что не все сигналы, фигурирующие в ЦОС, обладают конечной энергией; например, у периодических сигналов, очевидно, энергия бесконечна.
Средняя
мощность
![]() сигнала
сигнала![]() определяется
энергией, отнесённой к заданному
интервалу времени
определяется
энергией, отнесённой к заданному
интервалу времени
![]()

Мгновенная
мощность сигнала
![]() в момент времени
в момент времени![]() определяется как предел
определяется как предел
![]()

![]()
Средняя мощность действительного гармонического сигнала, определённого в разд. 2.1
![]()
на
интервале времени, который соответствует
периоду
![]() не зависит от начального момента времениt,
частоты
не зависит от начального момента времениt,
частоты
![]() и начальной фазы,
поскольку на таком интервале времени
укладывается в точности одно колебание
рассматриваемого гармонического
сигнала. В самом деле, величина средней
мощности гармонического сигнала может
быть вычислена с помощью следующего
интеграла
и начальной фазы,
поскольку на таком интервале времени
укладывается в точности одно колебание
рассматриваемого гармонического
сигнала. В самом деле, величина средней
мощности гармонического сигнала может
быть вычислена с помощью следующего
интеграла
 Средняя
мощность действительного
полигармонического сигнала
Средняя
мощность действительного
полигармонического сигнала
![]()
![]()
на
отрезке времени
![]() должна представиться в виде интеграла
должна представиться в виде интеграла

который
вычисляется достаточно сложным образом
для произвольных значений t,
![]() и частот
и частот![]() Рассмотрим частный случай, когда частоты
сигнала являются упорядоченными
Рассмотрим частный случай, когда частоты
сигнала являются упорядоченными![]() и
и![]() кратны наименьшей частоте
кратны наименьшей частоте![]() Последнее означает, что существуют
целые числа
Последнее означает, что существуют
целые числа![]()
![]()
![]() и
и![]() которые обеспечивают равенства
которые обеспечивают равенства![]()
![]() являющееся условием кратности для
частот. Рассмотрим интервал интегрирования
являющееся условием кратности для
частот. Рассмотрим интервал интегрирования![]() равный наибольшему периоду для частот
равный наибольшему периоду для частот![]()
![]() составляющих полигармонического
сигнала. Кратность указанных частот
означает, что все составляющие укладываются
в точности целое число раз на времени
составляющих полигармонического
сигнала. Кратность указанных частот
означает, что все составляющие укладываются
в точности целое число раз на времени![]() и выполняются следующие равенства
и выполняются следующие равенства
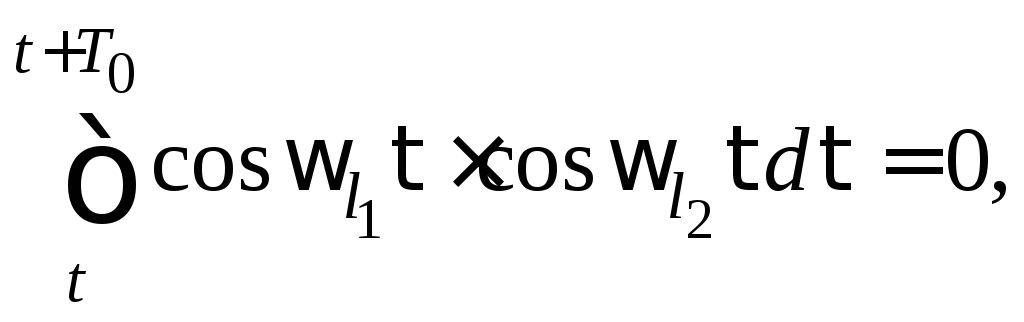

![]()

Благодаря
указанным равенствам для полигармонических
составляющих следует, что средняя
мощность P
такого полигармонического сигнала
равняется сумме средних мощностей
![]() гармонических составляющих
гармонических составляющих
![]()
![]()
![]()
Для
полигармонических сигналов с кратными
частотами возможно наглядное
представление дискретного спектра
мощности сигнала в виде набора
дискретных значений отдельных мощностей
![]() соответствующих частотам
составляющих
соответствующих частотам
составляющих![]() где
где![]() (рис. 2.2.1).
(рис. 2.2.1).

Рис. 2.2.1. Дискретный спектр мощности
