
Магнитная труктура поверхностей и тонких пленок
.pdfПрофиль намагниченности в приповерхностной области
ферромагнетика и в тонких пленках
Введение
Определение равновесной спиновой конфигурации вблизи поверхностей и границ раздела сред является ключевым в понимании природы магнитного поведения кристаллов с поверхностью, тонких пленок и многослойных систем, состоящих из различных пленок.
Для поверхностей характерно появление отличной от объемной энергии анизотропии,
возникающей из-за различия в симметрии окружения атомов на поверхности и в объеме
(анизотропия Нееля). Поверхностная анизотропия может способствовать появлению как перпендикулярной к плоскости поверхности намагниченности, так и параллельной к ней
[1]. Этот терм в термодинамическом потенциале магнитной системы конкурирует как с магнитно-дипольной энергией, так и с объемной магнитокристаллической анизотропией,
которая также может способствовать появлению, как перпендикулярной намагниченности, так и намагниченности, лежащей в плоскости поверхности. Подобного рода эффекты приводят к тому, что вблизи поверхности может образоваться скошенная магнитная структура (СМС) типа доменной стенки, в которой ориентация намагниченности атомного слоя меняется с номером этого слоя. При уходе вглубь кристалла происходит переход к объемной ориентации моментов атомных слоев [2,3].
Цель настоящей лекции состоит в том, чтобы построить диаграммы магнитных состояний полупространственного ферромагнетика и тонких пленок в координатах (KS, KB). KS и KB – константы поверхностной и объемной анизотропии соответственно. Эта проблема рассматривается здесь в рамках простейшего приближения, часто используемого при трактовке магнитных свойств: модель Гейзенберга с классическими моментами и изотропным обменным взаимодействием. Индекс n = 1 соответствует поверхностному атомному слою с константой анизотропии второго порядка KS.
Остальным слоям, обозначаемым индексами n = 2, 3,… , приписывается константа анизотропии также второго порядка KB, отличающаяся от KS, и не зависящая от индекса слоя n. Анизотропия внутри плоскости каждого из атомных слоев не учитывается.
Обменное взаимодействие между слоями полагается ферромагнитным Jn,n+1 J > 0. В
такой формулировке проблема сводится к выяснению основного магнитного состояния одномерной цепочки, энергия которой может быть записана следующим образом
N |
N |
|
E J cos( n |
n 1 ) KS sin2 1 KB sin2 n , |
(1) |
n 1 |
n 2 |
|
где n – угол между вектором момента n-го слоя и плоскостью поверхности, Рис.1.
1

Рис. 1. Схематическое изображение скошенной магнитной структуры (СМС) в приповерхностной области полубесконечного кристалла при учете дискретности атомных слоев. В объеме кристалла анизотропия типа легкая плоскость, в поверхностном атомном слое анизотропия типа легкая ось, перпендикулярная плоскости поверхности.
§1. Фазовая диаграмма магнитных состояний полубесконечного ферромагнетика в
случае поверхностной анизотропия типа легкая ось и объемной анизотропии типа
легкая плоскость.
Возникновение СМС в полубесконечном ферромагнетике с анизотропией в объемных слоях типа легкая плоскость связано с малым отклонением моментов приповерхностных атомных слоев от ориентации в плоскости пленки. При этом СМС возникает тогда, когда оно становится энергетически более выгодным по сравнению с коллинеарным упорядочением всех моментов, ориентированных параллельно поверхности. Везде ниже оно называется параллельным состоянием. В этом случае вывод критерия появления СМС подразумевает, что в (1) каждый из углов n должен быть
отклонен от нулевого значения, а возникающее при этом изменение энергии должно быть
проанализировано. Для малых изменений углов n |
выражение для энергии в (1) может |
||||||
быть записано в виде ряда по углам n |
с точностью до членов второго порядка в виде |
||||||
квадратичной формы, которая в компактной записи имеет вид |
|
||||||
|
|
|
|
, , |
|
|
|
E E T A |
( , |
2 |
N |
) . |
(2) |
||
0 |
|
1 |
|
|
|
||
Здесь E0 – часть энергии, не зависящая от углов n , а A – квадратная трехдиагональная
|
|
|
|
|
матрица размерности (N x N) с действительными элементами. N собственных векторов an |
||||
этой матрицы ортогональны друг другу и образуют базис в |
N-мерном пространстве. |
|||
|
|
|
|
|
Раскладывая вектор по базису из векторов an , |
|
|||
|
|
|
|
|
c1a1 |
c2a2 |
cN aN |
(3) |
|
выражение для энергии (2) можно переписать следующим образом
2
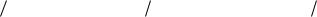
N |
|
E Eo n | cn |2 . |
(4) |
n |
|
Здесь n – n-ое собственное значение матрицы |
A. Минимизация энергии (4) |
подразумевает варьирование коэффициентов cn, которые в соответствии с (3) определяют профиль СМС. Таким образом, для заданных значений параметров модели KS, KB, J, N
минимальная энергия соответствует конкретному виду профиля СМС в приповерхностной
области магнетика. Из |
формулы (4) |
видно, что |
если все |
собственные |
значения |
n |
|
|
|
|
|
|
|
положительны, то энергия минимальна, только если все |cn|2=0. Это отвечает случаю 0 |
||||||
, т.е. коллинеарному |
параллельному |
состоянию. |
Однако, |
если хотя |
бы одно |
из |
собственных значений n становится отрицательным, условие 0 уже не соответствует энергетическому минимуму. В этом случае параллельное состояние не является выгодной магнитной конфигурацией. Таким образом, критерий появления СМС состоит в том,
чтобы минимальное из собственных значений матрицы А оказалось меньше нуля.
Для того, чтобы выразить этот критерий на языке параметров модели, следует найти это минимальное собственное значение min и решить неравенство min < 0.
Уравнение на собственные значения матрица A имеет вид
|
|
|
|
/ 2 |
1/ 2 |
0 |
0 |
|
|
0 |
0 |
|
|
|
||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/ 2 |
|
|
|
1/ 2 |
0 |
|
|
|
|
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1/ 2 |
|
|
1/ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
det | A I | J N det |
|
|
0 |
|
0 |
1/ 2 |
|
|
|
0 |
0 |
|
0 |
(5) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1/ 2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
1/ 2 |
|
|
1/ 2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
0 |
0 |
1/ 2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где 1 KB |
J , |
J , |
1 2(KS KB ) |
J , |
– |
поверхностное |
||||||||||||
возмущение, которое возникает как из-за отсутствия атомного слоя над поверхностью, так
и из-за отличия поверхностной константы анизотропии KS от объемной KB. Поскольку в этом и следующем параграфах рассматривается полубесконечный кристалл (N ), на другой стороне пленки поверхностным возмущением можно пренебречь, поэтому в нижнем правом углу матрицы (5) положено равным нулю. Тогда (5) принимает вид
d |
N |
d |
N 1 |
0 . |
(6) |
|
2 |
|
|
||
|
|
|
|
|
Здесь dN – определитель матрицы размерности (N x N), аналогичной (5), в которой все диагональные матричные элементы положены одинаковыми и равными .
3

Вид формулы для определителя dN |
зависит от значения параметра |
[7]. |
|||||
Поскольку выражение для содержит обезразмеренное собственное значение = |
/J, |
||||||
|
|
|
|
|
|
|
|
форма уравнения (6) зависит от того в каком интервале оно ищется. |
|
||||||
(I) | | 1. Это |
условие означает, что собственное значение принадлежит «зоне», |
т.е. |
|||||
1 1, |
или эквивалентно |
|
|
|
|
||
|
|
KB |
1 1 |
KB |
2 . |
(7.1) |
|
|
|
|
|
||||
|
|
J |
|
J |
|
||
Поскольку в этом параграфе рассматривается объемная анизотропия, способствующая ориентации моментов в плоскости, то константа KB положительна. Таким образом, ни одно из собственных значений, принадлежащих «зоне», никогда не пересекает ноль.
(II) 1. Это неравенство может быть переписано в виде
|
|
|
2 |
KB |
2 1 . |
(7.2) |
||
|
|
|
|
|||||
|
|
|
|
J |
|
|||
Следовательно, аналогично случаю (I), и здесь собственное значение не пересекает ноль. |
||||||||
(III) |
|
1 |
. Это неравенство может быть переписано в виде |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
KB |
. |
(7.3) |
||
|
|
|
|
|||||
|
|
|
|
|
|
J |
|
|
Таким образом, только в случае (III) оказывается возможным получить отрицательное |
||||||||
собственное значение . В этом случае определитель dN |
имеет следующий вид: |
|||||||
d |
|
|
sinh (N 1) |
, |
cosh |
|
, |
0 . |
|
N |
2N sinh |
|
|||||||
|
|
|
|
|
|
Подстановка (8) в (6) приводит к следующему уравнению на min :
sinh (N 1) . sinh N
Для полубесконечного кристалла (N ), уравнение (9) принимает вид
lim N sinh (N 1) exp( ) . sinh N
(8)
(9)
(10)
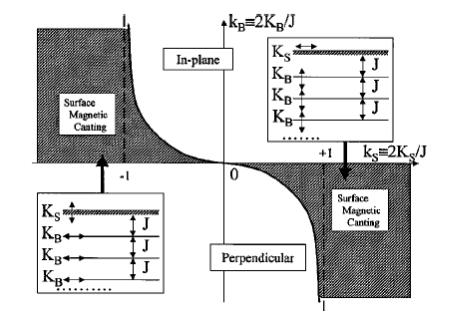
Так как > 0, то уравнение (10) имеет решение только при < – 1. На языке параметров модели это означает, что константа KS должна быть меньше KB. В соответствии со сказанным выше KS < 0 KB > 0, и, следовательно, это требование выполняется. Из уравнения (10) можно получить выражение для обезразмеренного собственного значения
, которое имеет следующий вид
|
1 |
|
1 |
|
|
|
|
|
|
. |
(11) |
|
|
||||
|
2 |
|
|
|
4
Неравенство < 0, означающее критерий неустойчивости параллельного состояния и возникновения СМС, может быть переписано на языке параметров модели kS и kB:
kS |
1 |
|
1 |
|
. |
(12) |
|
|
|
||||
kB |
(kS |
|
||||
|
|
1) |
|
|||
При –1 < kS < 0 неравенство (12) удовлетворяется для значений kB, меньших некоторого порогового значения, определяемого формулой
kB kS |
1 |
|
1 |
|
. |
(13) |
|
|
|
|
|||||
kS |
1 |
||||||
|
|
|
|
||||
При kS < –1 неравенство (12) удовлетворяется для любых положительных значений kB.
Последнее указывает на то, что при kS < –1 СМС реализуется в приповерхностной области независимо от того насколько велика константа объемной анизотропии kB. Область,
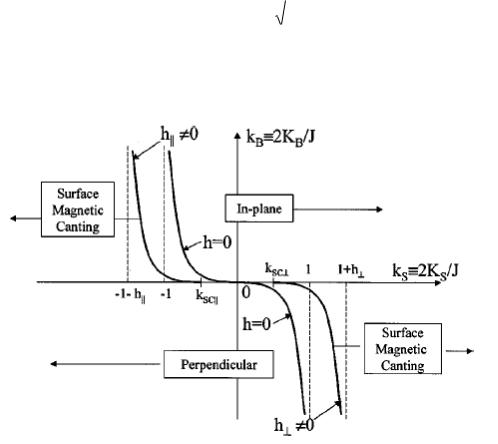
соответствующая СМС в полубесконечном кристалле с объемной анизотропией типа легкая плоскость (kB >0) и поверхностной анизотропией типа легкая ось, kS < 0, находится в левом верхнем углу на фазовой диаграмме (kS, kB), представленной на Рис.2.
Рис. 2. Фазовая диаграмма магнитных состояний полубесконечного ферромагнитного кристалла в координатах приведенных констант поверхностной kS и объемной kB анизотропии. СМС – область,
отвечающая скошенной магнитной структуре, заштрихована. Линия, ограничивающая область СМС в левом верхнем углу диаграммы, определяется формулой (13). Линия, ограничивающая область СМС в правом нижнем углу диаграммы, определяется формулой (15).
§ 2. Фазовая диаграмма магнитных состояний полубесконечного ферромагнетика в случае поверхностной анизотропия типа легкая плоскость и объемной анизотропии типа легкая ось.
5
Обобщение полученного результата на случай поверхностной анизотропии,
способствующей ориентации момента в плоскости пленки, и объемной анизотропии,
приводящей к перпендикулярной ориентации момента объемных слоев (kS < 0, kB < 0) не вызывает особых затруднений. В этом случае следует переопределить понятие СМС,
поскольку теперь СМС соответствует отклонению моментов атомов приповерхностных слоев уже от нормали к поверхности, а не от плоскости пленки. В соответствии с этим новым определением теперь более удобно отсчитывать углы ориентации моментов от нормали к поверхности. Таким образом, мы вводим углы n = /2- n и раскладываем энергию (1) до второго порядка по каждому из n. В этом случае уравнение на приведенное собственное значение (11) остается справедливым. Отличие состоит в том,
что теперь поверхностное возмущение определяется формулой 1 2(KS KB ) J . В
J . В
результате в терминах kS и kB критерий неустойчивости перпендикулярного состояния и появления СМС в приповерхностной области ферромагнетика приобретает вид
1 |
|
kS |
1. |
(14) |
|
|
|||
kB (kS |
|
|||
1) |
|
|
||
Анализ этого неравенства для kB < 0 и kS > 0 приводит к следующему. При 0 < kS < 1
неравенство (14) удовлетворяется при отрицательных величинах kB, меньших некоторого критического значения, определяемого формулой
kB kS |
1 |
|
1 |
|
. |
(15) |
|
|
|
|
|||||
kS |
1 |
||||||
|
|
|
|
||||
При ks > 1 неравенство (14) удовлетворяется для любых сколь угодно больших значений
|kB|. Область, соответствующая СМС в ферромагнетике с объемной анизотропией легкая ось поверхностной анизотропией легкая плоскость показана в правом нижнем углу фазовой диаграммы в координатах (kS, kB), представленной на Рис 2.
Теперь дадим физическую трактовку полученной фазовой диаграммы. Важной особенностью этой диаграммы является то, что в обеих частях присутствуют области, в
которых СМС реализуется при любых значениях константы объемной магнитной анизотропии, если выполняется условие | kS |>1. Существование такой области в левой верхней части диаграммы, ограниченной асимптотой kS = –1, проще всего понять в предельном случае kB . В этом случае каждый из объемных моментов (n = 2, 3, …)
ориентирован в плоскости пленки. Как следствие, проблема сводится к однослойному приближению и может быть легко проанализирована аналитически. Выражение для энергии (1) тогда имеет следующий вид
E1 J cos 1 KS sin2 1 .
6

Минимизация E1 по углу ориентации 1 дает следующие результаты
|
|
|
|
J |
|
|
|
|
J |
|
sin 1 0 |
|
1 0 и cos 1C |
|
|
|
1C |
|
|
|
|
|
|
|||||||||
2KS |
arccos |
|
. |
|||||||
|
|
|
|
|
|
|
|
2KS |
||
Разница в энергиях, отвечающих этим решениям, определяется формулой
E1 E1 ( 1 1C ) E1 ( 1 0) (J 2KS )2 0 . 4KS
Поскольку здесь анализируется случай перпендикулярной поверхностной анизотропии,
рассмотренный в разделе 1, константа поверхностной анизотропии KS отрицательна.
Поэтому разница энергий E1 также отрицательна, и СМС всегда энергетически выгодно.
Однако отклонение поверхностного момента определяется формулой cos 1 = –1/kS. Таким образом, состояние СМС может реализоваться только для тех значений kS, которые соответствуют условию cos 1 < 1, то есть kS < –1. Также в этом частном случае может быть получено выражение для восприимчивости в перпендикулярном магнитном поле
(kS |
1) |
|
1 |
|
, |
|
|
|
|
|
|||||
2(kS |
|
|
|||||
|
|
|
|
1) |
(16) |
||
|
|
|
|
|
1 |
||
(kS |
1) |
|
|
|
. |
||
|
|
|
|
||||
|
2(kS |
1)kS (1 kS ) |
|||||
|
|
|
|
|
|||
Как следует из этих формул, в окрестности перехода между СМС и однородным состоянием с моментом, ориентированным в плоскости пленки, оба выражения (kS<–1) and (kS>–1) расходятся. Кроме этого они удовлетворяют соотношению (kS>–1) = 2 (kS<–1), демонстрируя тем самым, что этот переход второго рода. Это утверждение относится ко всем границам на фазовой диаграмме, представленной на Рис. 2.
§ 3. Влияние внешнего магнитного поля на фазовую диаграмму магнитных состояний полубесконечного ферромагнетика.
После того, как было показано, что уравнения всех линий на фазовой диаграмме могут быть получены в квадратурах (12-15), теперь можно рассмотреть эффект влияния внешнего магнитного поля h 0 на границы на фазовой диаграмме. В случае, когда kS < 0, kB > 0, учет внешнего магнитного поля, ориентированного в плоскости пленки, h||,
приводит к дополнительному слагаемому в выражении для энергии E.
N
E J cos( n
n 1
N |
N |
|
n 1 ) KS sin2 1 KB sin2 n |
h|| cos n . |
(17) |
n 2 |
n 1 |
|
В этом случае процедура нахождения собственного значения оказывается той же самой.
Это связано с тем, что матрица A имеет тот же вид потому, что поверхностное
7
возмущение то же самое. Аналогично, уравнение (11) на собственные значения остается справедливым. Однако параметр теперь определяется как = 1 + ks/2 + h||/2. Как следствие, критерий нестабильности параллельного состояния имеет иную форму:
kS 1 h|| |
|
|
1 |
|
. |
(18) |
|
|
|
||||
kB |
(kS |
|
||||
|
|
1) |
|
|||
Анализ этой формулы показывает, что включение поля h|| |
приводит к увеличению области |
|||||
на фазовой диаграмме (kS, kB), которой соответствует ориентация момента в плоскости.
Эволюция движения границ, разделяющих однородное состояние и состояние СМС,
состоит в следующем. Во-первых, асимптота kS= –1 сдвигается влево, поскольку теперь ее положение определяется формулой kS= –1–h||. Во-вторых, учет внешнего магнитного поля,
ориентированного в плоскости пленки, приводит к наличию конечного интервала значений kS , в котором СМС не может реализоваться при kB = 0. Таким образом, в этом случае состояние СМС оказывается подавленным и появляется, только если kS меньше некоторого критического значения, определяемого формулой
|
|
|
|
|
h |
h2 |
4h |
|
|
|
k |
|
k |
|
|
|| |
|| |
|| |
. |
(19.1) |
|
S |
SC|| |
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Граница между областью, отвечающей СМС, и областью, отвечающей однородному состоянию, для h 0 показана на фазовой диаграмме, представленной на Рис. 3.
Рис. 3. Эволюция границы области СМС на фазовой диаграмме в координатах kS и kB при включении внешнего магнитного поля h||, параллельного плоскости пленки, определяется (19.1) и показана в левой верхней части диаграммы. Эволюция границы области СМС при включении внешнего магнитного поля h ,
перпендикулярного плоскости пленки, определяется (19.2) и показана в правой нижней части диаграммы.
8
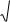
Учет внешнего магнитного поля h , перпендикулярного плоскости пленки для kS > 0, kB <
0, приводит к аналогичным изменениям в нижнем правом углу фазовой диаграммы, как показано на том же рисунке. Выражение для kSC определяется формулой
|
|
|
|
|
h |
h2 |
4h |
|
|
|
k |
|
k |
|
|
|
|
|
. |
(19.2) |
|
S |
SC |
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
§ 4. Магнитное состояние однородных в плоскости тонких пленок.
При учете конечности числа атомных N слоев в пленке, во-первых, возникает необходимость в учете поверхностного возмущения также и на противоположной стороне пленки в уравнении (5) . Во-вторых, необходимо решить получающееся уравнение без упрощающего предположения N . Решение уравнения (5) для конечного числа атомных слоев представляет особый интерес для тонкопленочного магнетизма. Однако необходимость учета поверхностного возмущения на обеих сторонах пленки вносит дополнительные усложнения. Ради простоты мы здесь рассмотрим два крайних случая:
(A) тонкая пленка нанесена на магнитную подложку, имеющую очень малую глубину проникновения СМС, то есть подложка сильномагнитная и (В) тонкая пленка нанесена на немагнитную подложку.
(A): В этом предельном случае уравнение (9) остается справедливым, поскольку поверхностное возмущение на другой стороне пленки уже учтено, то есть положено n = 0
для n > N (см. Рис. 1). Тогда правая сторона (9) может быть записана в виде
|
sinh (N 1) |
exp( ) exp( ) exp( ) |
exp( 2 N ) |
|
|
sinh N |
1 exp( 2 N ) |
||||
|
|
(20) |
exp( ) exp( ) exp( ) exp( 2 N ).
Из этой формулы следует, что возникающая поправка к нашему предыдущему результату,
формула (10), полученному в предельном случае N уменьшается экспоненциально с толщиной пленки. Более существенно, что эта поправка положительна в интервале 0 < < + . Это приводит к следующим последствиям. Уравнение (19) удовлетворяется при меньших значениях параметра для данного значения параметра – . Имея ввиду соотношение = – cosh( ) (см. определение параметров , , и в (5) и (8)), можно заключить, что учет конечности числа атомных слоев приводит к уменьшению параметра
, что в свою очередь ведет к увеличению минимального собственного значения . Как следствие, пересекает ноль позже, поскольку для того, чтобы удовлетворить требованию
= 0, нужно большее значение константы поверхностной анизотропии по сравнению со случаем полубесконечного кристалла. Таким образом, возникновение СМС в тонкой
9
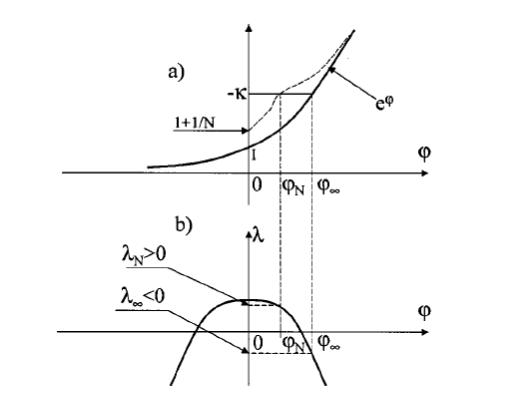
пленке, нанесенной на сильномагнитную подложку, подавлено. Эта ситуация
иллюстрируется на Рис. 4.
Рис. 4. (a) Графическое решение уравнения (10) на параметр , отвечающий минимальному собственному значению матрицы A (5) для полубесконечного ферромагнетика (непрерывная линия). (а). Графическое решение уравнения (20) на параметр для пленки из N слоев, нанесенной на подложку из жесткого магнетика (штриховая линия). (b) Графическая иллюстрация случая, когда критерий СМС для полубесконечного ферромагнетика выполнен ( <0), а для пленки из N слоев с теми же величинами kS и kB –
нет (0<N).
Ниже приведены решения для нескольких конкретных значений числа атомных слоев в пленке N.
N = 1. В этом случае проблема сводится к однослойному приближению,
рассмотренному в разделе 2. СМС должна трактоваться как отклонение только лишь поверхностного момента от ориентации в плоскости пленки. Оно имеет место при kS < –1,
и, таким образом, на фазовой диаграмме область СМС совпадает с областью, в которой поверхность находится в состоянии СМС независимо от значения константы объемной анизотропии на фазовой диаграмме на Рис. 2. Для –1< kS < 0 момент однослойной пленки всегда ориентирован в плоскости пленки.
N = 2. В этом случае область СМС больше, чем в случае N = 1. Если kS < –1, то аналогично случаю N = 1 СМС имеет место независимо от величины kB > 0, тогда как при kS > – 1 СМС имеет место, только если kB удовлетворяет условию
10
