Глава 5. Матрицы и определители

В этой главе приводятся краткие справочные сведения из разделов, относящихся к курсу линейной алгебры.

5.1. Определители и их свойства

5.1.1. Подстановки

Рассмотрим набор из первых натуральных чисел.

Набор этих чисел, расположенных в каком-либо порядке, называется перестановкой. Число перестановок .

Переход от одной перестановки к другой переменой мест двух чисел называется транспозицией. Все перестановок можно расположить в таком порядке, что каждая последующая перестановка будет отличаться от предыдущей одной транспозицией. Числаобразуют в данной перестановке инверсию, еслиистоит раньше

.

Если число инверсий в перестановке четно, но она называется четной.

Всякая транспозиция меняет четность перестановки. Перемена четности перестановки при транспозиции рядом стоящих чисел очевидно. Для удаленных чисел доказательство проводится по индукции. Перестановку удобно определять, как отображение

.

При перестановке столбцов это отображение не меняется. Таким образом, любую подстановку можно задать отображением

.

Подстановка будет четна, если четна нижняя подстановка.

5.1.2. Определитель

Рассмотрим квадратную матрицу

и всевозможные произведения по элементов, взятых по одному разу из каждой строки и каждого столбца

, (1)

Индексы образуют некоторую перестановку изчисел. Число таких произведений.

Определение. Определитель матрицы обозначается и определяется, как сумма всевозможных произведений вида (1), каждый из которых берется со знаком +, если подстановка

четна, и со знаком минус в противном случае.

Определение. Операция транспонирования определяется, как переход к матрице, в которой элементы меняются местами. Операция транспонирования обозначается звездочкой .

Slide_5_1 «Транспонирование»

Свойства определителей.

Свойство 1. Определитель не меняется при трансронировании.

Следствие. Всякое свойство, касающееся строк, будет справедливо и для столбцов.

Таким образом, все свойства 2-8 будут справедливы и для столбцов.

Свойство 2. Если одна из строк состоит из нулей, то определитель равен нулю.

Свойство 3. При перестановке двух строк определитель меняет знак.

Свойство 4. Определитель, содержащий две одинаковые строки равен нулю.

Свойство 5. Если все элементы строки умножить на некоторое число, то определитель умножается на это число.

Свойство 6. Определитель, содержащий две пропорциональные строки равен нулю.

Свойство 7. Если одна из строк является линейной комбинацией других строк, то определитель равен нулю.

Свойство 8. Определитель не изменится, если к одной строке прибавить другую строку, умноженную на некоторое число.

5.1.3. Миноры и их дополнения

Минором порядка (обозначается) называется определитель матрицы-го порядка, стоящей на пересечении строки столбцовисходной матрицы. Дополнительный миноропределяется, как определитель матрицы составленный из строк с номерам, отличными оти из столбцов с номерами, отличными от. Алгебраическое дополнениеопределяется, как

.

Теорема (О разложении определителя по строке).

Определитель равен сумме элементов какой-либо строки, умноженных на алгебраические дополнения к этим элементам.

.

5.2. Прямоугольные матрицы

Рассмотрим прямоугольную матрицу

,

имеющую строк истолбцов. Говорят, что матрица имеет тип.

5.2.1. Операции над матрицами

1) Операция умножения матрицы на число определяется по правилу

.

3. Операция сложения двух однотипных матриц определяется по правилу

.

4. Операция умножения двух матриц (типы матриц должны быть согласованы, как указано ниже) определяется по правилу

Из свойств операции умножения матриц отметим свойство умножения определителей

5.3. Обратные матрицы

Квадратная матрица называется вырожденной, если ее определитель равен нулю, в противном случае матрица называется невырожденной.

Символ Кронекера определяется по правилу:

, если и, если,

Матрица называется единичной, если

Для единичной матрицы справедливо свойство

для любой матрицы того же типа .

Матрица назыается обратной к матрице и обозначается , если она удовлетворяет свойству

Матрица назыается обратимой, если для нее существует обратная матрица.

Теорема. Матрица обратима тогда и только тогда, когда она невырождена.

Определение. Матрица из алгебраических дополнений, поставленных на места соответствующих элементов называется присоединенной матрицей

- присоединенная матрица к .

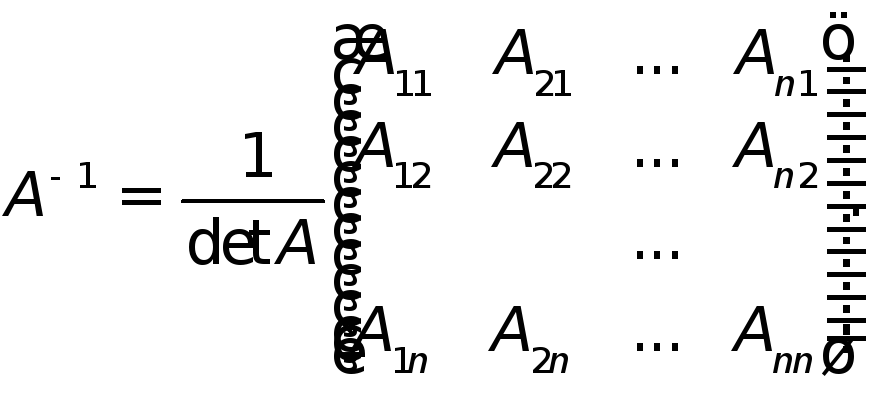
Правило построения обратной матрицы к матрице

.

1. Состаляется присоединенная матрица

2. Присоединенная матрица транспонируется

3. Полученная матрица делится на

5.4. Системы линейных уравнений

5.4.1. Запись системы линейных уравнений в матричной форме

Рассмотрим систему линейных уравнений

. (1)

Решением системы (1) называется набор чисел , при подстановке которых в уравнения системы (1) они превращаются в верные равенства.

Система, имеющая хотя бы одно решение называется совместной, в противном случае система называется несовместной. Если ввести матрицы

,

то система (1) согласно правилам умножения матриц запишется в виде

.

В случае, когда число уравнений системы совпадает с числом неизвестных и матрица коэффициентов системы невырождена (), решение этой системы можно записать в матричной форме . Действительно, домножим равенство слева на обратную к матрицу. Получим

.

5.4.2. Правило Крамера

Рассмотрим тот же случай, что и в предыдущем пункте: число уравнений системы совпадает с числом неизвестных и матрица коэффициентов системы невырождена, . Правило Крамера позволяет находить решение такой системы по формуле

.

Другими словами, - ое неизвестное системы уравнений равно дроби, знаменателем которой является определитель матрицы коэффициентов системы, а числитель равен определителю матрицы коэффициентов системы, в которой-й столбец заменен на столбец свободных членов системы.

78