
- •Статика
- •1. Введение в статику
- •1.1. Основные понятия статики
- •1.2. Аксиомы статики
- •1.3. Основные виды связей и их реакции
- •1. Теорема о переносе силы вдоль линии действия.
- •2. Теорема о трех силах.
- •2. Свойства систем сил, приложенных к твердому телу
- •2.1. Система сходящихся сил
- •2.2. Проецирование силы на оси координат
- •2.3. Алгебраический момент силы относительно точки
- •2.4. Векторный момент силы относительно точки
- •2.5. Момент силы относительно оси
- •2.6. Связь момента силы относительно оси
- •2.7. Пара сил. Алгебраический момент пары сил
- •2.8. Теорема об эквивалентности двух пар сил,
- •2.9. Теорема о переносе пары сил в параллельную плоскость
- •2.10. Векторный момент пары сил
- •2.11. Теорема о сумме моментов сил пары
- •2.12. Сложение пар сил
- •2.13. Условия равновесия системы пар сил
- •2.14. Приведение силы к заданному центру
- •1. Теорема о параллельном переносе силы.
- •2. Теорема Пуансо (основная теорема статики).
- •2.15. Приведение плоской системы сил
- •2.16. Условия равновесия системы сил
- •1. Пространственная система параллельных сил
- •2. Плоская произвольная система сил
- •3. Плоская система параллельных сил
- •2.17. Теорема Вариньона (о моменте равнодействующей)
- •2.18. Плоская система сил
- •2.19. Статически определимые и статически неопределимые задачи
- •2.20. Распределенные силы
- •2.21. Реакция жесткой заделки
- •3. Трение
- •3.1. Трение скольжения
- •3.2. Законы Кулона
- •3.3. Угол и конус трения
- •3.4. Равновесие тела на шероховатой поверхности
- •3.5. Трение качение
- •4.Пространственная система сил
- •4.1. Изменение главного момента при перемене центра приведения
- •4.2. Инварианты системы сил
- •4.3. Частные случаи приведения пространственной системы сил
- •4.4. Центр параллельных сил
- •4.5. Центр тяжести и методы его нахождения
- •4.6. Определение центров тяжести простейших однородных тел
- •1. Кинематика точки
- •1.1. Траектория движения, скорость и ускорение точки
- •1.2. Способы изучения движения точки
- •1. Векторный способ.
- •2. Координатный способ.
- •3. Естественный способ.
- •1.3. Естественный трехгранник
- •1.4. Ускорение точки при естественном способе задания движения.
- •2. Простейшие движения твердого тела
- •2.1. Степени свободы твердого тела
- •2.2. Теорема о проекциях скоростей точек твердого тела
- •2.3. Поступательное движение твердого тела
- •2.4. Вращение твердого тела вокруг неподвижной оси
- •2.5. Скорость и ускорение точки тела,
- •3. Плоское движение твердого тела
- •1. Разложение плоского движения твердого тела на поступательное и вращательное. Уравнения плоского движения твердого тела
- •3.2. Скорости точек тела при плоском движении.
- •3.3. Ускорение точек тела при плоском движении.
- •3.4. Теорема о конечном перемещении плоской фигуры.
- •4. Сложное движение точки
- •4.1. Основные понятия сложного движения точки
- •4.2. Абсолютная и относительная производные от вектора.
- •4.3. Сложение скоростей
- •4.4. Сложение ускорений
- •4.5. Ускорение Кориолиса
- •4.6. Сложное движение твердого тела
- •1. Сложение поступательных движений
- •2. Сложение вращений вокруг пересекающихся осей
- •3. Пара вращений.
- •4. Сложение вращений вокруг параллельных осей.
- •3. Закон равенства действия и противодействия.
- •4. Закон независимости действия сил.
- •1. Динамика материальной точки
- •1.1. Дифференциальные уравнения движения материальной точки
- •Центр тяжести
- •1. Сложение параллельных сил. Центр параллельных сил
- •2. Центр тяжести тел
- •1. Трение скольжения
- •2. Трение качения
- •Кинематика точки
- •1.Способы задания движения точки
- •2. Скорость точки
- •3. Ускорение точки
- •Основные виды движения твёрдого тела
- •1. Поступательное движение тела
- •2. Вращение тела вокруг неподвижной оси
- •3. Вращение тела вокруг неподвижной точки
3. Вращение тела вокруг неподвижной точки
Название такого вида движения довольно точно его определяет. Часто это движение называют сферическим движением потому, что все точки тела движутся по сферическим поверхностям.
Наглядным примером такого движения является волчок, закономерности движения которого лежат в основе гироскопических приборов.
Углы Эйлера. Уравнения вращения тела с одной неподвижной точкой.
П
Рис. 9.5.
Рис. 9.5.![]() (пси),
(пси),
![]() (тета),
(тета),![]() (фи).
(фи).
Положение тела определяется следующим
образом. Назначаются две системы
декартовых осей. Первая система –
неподвижные оси
![]() .
Начало которых берётся в неподвижной
точке
.
Начало которых берётся в неподвижной
точке![]() тела (рис. 9.5). Вторая система, оси
тела (рис. 9.5). Вторая система, оси![]() ,
связывается с телом. Поэтому положение
тела будет
,
связывается с телом. Поэтому положение
тела будет
определятся как положение этих осей относительно неподвижных.
К
Рис. 9.5.
Рис. 9.4.
Рис. 9.5.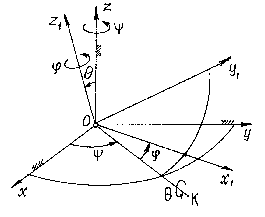
![]() вокруг оси
вокруг оси![]() .
При этом оси
.
При этом оси![]() и
и![]() отойдут от осей
отойдут от осей![]() и
и![]() в горизонтальной плоскости и ось
в горизонтальной плоскости и ось![]() займёт положение
займёт положение![]() (рис.9.5)..Затем тело
вращаем вокруг нового положения
оси
(рис.9.5)..Затем тело
вращаем вокруг нового положения
оси![]() (прямой
(прямой![]() )
на угол
)
на угол![]() .
Ось
.
Ось![]() отойдёт от оси
отойдёт от оси![]() на этот угол
на этот угол![]() ,
а ось
,
а ось![]() приподнимется над горизонтальной
плоскостью. Наконец, тело (и подвижные
оси) вращаем вокруг нового положения
оси
приподнимется над горизонтальной
плоскостью. Наконец, тело (и подвижные
оси) вращаем вокруг нового положения
оси![]() на угол
на угол![]() .
Ось
.
Ось![]() отойдёт от положения
отойдёт от положения![]() в наклонной плоскости, перпендикулярной
оси
в наклонной плоскости, перпендикулярной
оси![]() .
Это положение тела и будет соответствовать
углам Эйлера (на рисунке само тело не
показано).
.
Это положение тела и будет соответствовать
углам Эйлера (на рисунке само тело не
показано).
Линия пересечения неподвижной плоскости
![]() и подвижной
и подвижной![]() ,
прямая
,
прямая![]() ,
называетсялинией узлов. Угол
,
называетсялинией узлов. Угол![]() называетсяуглом прецессии, угол
называетсяуглом прецессии, угол![]() –углом нутации, угол
–углом нутации, угол![]() –углом собственного вращения. Эти
названия углов пришли из теории
гироскопов.
–углом собственного вращения. Эти
названия углов пришли из теории
гироскопов.
П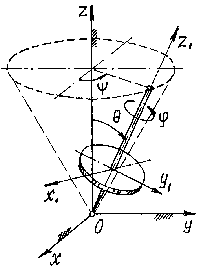
 ри
движении тела углы Эйлера изменяются
по определённым законамккккккккккккф
.
ри
движении тела углы Эйлера изменяются
по определённым законамккккккккккккф
. ![]() (9.8) которые называются уравнениями
вращения.
(9.8) которые называются уравнениями
вращения.
На примере вращающегося волчка можно
лучше разобраться в этих углах Эйлера
(рис. 9.6). Ось волчка
![]() описывает конус вокруг неподвижной оси
описывает конус вокруг неподвижной оси![]() .
Это вращение определяется углом
.
Это вращение определяется углом![]() (говорят: волчок совершает прецессию).
Отклонение оси волчка от вертикали –
угол нутации
(говорят: волчок совершает прецессию).
Отклонение оси волчка от вертикали –
угол нутации![]() .
.
А
Рис. 9.6.![]() ,
,
определяемое углом
![]() – собственное вращение.
– собственное вращение.
2) Теорема Даламбера – Эйлера. Мгновенная ось вращения.
П
Рис. 9.7.
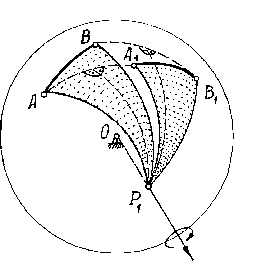
Рис. 9.7.![]() (рис. 9.7). Покажем у тела какие-нибудь
две точки
(рис. 9.7). Покажем у тела какие-нибудь
две точки![]() и
и![]() ,
расположенные на этой сфере. Соединим
их по сфере дугой наибольшего радиуса
(кратчайшее расстояние между точками).
Переместим тело в новое положение.
Точки, а значит и дуга, займут положение
,
расположенные на этой сфере. Соединим
их по сфере дугой наибольшего радиуса
(кратчайшее расстояние между точками).
Переместим тело в новое положение.
Точки, а значит и дуга, займут положение![]() и
и![]() .Соединим
точки
.Соединим
точки![]() и
и![]() и
и![]() дугами большого радиуса
дугами большого радиуса![]() и
и![]() .
Посередине этих дуг проведём им
перпендикулярные дуги и найдём их
точку пересечения
.
Посередине этих дуг проведём им
перпендикулярные дуги и найдём их
точку пересечения![]() .Соединим
эту точку
.Соединим
эту точку![]() с точками
с точками![]() .
Получим два сферических треугольника
.
Получим два сферических треугольника![]() и
и![]() ,
расположенных на этой сфере. Эти два
треугольника равны, как треугольники
с равными сторонами (
,
расположенных на этой сфере. Эти два
треугольника равны, как треугольники
с равными сторонами (![]() ,
а
,
а![]() и
и![]() – как дуги равноудалённые от
перпендикуляров). Так как эти два
треугольника расположены на одной сфере
и имеют общую вершину
– как дуги равноудалённые от
перпендикуляров). Так как эти два
треугольника расположены на одной сфере
и имеют общую вершину![]() ,
то их можно совместить поворотом сферы,
а значит и тела, вокруг прямой
,
то их можно совместить поворотом сферы,
а значит и тела, вокруг прямой![]() .
.
Поэтому можно сделать вывод, что тело
с одной неподвижной точкой можно
переместить из одного положения в другое
поворотом вокруг некоторой оси, проходящей
через неподвижную точку
![]() .Это утверждение – есть теорема
Даламбера-Эйлера.
.Это утверждение – есть теорема
Даламбера-Эйлера.
К
Рис. 9.7.![]() такого перехода мало, то это перемещение
будет близко к действительному. А при
такого перехода мало, то это перемещение
будет близко к действительному. А при![]() можно предположить, что для данного
момента времени тело поворачивается
вокруг некоторой осиР, проходящей
через неподвижную точку
можно предположить, что для данного
момента времени тело поворачивается
вокруг некоторой осиР, проходящей
через неподвижную точку![]() ,
вращаясь вокруг неё с угловой скоростью
,
вращаясь вокруг неё с угловой скоростью![]() .
Конечно, для каждого другого момента
времени эта ось расположена иначе.
Поэтому ось
.
Конечно, для каждого другого момента
времени эта ось расположена иначе.
Поэтому ось![]() называютмгновенной осью вращения,
а угловую скорость
называютмгновенной осью вращения,
а угловую скорость![]() –мгновенной угловой скоростью,
вектор которой направлен по оси.
–мгновенной угловой скоростью,
вектор которой направлен по оси.
Рис. 9.8.
3) Скорость точек тела.
П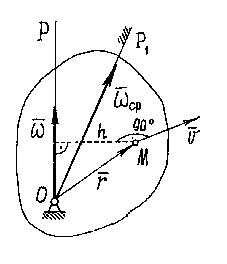 о
теореме Даламбера-Эйлера за малое время
о
теореме Даламбера-Эйлера за малое время![]() движение тела можно представить как
вращение вокруг неподвижной оси
движение тела можно представить как
вращение вокруг неподвижной оси![]() с некоторой угловой скоростью
с некоторой угловой скоростью![]() (рис.9.8). Тогда скорость
точки
(рис.9.8). Тогда скорость
точки![]() ,
по (9.5),
,
по (9.5),
Рис. 9.8.![]()
![]() ,
угловая скорость
,
угловая скорость![]() будет приближаться к мгновенной угловой
скорости
будет приближаться к мгновенной угловой
скорости![]() ,
направленной по мгновенной оси вращения
,
направленной по мгновенной оси вращения![]() ,
а скорость точки
,
а скорость точки![]() -
к истинному значению:
-
к истинному значению:
![]() =
=
![]() . (9.9)
. (9.9)
Н
Рис. 9.8.![]() ,
в нашем случае – по мгновенной оси
вращения
,
в нашем случае – по мгновенной оси
вращения![]() .
Поэтому скорость точки можно определить
как скорость её при вращении тела вокруг
мгновенной оси
.
Поэтому скорость точки можно определить
как скорость её при вращении тела вокруг
мгновенной оси![]() .
Величина скорости
.
Величина скорости![]() (рис. 9.8).
(рис. 9.8).
О
Рис. 9.9.![]() .
Иногда её можно найти, если удастся
обнаружить у тела хотя бы ещё одну
точку, кроме
.
Иногда её можно найти, если удастся
обнаружить у тела хотя бы ещё одну
точку, кроме![]() ,
скорость которой в данный момент
равна нулю, и провести ось
,
скорость которой в данный момент
равна нулю, и провести ось![]() из неподвижной точкиOчерез эту точку. Так как мгновенная ось
вращения – геометрическое место
точек, скорости которых равны нулю в
данный момент времени.
из неподвижной точкиOчерез эту точку. Так как мгновенная ось
вращения – геометрическое место
точек, скорости которых равны нулю в
данный момент времени.
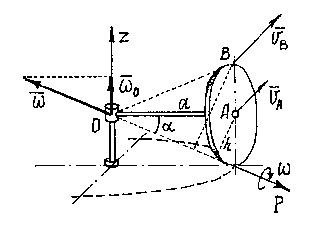
Пример 9.2.Водило![]() ,
вращаясь вокруг вер- тикальной оси
,
вращаясь вокруг вер- тикальной оси![]() с угловой ско- ростью
с угловой ско- ростью![]() ,заставляет диск ра- диуса
,заставляет диск ра- диуса![]() кататься по горизонтальной плоскости
(рис. 9.9).
кататься по горизонтальной плоскости
(рис. 9.9).
Е
Рис. 9.9.
Рис. 9.10.![]() ,
то движение диска можно назвать вращением
вокруг этой непод- вижной точки
,
то движение диска можно назвать вращением
вокруг этой непод- вижной точки![]() .
.
Так как скорость точки касания диска с
плоскостью равна нулю, то мгновенная
ось вращения![]() проходит через эту точку. И вектор
мгновенной угловой скорости
проходит через эту точку. И вектор
мгновенной угловой скорости![]() будет направлен по этой оси.
будет направлен по этой оси.
Точка
![]() вместе с водилом
вместе с водилом![]() вращается вокруг оси
вращается вокруг оси![]() .
Поэтому её скорость
.
Поэтому её скорость![]() (рис. 9.9). Эта скорость определяет
направление вращения диска вокруг оси
(рис. 9.9). Эта скорость определяет
направление вращения диска вокруг оси![]() и направление вектора
и направление вектора![]() .Величина угловой скорости
.Величина угловой скорости![]() (h– расстояние от
(h– расстояние от![]() до оси
до оси![]() ).
Теперь можно найти скорость любой точки
диска, рассматривая его движение как
вращение вокруг оси
).
Теперь можно найти скорость любой точки
диска, рассматривая его движение как
вращение вокруг оси![]() .
Так, например, скорость точки
.
Так, например, скорость точки![]()
![]() .
Так как
.
Так как![]() и
и![]()
![]() ,
то
,
то![]() и
и![]()
4) Ускорение точек тела.
С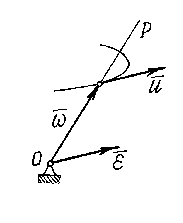 начала
определим угловое ускорение тела
начала
определим угловое ускорение тела![]() .
При движении тела вектор угловой
скорости
.
При движении тела вектор угловой
скорости![]() изменяется и по величине, и по
направлению. Точка расположенная
на его конце будет двигаться по некоторой
траектории со скоростью
изменяется и по величине, и по
направлению. Точка расположенная
на его конце будет двигаться по некоторой
траектории со скоростью![]() (рис. 9.10). Если рассматривать вектор
(рис. 9.10). Если рассматривать вектор![]() как радиус-вектор этой точки, то
как радиус-вектор этой точки, то
![]()
И
Рис 9.10.
![]() . (9.10)
. (9.10)
Этот результат называется теоремой Резаля.
Теперь обратимся к определению ускорения
точек. Ускорение какой-либо точки
![]() тела
тела
![]() , (9.11)
, (9.11)
есть сумма двух векторов.
П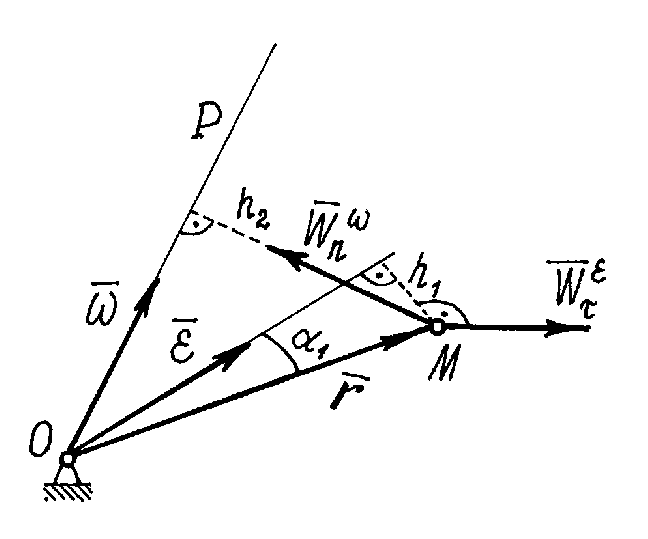 ервый
вектор
ервый
вектор![]() .
Модуль его
.
Модуль его![]() ,
гдеh1–
расстояние от точки
,
гдеh1–
расстояние от точки![]() до вектора
до вектора![]() .Направлен
он перпендикулярно
.Направлен
он перпендикулярно![]() и
и![]() .
Но таким же способом определяет- ся
касательное ускорение. Поэтому первую
составляющую ускорения определяют
как касательное уско- рение,
предполагая, что тело вра- щается
вокруг оси, совпадающей с вектором
.
Но таким же способом определяет- ся
касательное ускорение. Поэтому первую
составляющую ускорения определяют
как касательное уско- рение,
предполагая, что тело вра- щается
вокруг оси, совпадающей с вектором![]() .
И обозначается этот вектор ускорения
так
.
И обозначается этот вектор ускорения
так
![]() (9.12)
(9.12)
В
Рис 9.11.![]() Модуль его
Модуль его![]() ,
но
,
но![]() ,
т.к. векторы
,
т.к. векторы![]() и
и![]() пер- пендикулярны друг другу.
пер- пендикулярны друг другу.
Значит
![]() ,
гдеh2–
расстояние от точкиМдо мгновенной
оси
,
гдеh2–
расстояние от точкиМдо мгновенной
оси![]() ,
до вектора
,
до вектора![]() .
.
Направлен вектор
![]() перпендикулярно
перпендикулярно![]() и
и![]() ,
т.е. так же как вектор нормального
ускорения при вращении вокруг оси
,
т.е. так же как вектор нормального
ускорения при вращении вокруг оси![]() ,
или вектора
,
или вектора![]() .
Поэтому этот вектор ускорения и
обозначают, соответственно, так:
.
Поэтому этот вектор ускорения и
обозначают, соответственно, так:
![]() (9.13)
(9.13)
Итак, ускорение точек тела, вращающегося вокруг неподвижной точки, определяется как сумма двух ускорений:
![]() (9.14)
(9.14)
Этот результат называется теоремой Ривальса.
Заметим, что в общем случае векторы
![]() и
и![]() не совпадают и угол между
не совпадают и угол между![]() и
и![]() не равен
не равен![]() ,
векторы не перпендикулярны друг другу,
как это было при вращении тела вокруг
неподвижной оси.
,
векторы не перпендикулярны друг другу,
как это было при вращении тела вокруг
неподвижной оси.
Пример 9.3.Продолжим исследование
движения диска (пример 9.2). Модуль
угловой скорости
Рис 9.12.![]() Значит вектор
Значит вектор![]() вместе с осью
вместе с осью![]() ,
которая всегда проходит через точку
касания диска с плоскостью, вращается
вокруг оси
,
которая всегда проходит через точку
касания диска с плоскостью, вращается
вокруг оси![]() и описывает конус. ТочкаМна конце
вектора
и описывает конус. ТочкаМна конце
вектора![]() движется по окружности радиуса
движется по окружности радиуса![]() с угловой скоростью ω0. Поэтому
угловое ускорение диска
с угловой скоростью ω0. Поэтому
угловое ускорение диска![]() .
.
Разработал ст.преподаватель кафедры «Прикладная механика» Пинчук Э.В.
