4. 2. Трение качения

С

Рис. 7.7.

опротивление движению тела по поверхности появляется не только при скольжении, но и при качении, например, колеса (рис. 7.7). Конечно, сила тре­нияне может препятствовать движению, качению колеса (момент сил относительно точки касания не ра­вен нулю даже при совсем малой силе). Сила трения, образуя с силойпару, будет вращать тело, заставит его катиться по поверхности.

С

Рис. 7.8.

Рис. 7.7.

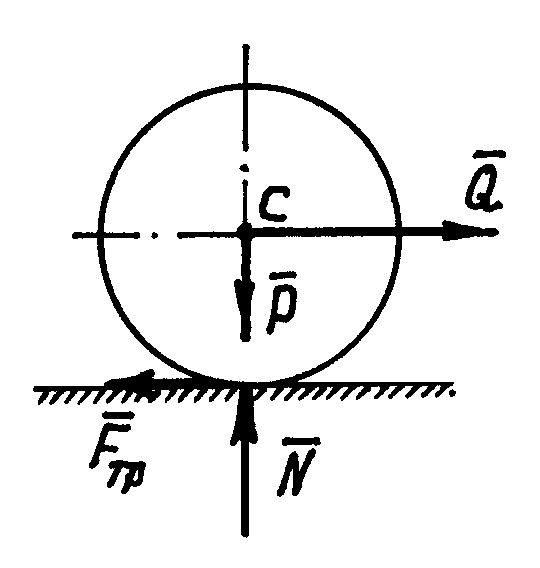
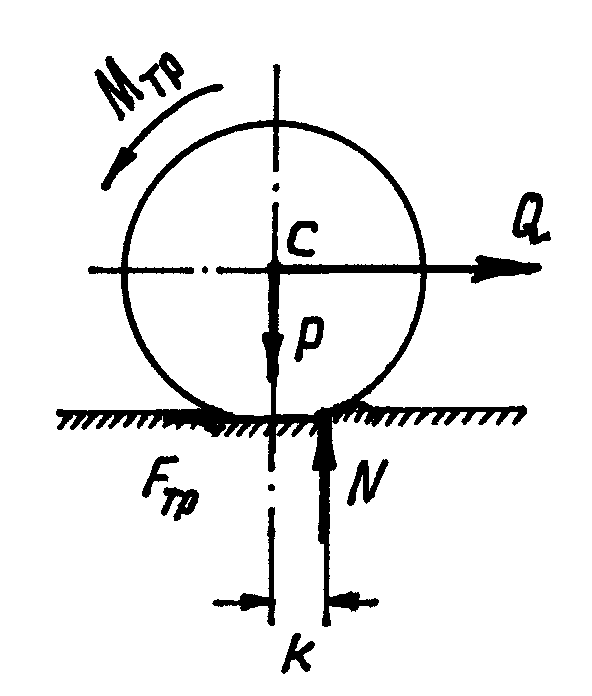
опротивление качению можно объяснить тем, что поверхность и колесо – это не абсолютно твёрдые тела. Они деформируются и поэтому реакция поверх­ности окажется распределённой силой, равнодейст­вующая которойокажется приложенной не под цен­тром колеса, а смещённой вперёд на расстояниеk(рис. 7.8). Силыибудут теперь образовывать пару, ко­торая и препятствует качению тела. Момент этой парыназываетсямоментом трения качения. Он оказывается пропорциональным нормальной реак­ции. Коэффициент пропорциональностиk– называется коэффициентом трения качения. Размерность его – размерность длины (см). Считается, что он зависит только от радиуса колеса и материалов колеса и по­верхности.

Следует ещё раз, специально заметить, что со­противление качению характеризуется не силой, а парой – моментом этой пары (моментом трения качения) (рис. 7.8).

Если колесо катится без скольжения, то сила трения . А так как при равновесии (рис. 7.8);, то.

Поэтому условием качения без скольжения является неравенство или, гдеr – радиус колеса.

2. Кинематика точки

5. 1.Способы задания движения точки

Прежде чем заняться исследованием движения точки, определением характеристик этого движения, надо научиться определять положение точки в пространстве в нужный момент времени.

Для этого существует несколько способов задания движения.

1) Естественный способ.

Ч

Рис. 8.1.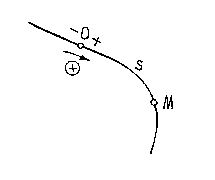

тобы определить движение точки ес­тест­вен­ным способом должно быть заранее за­дано (рис. 8.1): траектория движения точки ( линия, по кото­рой точка движется); начало отсчёта (точка, от кото­рой по траектории отсчитыва­ется расстояниеsдо движущейся точкиМ ) ; на­правление, в ко­тором от­кладываются поло­жительные зна­чения характери­стик движе­ния (указыва­ется стрелкой, либо зна­ками + и − ); закон движенияs = s(t).

Пример 8.1.Точка движется по прямой линии, по закону(рис. 8.2).

В начале движения, при Положение точкиназы­ваетсяначальным положением. При

К

Рис. 8.2.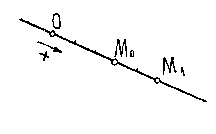

онечно, заточка прошла расстоя­ниеM₀M₁=2 см. Так чтоs– это не путь пройден- ный точ­кой, а расстояние от начала отсчёта до точки.

2) Координатный способ.

Этим способом положение точки в какой либо системе координат определяется её координатами (рис. 8.3). При движении точки эти координаты изменяются. Поэтому, чтобы определить положение точки в нужный момент времени, должны быть заданы координаты как функции

времени :(8.1)

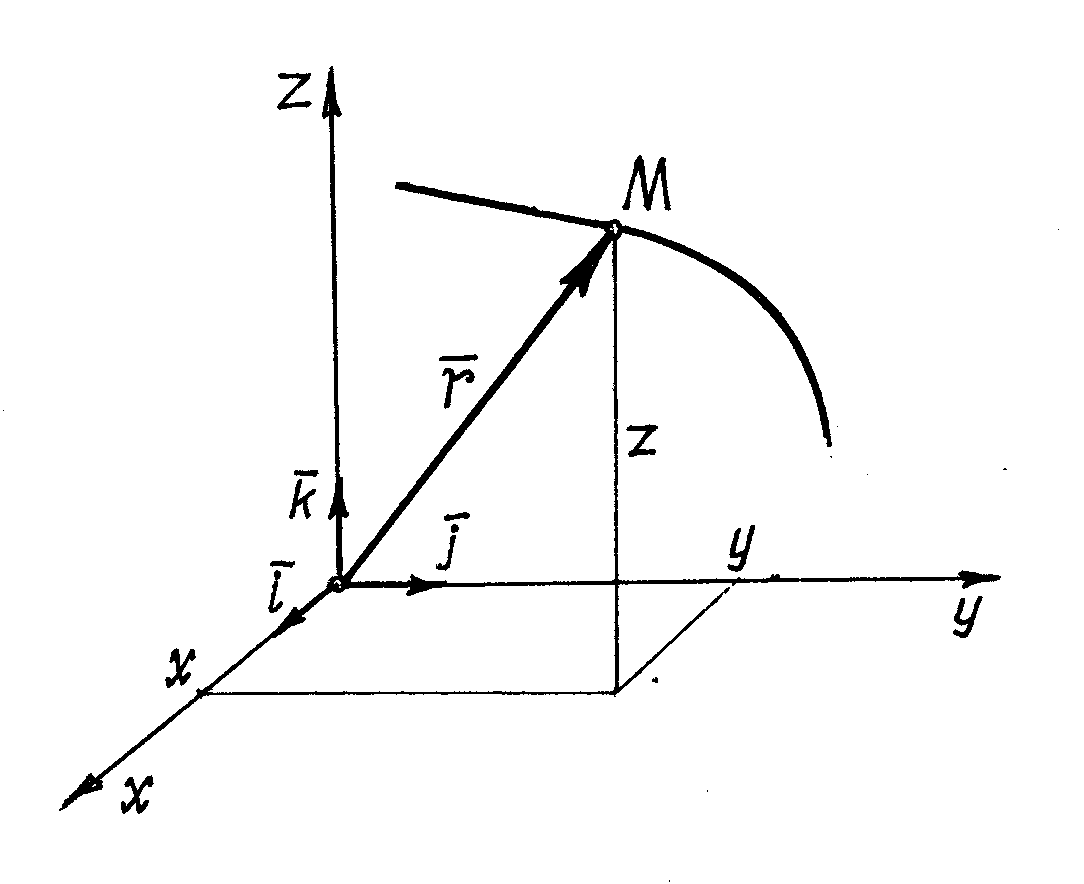
Эти функции называются уравнениями движения точки.

Уравнения движения позволяют определить не только положение точки в любой момент времени, но и все характеристики движения, в том числе и траекторию движения.

Ч

Рис. 8.3.

тобы получить уравнение траектории надо из уравнений движения исключить параметр.

Пример1.2.Движение точки задано уравнениями

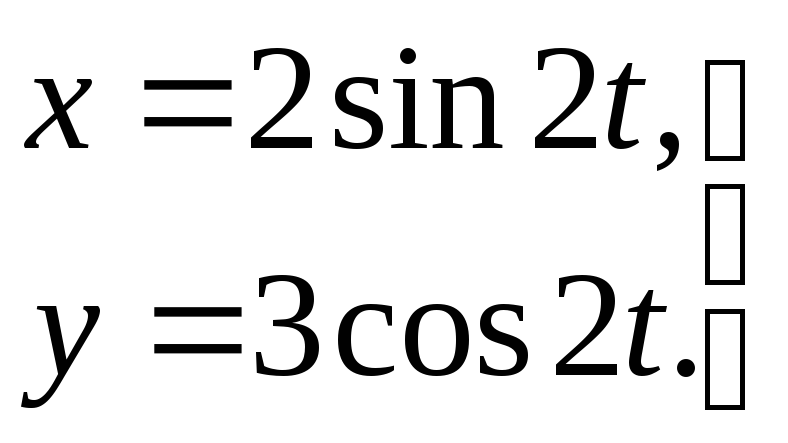
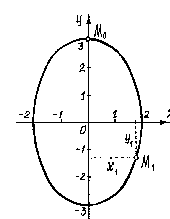
Ч

Рис. 8.4.

тобы исключить время, параметрt, найдём из первого уравненияиз второгоЗатем возведём в квадрат и сложим. Так какполучимЭто урав- нение эллипса с полуосямии(рис. 8.4).

Начальное положение точки (при) определяется координатамиЧерезточка будет в положениис координатами

Примечание.

Движение точки может быть задано с помощью и других координат. Например, цилиндрических или сферических. Среди них будут не только линейные размеры, но и углы. При необходимости, с заданием движения цилиндрическими и сферическими координатами можно познакомиться по учебникам.

3) Векторный способ.

Положение точки можно определить заданием вектора , проведённого из неподвижной точки, предполагая, что точка находится на конце этого вектора (рис. 8.3). Этот вектор называетсярадиусом-вектором точки . Конечно, чтобы определить положение точки в любой момент времени, радиус-вектор должен быть задан как функция времени

Нетрудно установить зависимость между векторным и координатным способами задания движения.

Разложим вектор на составляющие по осям координат:

где- проекции вектора на оси;– единичные векторы направленные по осям, орты осей. Так как началовектора находится в начале координат, то проекции вектора будут равны координатам точки.Поэтому

(8.2)

Траектория движения точки – это линия, которую описывает конец изменяющегося радиуса-вектора. Эта линия называетсягодографом вектора.