3. 1. Трение скольжения

Известно, что поверхности, с которыми соприкасаются тела, не являются абсолютно гладкими. Чтобы сдвинуть тело приходится приложить к нему опре­делённую силу. Это сопротивление, препятствующее скольжению тела, называ­ется трением скольжения. А сила, возникающая при этом – силой трения скольжения –.

Основные закономерности, позволяющие оценить это сопротивление, ус­тановлены опытным путём.

Е

Рис. 7.1.

сли к телу, лежащему на горизонтальной плоскости, приложить силу(рис. 7.1), можно обнаружить, что при достаточно малой силе тело ещё остаётся неподвижным. Силабудет уравновешиваться силой трения,т.е.. Но в некоторый момент, когда силаQдостигнет определённого значе­нияQ*,начнётся скольжение тела.

Дальнейшее увеличение силы Qне изменит величину силы трения.

График зависимости силы тре­ния отQдан на рис. 7.2. Заме­чено, что до начала скольже­ния сила трения (сила трения покоя) достигнет некоторого значенияF*,большего чем при последующем скольжении.

Э

Рис. 7.2.

то хорошо знают профессио­налы-шоферы, которые не допус­кают про­буксовки колёс при тор­можении или при трогании с места.

Установлено, что при сколь­же­нии сила трения пропорцио­нальна величине нормальной реакции N:

. (7.1.)

Коэффициент пропорцио­нальности fназываетсякоэффи­циентом трения скольжения.Этот коэффициент определяется опыт­ным пу­тём. Величина его оказыва­ется0< f 1. Считается, что он зависит только от материала, из которого изготовлены трущиеся поверхности и от фи­зического состояния их (чис­тоты обработки, смазки и т.п.). При необходимости провести точные рас­чёты, стараются учесть известные зависимости коэффици­ента тренияfот скорости, от температуры и пр. Методику таких расчётов можно найти в специальной литературе.

Естественно, трение скольжения увеличи­вает область устойчивости рав­новесного состоя­ния конструкции. Хотя решение задач несколько усложняется появлением дополнительной неиз­вестной реакции поверхности –.

Обычно исследуют равновесное состояние системы на границе между покоем и скольже­нием, полагая силу трения , и решают задачу обычным, известным методом – состав­лением уравнений равновесия.

Пример 7.1.На какое максимальное рас­стояниеаможет подняться человек по лестнице, приставленной к стене (рис. 7.3)? Если вес чело­века –Р, коэффициент трения скольжения между лестницей и стеной –, между лестни­цей и полом –.

Рассматриваем равновесие лестницы с че­ловеком. Показываем силу , нормальные реак­цииии добавляем силы трения:и. Полагаем, что чело­век находится на расстоянии, при большем значении которого начнётся движение лестницы. Состав­ляем уравнения равновесия.

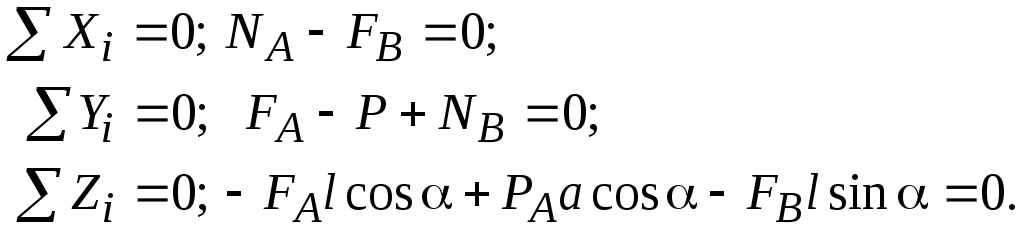
Подставив значения сил трения и решив систему уравнений, получим

Теперь можно определить и угол под которым надо поставить лестницу, чтоб добраться до стены. Полагая , получим, после преобразований,и

При исследовании равновесия тел с учётом трения скольжения иногда бывает полезным вос­пользоваться понятием угла трения и конуса тре­ния.

У

Рис. 7.4.

глом тренияназывается уголмежду нор­мальной реакциейи полной реакцией плоскости(рис. 7.4). Если направление вектора силы трения на плоскости меняется, то векторбудет направлен по соответствующей образующей конуса, который называетсяконусом трения.

Очевидно

Заметим, что если равнодействующая всех активных сил (всех кроме реакций) направлена под углом(рис. 7.4), то нормальная реакция, а сила трения. Для того, чтобы началось скольжение должно выполнятся условие. или. И так как, то . Значит уголдолжен быть больше угла. Следовательно, если силадействует внутри угла или конуса трения (), то как бы не была ве­лика эта сила, скольжение тела не произойдёт. Такое условие называется усло­вием заклинивания, самоторможения.

Мы рассмотрели скольжение твёрдых тел по поверхности. Но нередко встречается скольжение гибких тел по неплоской по­верхности. Например, нежелательное проскальзывание в ременной передаче ремня по шкиву, или троса, каната, на­мотанного на неподвижный цилиндр.

Пусть имеется нить, перекинутая че­рез неподвижную цилиндрическую поверх­ность (рис. 7.5). За счёт сил трения натяже­ние левого и правого концов этой нити бу­дут различными.

Рис. 7.5.

Рис. 7.6.

Предположим, что нормальная реак­ция и сила трения распределяются равно­мерно по дуге контакта нити на цилиндре. Рассмотрим равновесие участка нити дли­ной . (рис. 7.6). На левом конце этого участка натяжение, на пра­вом. Составляем уравнения равновесия, проектируя силы на оси:

Так как угол - малая величина, то полагаемС учётом этого из уравнений находими, так как, имеемилиИнтегрируя, получим. Или

. (7.2.)

Этот результат называется формулой Эйлера.

Например, если нить перекинута через неподвижный шкив и , а ко­эффициент трения, то отношение натяжений. А, обернув цилиндр один раз (),то есть можно удержать груз на другом конце нити силой почти в три раза меньшей веса тела.