3. Закон равенства действия и противодействия.

Силы взаимодействия двух материальных точек равны по модулю и противоположно направлены по прямой, проходящей через эти точки.

.

4. Закон независимости действия сил.

При одновременном действии на материальную точку нескольких сил, ускорение точки в инерциальной системе отсчета от каждой отдельной силы не зависит от остальных сил, а полное ускорение точка равно векторной сумме ускорений, получаемых точкой от действия каждой отдельной силы.

,, …,; (2)

. (3)

Следствие.

Сложим левые и праве части выражений (2) и учтем (3), получим:

. (4)

Выражение (4) – основное уравнение динамики точки при действии на нее нескольких сил.

1. Динамика материальной точки

1.1. Дифференциальные уравнения движения материальной точки

Рассмотрим движение некоторой материальной точки Мв инерциальной системе отсчета.

. (5)

Введем радиус-вектор точки Мотносительно начала системы координат. Как известно из кинематики . Тогда уравнение (5) перепишется в виде . (6)

Полученное уравнение (6) – дифференциальное уравнение движения точки в векторной форме. Его же можно переписать следующим образом:

. (6')

Спроецируем уравнение (5) на оси координат:

,,.

Из кинематики известно, что

,,,

тогда

,,, (7)

,,. (7')

Уравнения (7) и (7') – дифференциальные уравнения движения точки в координатной форме (в декартовой системе координат).

Рассмотрим движение точки по заданной траектории. Положение точки на траектории определяется дуговой координатой. В точке вводятся естественные оси.

Проецируем уравнение движения (5) на естественные оси: ,,. Согласно кинематике: ,,(т.к. ускорение всегда лежит в сопряженной плоскости).

Тогда, получаем

,,. (8)

Выражения (8) – дифференциальные уравнения движения точки в естественных осях (естественные дифференциальные уравнения).

Центр тяжести

1. 1. Сложение параллельных сил. Центр параллельных сил

Пусть даны две параллельные силы и, направленные в одну сторону и приложенные к точками(рис. 6.1).

Конечно, величина их равнодейст­вующей . Вектор её параллелен силам и направлен в ту же сторону. С помощью теоремы Вариньона (5.8) най­дём точку приложения равнодействую­щей – точкуС. По этой теореме . Значит

Рис. 6.1.

О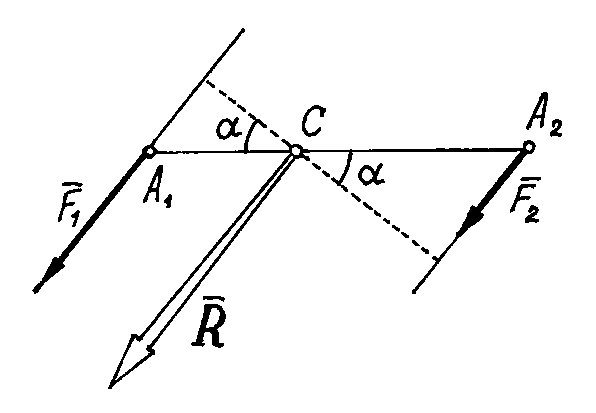тсюдаТо есть точка приложения равнодействующей делит расстояние между точкамиина части обратно пропорцио­нальные силам.

Если параллельные силы направ­лены в противоположные стороны (рис. 6.2), то аналогично можно дока­зать, что равнодействующая по вели­чине будет равна разности сил: (если), параллельна им, направлена в сторону большей силы и расположена за большей силой – в точкеС. А расстояния от точки С до точек приложения сил обратно пропорциональны силам:

С

Рис. 6.2.

ледует заметить, что если точка приложения равнодействующей располо­жена на одной прямой с точкамии, точками приложения сил, то, при повороте этих сил в одну сторону на одинаковый угол, рав­нодействующая также повернётся вокруг точки приложе­нияС в том же направлении, и останется параллельной им.

Такая точка приложения равнодействующей называется центром параллельных сил.

К

Рис. 6.2.

онечно, если хотя бы одну из сил перенести по своей линии дей­ствия в другую точку, то и точка приложения равнодействующей, центр параллельных сил, тоже переместится по линии действия.

Следовательно, положение центра параллельных сил зависит от координат точек приложения сил.

Центром нескольких параллельных сил, найденный последовательным сложением каждых двух сил, будем называть точку С, радиус-вектор которой определяется формулой

, (6.1)

где- радиусы-векторы точек приложения сил;– вели­чина равнодействующей параллельных сил, равная алгебраической сумме этих сил (знак силы определяется направлением, которое заранее выбирается и считается положительным).

Используя (6.1), нетрудно найти координаты центра параллельных сил. Если радиусы-векторы откладывать из начала координат, то проек­ции радиусов-векторов точек на оси будут равны их координатам. По­этому, проектируя векторное равенство (6.1) на оси, получим

(6.2)

где– координаты точек приложения сил.