1.4. Ускорение точки при естественном способе задания движения.

Частные случаи движения точки

Скорость точки .

Ускорение точки ;

;;;

.

Из последнего уравнения следует, что вектор ускорения точки находится в соприкасающейся плоскости.

Обозначим через – нормальная составляющая ускорения точки;– касательная составляющая ускорения точки. Проекции– проекция ускорения на единичный вектор(касательное ускорение) – может быть положительным и отрицательным;– проекция ускорения на единичный вектор(нормальное ускорение) – всегда положительна.

Угол α образованный полным ускорением и главной нормалью равен

.

Если > 0 и> 0, то точка движется ускоренно в положительном направлении. Если< 0 и< 0, то точка движется ускоренно в отрицательном направлении. Если> 0 и< 0, то точка движется замедленно в положительном направлении. Если< 0 и> 0, то точка движется замедленно в отрицательном направлении.

Касательное ускорение , если, т.е. когда точка совершает равномерное движение или в моменты времени, в которые скорость достигает экстремума.

Нормальное ускорение , если, т.е. точка движется по прямой линии или в точках перегиба траектории; в моменты времени, когда точка меняет направление движения, т.е..

Касательное ускорение характеризует изменение скорости по величине, а нормальное – по направлению.

Получим еще формулы для определения ускорений. Продифференцируем обе части выражения :

;

;

;

;;.

Рассмотрим частные случаи движения точки.

1. Равномерное движение: ,;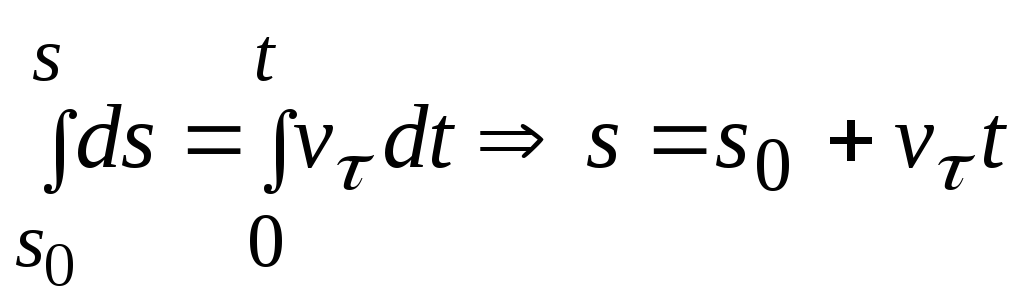– закон равномерного движения точки.

2. Равнопеременное движение: ,;;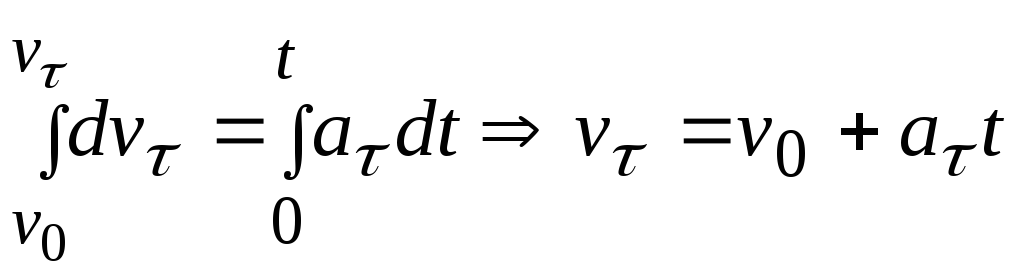– закон равнопеременного движения точки.

2. Простейшие движения твердого тела

2.1. Степени свободы твердого тела

Числом степеней свободы твердого теланазывается число независимых параметров, определяющих положение тела в рассматриваемой системе отсчета.

Свободное твердое тело в пространстве имеет 6 степеней свободы. Положение тела определяется положением любых трех его точек, не лежащих на одной прямой. Для этих трех точек будем иметь 9 координат, которые не являются независимыми, поскольку связаны тремя уравнениями: расстояния между точками не должны изменяться, т.е. M₁M₂=l₁,M₂M₃=l₂,M₁M₃=l₃. Поэтому независимыми будут только 9 – 3 = 6 координат.

Свободная точка имеет три степени свободы. Точка на поверхности будет иметь 2 степени свободы, поскольку три координаты точки связаны уравнением поверхности. Если точка находится на кривой, то она имеет 1 степень свободы.

2.2. Теорема о проекциях скоростей точек твердого тела

Теорема.При любом движении проекции скоростей двух точек твердого тела на прямую, проходящую через эти точки, одинаковы.

Доказательство.Возьмем в твердом теле две произвольные точкиАиВ. Определим их положение относительно неподвижной точкиОвекторамии. Выразимчерез:

,

.

Обозначим и скалярно возведем в квадрат обе части последнего равенства:. Продифференцируем обе части равенство по времени:

,.

, т.к. это расстояние между двумя точками твердого тела, поэтому. Следовательно,

,,,,,.