4.5. Центр тяжести и методы его нахождения

Рассмотрим твердое тело и разобьем его на бесконечное число элементарных частей, каждая из которых будет иметь бесконечно малый объем. Введем в рассмотрение силу тяжести каждой такой части. По своей природе эти силы сходятся к центру земли, поэтому на данное твердое тело действует система параллельных сил тяжести, направленных в одну сторону.

Центром тяжести тела называется центр параллельных сил тяжести элементарных частичек тела при стремлении числа разбиений к бесконечности.

Пусть С– центр параллельных сил. Сила тяжести всего тела, радиус-вектор центр параллельных сил, где– радиус-вектор частички тела.

Для однородного тела

,

, следовательно. Если устремить число разбиений к бесконечности.

Координаты записываются следующим образом:

,,,

,,.

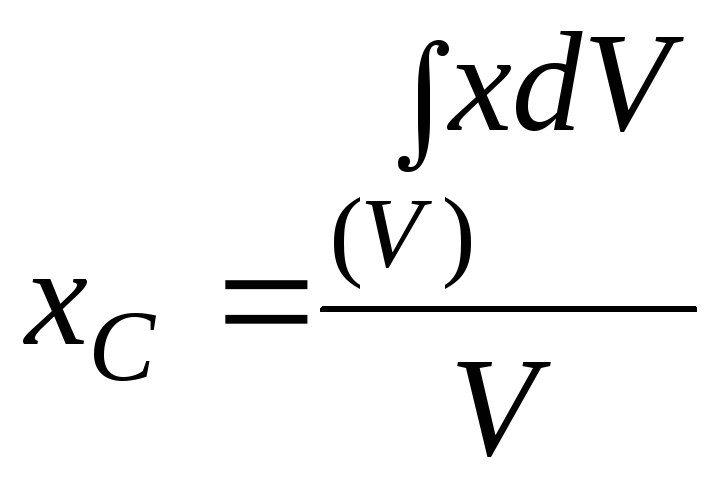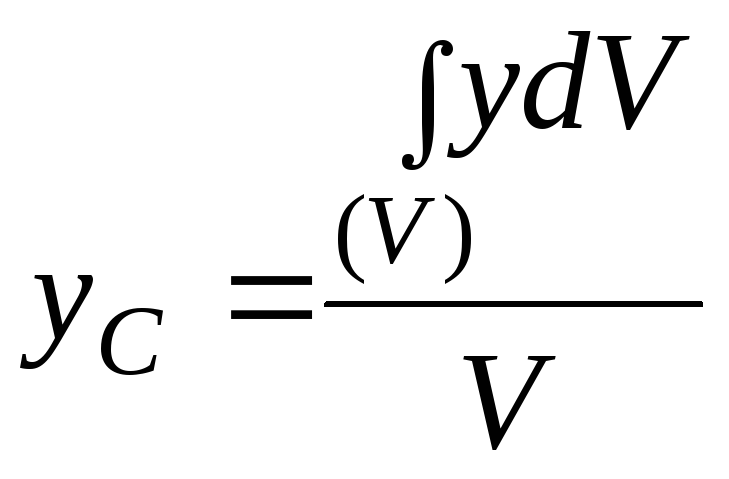Если тело имеет форму тонкой поверхности (т.е. один из размеров будет несоизмерим по сравнению с двумя другими), тогда можно ввести силы тяжести в виде:

,,

, где– площади элементарных частей тела;

.

Если два размера малы по сравнению третьем, тогда

,.

Рассмотрим теперь методы нахождения центра тяжести.

1. Метод симметрии: если однородное твердое тело имеет плоскость (ось, центр) симметрии, то центр тяжести тела расположен в плоскости симметрии (на оси симметрии или совпадает с центром симметрии).

2. Метод разбиения на части – применяется в тех случаях, когда тело можно разбить на части, для каждой из которых известно положение ее центра тяжести или ее можно легко определить. Например,

,.

3. Метод отрицательных масс – применяется в тех случаях, когда тело имеет пустые полости (вырезы). Например,

,.

4.6. Определение центров тяжести простейших однородных тел

1. Прямолинейный отрезок.Центр тяжести прямолинейного однородного отрезка располагается на его середине, а неоднородного – на самом отрезке и не может находиться вне прямолинейного отрезка.

2. Площадь треугольника.Центр тяжести площади, ограниченной треугольником, располагается в точке пересечения медиан треугольника на расстоянии 2/3 от вершины.

3. Дуга окружности.Центр тяжести дуги окружности радиусомRи стягиваемым ею центральным угломнаходится на оси симметрии дуги и равен

.

4. Площадь кругового сектора.Центр масс площади кругового сектора с радиусом Rи центральным угломнаходится на оси симметрии сектора и равен

.

5. Объем пирамиды и конуса.Центр тяжести объема конуса или пирамиды (как прямых, так и наклонных) находится на расстоянии 1/4 расстояния от центра масс площади основания до вершины.

6. Объем полушара. Центр масс объема полушара радиусомRнаходится на оси симметрии на расстоянии 3/8Rот его центра.

1. Кинематика точки

1.1. Траектория движения, скорость и ускорение точки

1. Траектория движения. Траекторией движения точкиназывается геометрическое место ее последовательных положений с течением времени в определенной системе отсчета. В разных система отсчетах одна и та же траектория точки будет иметь различную форму.

2. Скорость точки. Рассмотрим точкуМв пространстве. Положение этой точки в каждый момент времени относительно неподвижного центраОбудет определяться радиус-вектором. В момент времениt– положение точкиМ, в момент времениположение точки .

Средней скоростьюточки за времяназывается вектор, где– приращение радиус-вектора. Векторнаправлен по вектору.

Скоростью точки в данный момент времени называется вектор , равный.

Скорость направлена по касательной к траектории движения точки в сторону движения. Скорость характеризует быстроту изменения положения точки в пространстве с течением времени. Размерность скорости .

3. Ускорение точки. Пусть положение точки в момент времениt–М, а ее скорость; в момент времени–положение точки , а ее скорость. Перенесем векториз точки в точкуМ. Построим приращение вектора скорости точкиза время:=+. Введем в рассмотрение вектор– среднее ускорение точки за время. Условноприложим в точкеМ.

Ускорением точки в данный момент времени tназывается вектор

;.

Вектор ускорения точки всегда направлен в сторону вогнутости, т.е. во внутрь траектории. Размерность скорости .

4. Годограф.Годографом переменного вектора называется геометрическое место его концов, если этот вектор откладывать от одной и той же общей точки.

Траектория движения точки является годографом ее радиуса-вектора. Можно построить годограф вектора скорости. Можно утверждать, что производная от переменного вектора по скалярному аргументу – есть вектор, направленный по касательной годографа переменного вектора. Ускорение точки направлено по касательной к годографу скорости точки.