4.Пространственная система сил

4.1. Изменение главного момента при перемене центра приведения

Выберем некоторый центр приведения О и приведем к этому центру силы и получим силу и пару сил:

,.

Возьмем другой центр приведения О₁и приведем систему сил к этому центру:

=,

следовательно главный момент системы сил при перемене центра приведения изменяется на векторный момент главного вектора в старом центре приведения относительно нового центра.

4.2. Инварианты системы сил

Инвариантами системы сил, приложенной к твердому телу, называются величины, не зависящие от центра приведения системы сил.

1. Главный вектор системы сил:

,,,,,.

2. Рассмотрим уравнение

.

Умножим скалярно обе части выражения на , причем левую часть на, а правую – на:

, т.к..

Следовательно – второй инвариант системы сил – произведение главного момента на главный вектор системы сил.

3. Если обозначить через иуглы между главным моментом и главным вектором в одном и в другом центрах приведения и учитывая, что, получим:

,,.

4.3. Частные случаи приведения пространственной системы сил

1. Пусть главный вектор системы сил равен нулю, а главный момент не равен нулю, т.е. и.

В этом случае система сил приводится к одной паре, векторный момент которой равен главному моменту системы сил в данном центре приведения и который не зависит от выбора этого центра.

2. Пусть главный вектор системы сил не равен нулю, а главный момент равен нулю, т.е. и.

В этом случае система сил приводится к равнодействующей, равной главному вектору системы сил, проходящей через центр приведения: =.

3. Пусть главный вектор системы сил и главный момент не равны нулю и эти векторы взаимно ортогональны, т.е. ,и.

В этом случае система сил приводится к равнодействующей, равной главному вектору системы сил, не проходящей через центр приведения: =.

4. Пусть главный вектор системы сил и главный момент не равны нулю и эти векторы не взаимно ортогональны, т.е. ,и.

В этом случае система сил приводится к динаме.

Динамой или силовым винтом называется совокупность силы и пары сил, приложенных к твердому телу, в которой сила коллинеарна векторному моменту пары сил.

5. Пусть главный вектор системы сил и главный момент равны нулю, т.е. и.

Система сил находится в равновесии.

Для пространственной системы параллельных сил справедливы два первых и последний случаи приведения. Третий и четвертый объединяются в следующий: пусть главный вектор системы сил и главный момент не равны нулю, т.е. ,, тогда пространственная система параллельных сил приводится к равнодействующей, равной главному вектору системы сил, не проходящей через центр приведения:=.

4.4. Центр параллельных сил

Рассмотрим твердое тело, к которому приложена система параллельных сил. Проведем через точки приложения сил параллельные прямые, перпендикулярные силам. Повернем все силы системы вокруг полученных осей на один и тот же угол. В результате получим систему, силы которой также параллельны.

Центром параллельных сил называется точка приложения равнодействующей этих сил, не изменяющая своего положения в теле при повороте сил системы вокруг параллельных осей на один и тот же угол.

Получим формулу, определяющую радиус-вектор центра параллельных сил. Будем считать, что рассматриваемая система может быть приведена к равнодействующей. Введем в рассмотрение единичный вектор , направленный параллельно силам системы. Тогда

,.

По теореме Вариньона

,,,

.

Поскольку направление сил произвольно, то – единичный вектор произвольного направления и следовательно

или.

Поскольку , то. Спроецировав на оси координат получаем: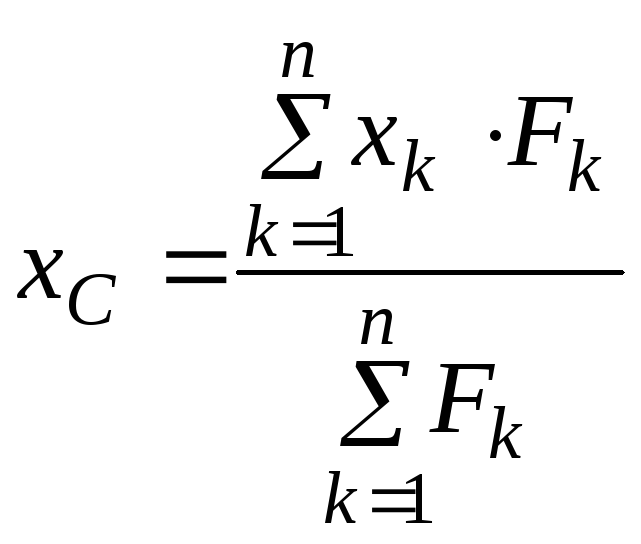,,.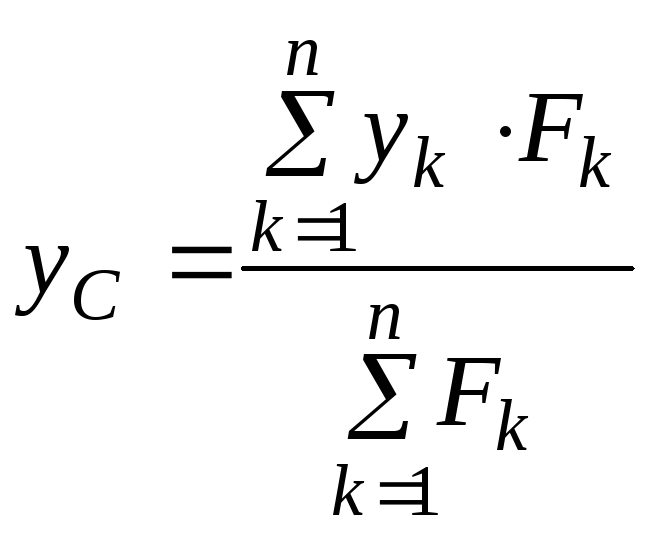