ТВиМС / Стат_Лекц / Стат_Примитивы / СтаЛР_1_Пр

4. Прямая линейной регрессии

   0. Постановка задачи

Пусть имеются два массива числовых данных, значения которых в векторной форме можно записать так:

y_1n^T = (y₁, y₂, … y_n) и x_1n^T = (x₁, x₂, ... x_n).

Графически эти массивы можно представить в виде точек (рис. 1) на плоскости XOY.

X

Рис. 1

Линейная регрессия

Массив y_n1, называемый откликами, рассматривается как случайный, а массив x_n1, называемый предикторами, – не случайный. Для одних и тех же значений предиктора x _j могут быть получено несколько откликов y _i, … y _k. Количество различимых значений предиктора обозначим литерой «m». Очевидно, что j = 1, …, m.

Задача заключается в установлении функциональной зависимости

Y = φ(X) (1)

между величинами Y и X по числовым данным, имеющимся в обоих массивах y_n1 и x _n1.

Такая зависимость называется регрессией Y от X.

Из всего многообразия функций φ выберем преобразование, линейное относительно некоторого вектора параметров

_1k^T = (₀__k-1 k<n 

и вектора регрессоров

F_1k = (f₀ f₁ … f_k-1), (3)

которые являются дифференцируемыми функциями предиктора X, т.е.

f_j = f _j (X). (4)

В векторной форме подобное преобразование имеет вид:

y = F_1k* _k1 (5)

и называется линейной регрессией.

Регрессоры f _j (4) подбираются исследователем по данным графического анализа массивов y_n1 и x_n1, а параметры _k1 «оцениваются» путём обработки этих же массивов данных по определённым алгоритмам.

0. Подбор прямой «линейной регрессии»

В простейшей ситуации уравнение линейной регрессии имеет вид:

Y = f₀*β₀ + f₁*β₁ = β₀ + β₁* X, (6)

т.е. регрессоры f₀ и f₁ равны, соответственно, f₀ = X⁰ = 1, f₁ = X. Уравнение (6) представляет собой математическую модель (ММ) исследуемого явления. Напоминаем, что массивы y_n1 и x_n1 – это числовые данные (простая выборка), полученные в ходе эксперимента.

В процессе наблюдений истинные значения отклика Y_i искажаются неопределённостями ε_i:

y_i = Y_i – ε_i. (7)

Массивы y_n1 и x_n1 позволяют составить систему из n уравнений типа (6):

y_i = β₀ + β₁* x_i – ε_i, (i = 1,2, … n). (8)

Неизвестные параметры β₀ и β₁, а также неопределённости ε_i оцениваются из решения системы (8), дополняемой ограничением наименьших квадратов, которое имеет вид:

 = == min. (9)

Ограничение, определяемое соотношением (9), называется ограничением по методу наименьших квадратов или более лаконично МНК-ограничением.

Обозначим оценки параметров и неопределённостей соответствующими буквами латинского алфавита:

= b, = e.

В таком случае уравнения (8), решаемые с ограничением (9), принимают вид:

y_i = b₀ + b₁* x_i + e_i

. (10)

 = = min

Полученная система (10) решается методом абсолютного экстремума, необходимым условием существования которого является равенство нулю частных производных МНК-ограничения (9) по оцениваемым параметрам:

∂Ψ/∂b₀ = 0 и ∂Ψ/∂b₁ = 0.

Найдём эти производные:

∂Ψ/∂b₀ = – 2(y_i – b₀ – b₁* x_i) = 0

. (11)

∂Ψ/∂b₁ = –2 x_i*(y_i – b₀ – b₁* x_i) = 0

Воспользуемся обозначениями Гаусса для образующихся сумм:

, , , .

Уравнения (11) называются нормальными и, с учётом обозначений Гаусса, могут быть записаны так:

n*b₀ + [x]*b₁ = [y]

. (12)

[x]*b₀ + [x²]*b₁ = [xy]

Матричный эквивалент системы (12) имеет вид

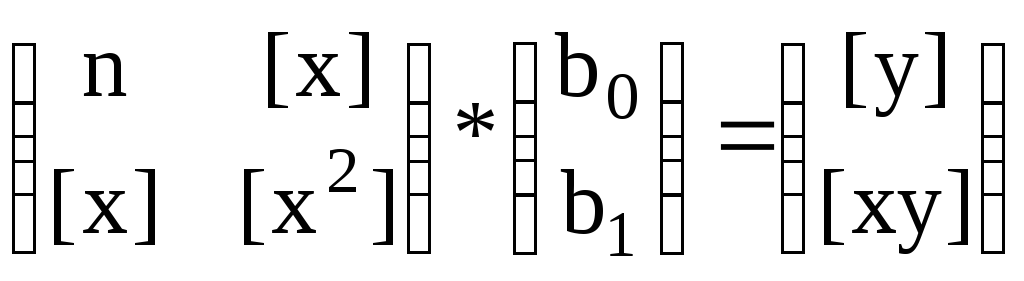. (13)

Решение системы (13), в матричной же форме, имеет вид:

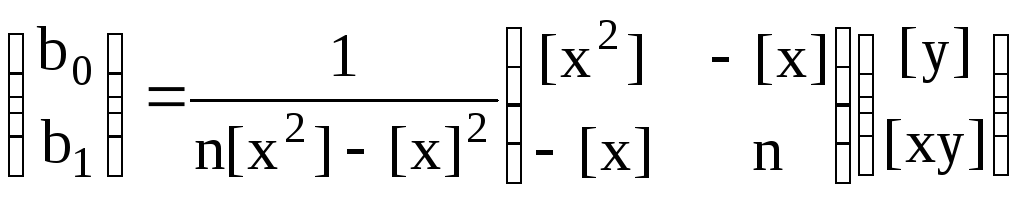. (14)

Прежде чем перейти к алгебраической форме выражения (14), введём дополнительные обозначения, которые упростят вычислительную процедуру:

, . (15)

Окончательно, решение системы (14) можно записать так:

b₀ =

. (16)

b₁ =

Вычисление параметров по формулам (14) или (16) контролируется по формуле связи, вытекающей из первого уравнения системы (12):

= b₀ + b₁*. (17)

После контроля оценок параметров b₀ и b₁ мы можем записать уравнение математической модели (6), называемое уравнением регрессии:

ŷ = b₀ + b₁*x. (18)

Оценки неопределённостей e_i, называемые «остатками», могут быть вычислены по формуле (7) с заменой неизвестных истинных значений откликов Y_i соответствующими регрессионными значениями ŷ _i, найденными по уравнению регрессии (18):

e_i = y_i – ŷ _i. (19)

Нахождение остатков контролируется соотношением

[e] = [y] – n*b₀ – [x]*b₁  0, (20)

вытекающим из формулы связи (17) и являющимся гарантией правильности построения уравнения регрессии (18).

0. Дисперсионный анализ модели

Массив откликов y_n1 характеризуется дисперсией σ², оценка которой для случая линейной регрессии вычисляется по формуле (без вывода!):

. (21)

Апостериорные значения дисперсий оценок параметров могу быть получены по диагональным элементам обратной матрицы (14) коэффициентов нормальных уравнений (13):

, (22)

. (23)

Формулы (21) – (23) применимы только для двухпараметрической линейной модели!

0. Проверка статистических гипотез

При создании регрессионной математической модели обычно проверяют следующие нулевые гипотезы:

1. H₀ = {ММ не адекватна измерениям y_n1};

2. H₀ = {Регрессия не знàчима};

3. H₀ ={Параметр b_j не знàчим};

4. H₀ = {ММ не накрывает контрольную (ые) точку (и)}.

0. Гипотеза о неадекватности ММ

Гипотеза H₀ = {²_L ≠ ²_e} о неадекватности модели проверяется путём сопоставления между собой различных оценок дисперсии откликов σ². Дисперсия «подгонки»

, (24)

полученная по уклонениям регрессионных значений ŷ_i от локальных центров наблюдений сопоставляется с дисперсией «чистой ошибки»

, (25)

вычисленной по уклонениям измеренных значений y_i от тех же локальных центров .

Поскольку оценки и для дисперсии σ² получены по данным одной и той же простой выборки y_n1, то их сравнение может быть осуществлено по F-критерию на уровне значимости α с числами степеней свободы ν₁ = m – k и ν₂ = n – m. Здесь n – это число откликов, m – количество локальных центров, а k – число параметров модели. Соответствующий тест – это отношение дисперсии «подгонки» к дисперсии «чистой ошибки»:

t_Э = / . (26)

Предельное значение данного теста – это квантиль F-распределения на уровне значимости α:

t_П = arg(F_{m-k; n-m} = α). (27)

Теперь, если t_Э > t_П, то гипотеза о неадекватности модели H₀ = {²_L ≠ ²_e} отвергается.

Примечание. Поскольку квантиль F-распределения всегда больше единицы, т.е. F_ν1;ν2>1, то в случае, когда t_Э = / <1, мы можем не определять квантиль (27). В таком случае гипотеза H₀ = {²_L ≠ ²_e} о неадекватности модели не будет отвергнута на любом уровне значимости α.

0. Гипотеза о незначимости регрессии

Гипотеза H₀ = { = } о незначимости регрессии определяется с использованием ещё двух оценок дисперсии откликов σ²:

1) среднего квадрата регрессии

, (28)

найденного по разностям регрессионных значений ŷ_i и общего среднего , и

2) дисперсии остатков

, (29)

полученной по уклонениям измерений y_i от соответствующих регрессионных значений ŷ_i.

Здесь так же используется F-критерий на том же уровне значимости α, но с другими степенями свободы: ν₁ = 1 и ν₂ = n – 2. Соответствующий тест – это отношение дисперсии «регрессии» к дисперсии «остатков»:

t_Э = / . (30)

Предельное значение теста t_Э – это квантиль F-распределения:

t_П = arg(F_{1; n-2} = α). (31 )

Теперь, если t_Э > t_П, то гипотеза H₀ = { = } о незначимости регрессии отвергается.

0. Гипотезы о незначимости параметров ММ

Гипотезы H₀ = {β₀ = 0} и H₀ = {β₁ = 0} о незначимости параметров ММ проверяются с помощью статистик, использующих МНК-оценки параметров и средние квадратические ошибки (СКО) этих оценок:

t_Э = |b_j| / m_bj. (32)

Результаты сопоставляются с квантилью t-распределения Стьюдента

t_П = t_{n-2; 1-α/2} = arg(S_n-2 = 1 – α / 2). (33)

Формулы (22) и (23) для квадратов СКО оценок параметров b₀ и b₁ были получены выше.

Проверяемая гипотеза отвергается, когда t_Э > t_П.

Если хотя бы одна из этих гипотез не отвергнута, то ММ должна быть изменена и вновь подвергнута всем предыдущим проверкам.

0. ММ накрывает контрольные точки

При построении ММ по данным эксперимента рекомендуется часть собранной информации (1% – 5%) зарезервировать в качестве контрольных данных. Дальнейшая процедура проверки эффективности построенной ММ заключается в следующих шагах.

У каждой контрольной точки {x_k; y_k} её отклик y_k заменяется регрессионным значением ŷ_k (18). Далее, используя эту точечную оценку, на уровне значимости α строят доверительный интервал

I_k = { y_k^H; y_k ^B}, (34)

нижняя и верхняя границы которого вычисляются в предположении Стьюдентовского распределения регрессионной оценки ŷ_k:

y_k^H = ŷ_k – t_{n-2; 1-α/2}*m_ŷk , (35)

y_k^B = ŷ_k + t_{n-2; 1-α/2}*m_ŷk , (36)

где

m_ŷk = μ*. (37)

Если интервал (34) накрывает значение контрольного отклика y_k, то предположение H₀ = {ММ не накрывает контрольную точку} отвергается.

Дополнительно для линии регрессии (18) можно построить доверительную область, определяемую тремя парами нижних y_H и верхних y_B границ, вычисляемых в точках {x_min; ŷ_min }, {;} и {x_max; ŷ_max }:

y^H = ŷ – t_{n-2; 1-α/2}*m_ŷ , (38)

y^B = ŷ + t_{n-2; 1-α/2}*m_ŷ . (39)

Здесь

m_ŷ = μ*. (40)

Через точки {y^B_min; ^B; y^B_max} и {y^H_min; ^H; y^H_max} проходят кривые, представляющие собой верхнюю и нижнюю границы доверительной области. Точки, которые были использованы для построения регрессионной модели (18) должны находиться внутри области. Что касается контрольных точек, то достаточно, чтобы их доверительные интервалы (34) пересекались с доверительной областью прямой линейной регрессии.