3.2.3 Интервальные оценки.

Точечные оценки, рассмотренные в предыдущих параграфах, характеризуются нулевой вероятностью своего появления, оставаясь возможными событиями. Этот теоретический «недостаток» точечных оценок легко устраняется путем введения интервальных оценок.

Интервальная оценка параметра а представляет собой доверительный интервал (ДИ) I_= ]a_H; a_B[. Его нижняя (a_H) и верхняя (a_B) доверительные границы определяются с использованием числового значения доверительной вероятности  или уровня значимости  = 1 – γ, назначаемых заранее.

Предполагается, что закон распределения ОФ ã = X известен, например, в форме ФР F(x) = P(ã < x), где x – некоторый элемент спектра СВ ã, для которой объективно существующее значение параметра а является её центром рассеивания, т.е. СВ ã – является несмещенной ОФ: E(ã ) = a. Доверительные границы a_H и a_B рассматриваются как элементы спектра СВ ã. Если, дополнительно, представить доверительные границы как уклонения от точечной оценки, введя расстояния ε_H и ε_B, такие что

a_H = ã – ε_H и a_B = ã + ε_B, (216)

то доверительная вероятность  будет соответствовать следующим равновероятным событиям:

1) известная оценка ã попадает с вероятностью  в ДИ, построенный относительно неизвестного положения параметра а –

 = P(a – ε_H < ã < a + ε_B) = 1 – . (217)

2) ДИ, построенный относительно известного значения оценки ã, накрывает неизвестный параметр а с вероятностью  –

 = P(ã – ε_H < a < ã + ε_B) = P(a_H < a < a_B) = 1 – . (218)

Вероятность именно второго события (218) представляет интерес как с практической, так и с теоретической точек зрения.

Выражение (218) иллюстрируется на графике ФР (рис. 3.2):

F(a)

1.0-

P(a_H < a < a_B) =  = 1 –  =

1/2- = F(a_B) – F(a_H)

F(a_H) F(a_B)

0 a_H ã а a_B A

Рис. 3.2 Доверительный интервал.

(Положение параметра a остается неизвестным!)

ДИ может иметь одну границу конечной, а другую – открытой на бесконечность. В таком случае он называется односторонним, в отличие от обычного – двухстороннего.

Перейдем к построению границ ДИ, основываясь на его аналитическом определении (218).

Дано: F(x) =P(ã < x) – ФР оценивающей функции ã, известная с точностью до своих параметров;

 или  – доверительная вероятность или уровень значимости, соответственно.

Найти: нижнюю a_H и верхнюю a_B границы ДИ.

Решение: Однозначное решение задачи возможно лишь при дополнительных ограничениях, т.к. выражение (218) содержит два неизвестных: a_H и a_В. Обычно, используются следующие ограничения:

1)фиксированная граница (нижняя либо верхняя);

2)равновероятность того, что накрываемый параметр окажется левее или правее границ ДИ.

Односторонний интервал является частным случаем двухстороннего, в связи с чем, получим сначала общее решение, опираясь на выражение (218):

P(a_H < a < a_B) =  = 1 –  = F(a_B) – F(a_H).

1. Зафиксировав сначала нижнюю границу a_H, а затем верхнюю a_B, выразим их друг через друга, что и даст нам искомое общее решение:

a_B = arg(F =F(a_H) + , (219)

a_H = arg(F =F(a_B) –  (220)

Для одностороннего ДИ, у которого нижняя граница открыта на бесконечность, получим:

a_H

a_B = arg(F = ) = arg(F = 1 – , (221)

а для интервала, у которого верхняя граница бесконечно удалена:

a_H = arg(F = 1 – ) = arg(F = )

a_B . (222)

2. Симметричный ДИ строится, исходя из равновероятности выхода за его пределы, т.е.

F(a_H) = 1 – F(a_B) = / 2 = (1 – ) / 2,

откуда:

a_H = arg(F = (1 – ) / 2) = arg(F = )

. # (223)

a_B = arg(F = (1 + ) / 2) = arg(F = 1 – )

3.2.3.1 Построение доверительных границ при нормальном

распределении.

Формулы (221) – (223) позволяют находить доверительные границы, при условии, что ФР известна. На практике очень широко используется нормальная ФР, для которой составлены стандартные таблицы (Приложение 2), т.к. многие ОФ удовлетворяют условиям ЦПТ и, следовательно, имеют нормальное распределение. В такой ситуации за параметр положения нормальной ФР принимается точечная оценка ã, т.е. E(ã) = a, а за параметр её рассеивания – выборочный стандарт оценки . По этим параметрам можно перейти к стандартной нормальной ФР, выполняя нормирование (67):

t_i = (a_i – ã) / , (224)

где i – индекс границы.

Из этого соотношения получаем:

a_H = ã + t_H *

. (225)

a_B = ã + t_B *

С другой стороны, формулы (223) позволяют определить стандартизованные границы через заданную доверительную вероятность  или уровень значимости  следующим образом:

t_H = arg(F = (1 – ) / 2) = arg(F = );

t_B = arg(F = (1 + ) / 2) = arg(F = 1 – ).

При этом, в силу того, что стандартная нормальная ФР обладает известным свойством F(t) + F(– t) = 1, стандартизованные границы будут связаны между собой таким соотношением: t_H = – t_B = – t_P, где индекс P означает либо доверительную вероятность , либо уровень значимости  в зависимости от конкретного источника стандартной ФР.

Окончательно, границы двухстороннего ДИ для нормально распределенной ОФ, параметры которой оценены по выборочным данным, можно построить, объединив все полученные результаты:

a_H = ã – t_P *

. (226)

a_B = ã + t_P *

Задача 3.4. Среднее арифметическое из 12-и наблюдений угла равно = 36^o 52' 47,8", а СКО наблюдений, найденная по этим же данным по формуле Бесселя (215), равна m" = 0,9". Полагая обе оценки нормально распределенными, построить с их помощью двухсторонние ДИ для МО и стандарта ГС на уровне значимости  = 0,05.

Решение.

Построение двухстороннего ДИ для МО.

1. Из таблиц стандартной нормальной ФР (Приложение 2) находим для значения функции F(t_P) = (1 – / 2) = 0,975 стандартизованную границу t_P = arg(F = 0,975) = 1,96.

2. По значению СКО m" вычисляем оценку стандарта СА:

= m" / = 0,9"/= 0,26".

3. По формулам (226) находим границы ДИ для МО:

x_H = - t_P * = 36^o 52' 47,8" – 1,96 * 0,26" = 36^o 52' 47,3";

x_B = + t_P * = 36^o 52' 47,8" + 1,96 * 0,26" = 36^o 52' 48,3".

Построение двухстороннего ДИ для стандарта.

1. Стандартизованная граница имеет то же значение t_P = 1,96.

2. По значению СКО m" вычисляем оценку стандарта этой величины s_m по формуле [15]:

s_m ≈ m" / = 0,9" / = 0,19".

3. По формулам (226) находим границы ДИ для стандарта:

s_H = m – t_P * s_m = 0,9" – 1,96 * 0,19" = 0,5" ;

s_B = m + t_P * s_m = 0,9" + 1,96 * 0,19" = 1,3". #

3.2.3.2 Построение доверительных границ

по малым выборкам.

Предположение о нормальности распределения ОФ справедливо тогда, когда оценка строится по выборке, объем которой составляет, по крайней мере, десятки наблюдений. Если же объем выборки не превышает полутора, двух десятков наблюдений, то распределение ОФ может значительно отличаться от нормального и с этим необходимо считаться, чтобы получить более корректные значения доверительных границ. Предполагая, что мы имеем дело с выборкой из нормальной ГС, рассмотрим некоторые распределения ОФ, используемые для этих целей.

3.2.3.2.1 Распределение Пирсона.

Распределение Пирсона (- распределение, хи-квадрат распределение с n степенями свободы) – это распределение суммы квадратов n стандартных нормальных СВ X_i N(0; 1):

= + + … + . (227)

Не останавливаясь на выводе формулы плотности вероятности этого закона, отметим, что он является частным случаем двухпараметрического гамма-распределения [18]:

, . (228)

Для x < 0 плотность вероятности (228) равна нулю.

Первый параметр гамма-распределения  полагаем равным n / 2, где n – число степеней свободы (целое положительное число). Второй параметр гамма-распределения  = 2. При этих условиях функция плотности вероятности - распределения принимает вид:

, .(229)

По определению (227) величина ² не может быть отрицательной. В связи с этим плотность (229) полагается равной нулю, когда ² < 0.

Функция распределения (ФР) закона ² определяется, согласно (50) и с учётом (229), интегралом:

P(²) = 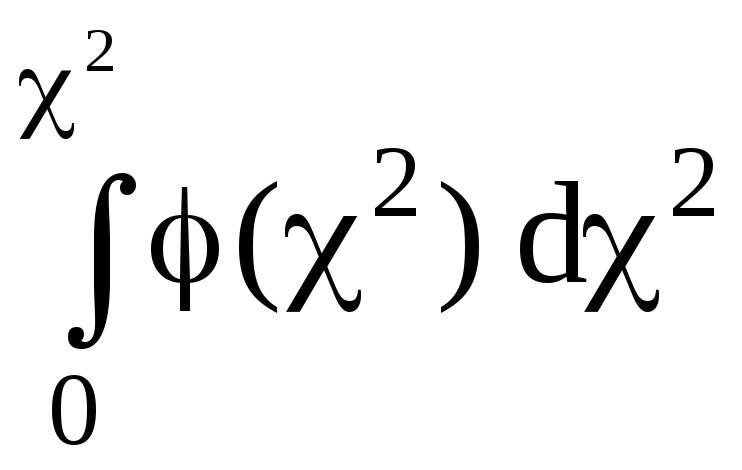, (230)

таблица которого помещена в Приложении 3. Эта таблица позволяет решать статистические задачи, связанные с распределением Пирсона. Например, дробь

= , (231)

где m² – несмещенная выборочная дисперсия (214), которая имеет ²-распределение с (n – k) = r степенями свободы [18]. Здесь k – это число оцениваемых параметров многомерного распределения (в случае простой выборки из одномерного распределения k = 1). Она позволяет построить доверительный интервал для дисперсии генеральной совокупности ²:

(232)

и, несколько смещённый [17], доверительный интервал для стандарта :

. (233)

Таблицы величин (Приложение 5) облегчают построение интервала (233) с границами

s_H = m * _H и s_B = m * _B. (234)