Вопрос 5

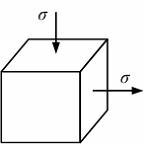
Напряженное состояние элементарного параллелепипеда – …

Ответ 5

плоское (чистый сдвиг)

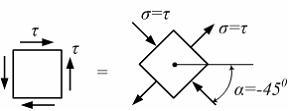При чистом сдвиге (см. рисунок) главные площадки повернуты относительно площадок сдвига на уголТаким образом, чистый сдвиг можно реализовать одновременным растяжением и сжатием в двух взаимно перпендикулярных направлениях равными по величине нормальными напряжениями. Поэтому напряженное состояние, указанное в задании, – чистый сдвиг (плоское напряженное состояние).

Вопрос 6

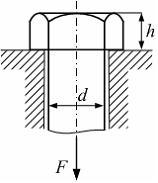
Из расчета на срез минимальная высота головки болта при заданных значениях d и равна …

Ответ 6

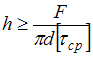
При малой высоте головки болта происходит ее срез по цилиндрической поверхности диаметром d. Примем, что касательные напряжения постоянны по высотеhголовки., тогда.

Задание 10

Вопрос 1

Деформацию стержня, при которой в поперечных сечениях стержня возникает только крутящий момент, называют…...

Ответ 1

Кручением

Вопрос 2

При деформации кручения угол взаимного поворота двух сечений, отнесенный к расстоянию между ними, называется…..

Ответ 2

относительным углом закручивания

Вопрос 3

Стержень круглого поперечного сечения длиной в концевых сечениях нагружен двумя равными и противоположными по направлению моментами . Жесткость поперечного сечения на кручение по длине постоянна. Угол закручивания стержня определяется по формуле….

Ответ 3

Вопрос 4

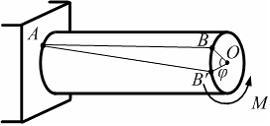
На рисунке показан стержень, работающий на кручение. В процессе закручивания правое кольцевое сечение закручивается на угол . Точкаперемещается в положение, а образующаязанимает положение. Углом сдвига называется угол….

Ответ 4

Вопрос 5

При увеличении момента в два раза наибольшее касательное напряжение….

Ответ 5

не изменится

При увеличении момента в два раза величина максимального крутящего моментане изменяется. Поэтому ине изменятся.

Вопрос 6

Труба испытывает деформацию кручение. Эпюра распределения касательных напряжений в поперечном сечении трубы имеет вид.…

Ответ 6

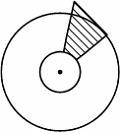
(т.к. , где– расстояние от центра тяжести поперечного сечения до точки, в которой определяется касательное напряжение.)

Вопрос 7

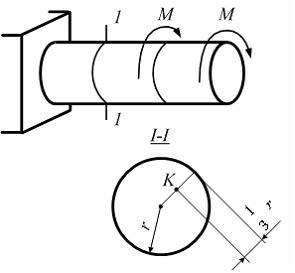
На рисунке показан стержень, работающий на кручение. Значение касательного напряжения в точке К поперечного сечения 1–1 равно …

Ответ 7

Касательное напряжение определим по формуле гдеПодставляя значенияв формулу касательного напряжения, получаем

Задание 11

Вопрос 1

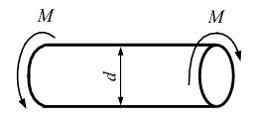
На рисунке показан стержень работающий на кручение. Известны величины , МПа. Минимально допускаемый размер стержня из расчета на прочность по допускаемым касательным напряжениям равен _____ см.

Ответ 1

8,6

Вопрос 2

Фактический коэффициент запаса по текучести круглого стержня из пластичного материала, работающего на кручение, определяется по формуле……(За критерий опасного состояния принять текучесть материала в самых напряженных точках).

Ответ 2

Вопрос 3

Условие прочности при кручении стержня круглого поперечного сечения с неизменным по длине диаметром имеет вид….

Ответ 3

Вопрос 4

Стержень круглого поперечного сечения диаметром работает на деформацию кручения. Касательное напряжение в точке, которая расположена на расстоянииот оси стержня, равно. Наибольшее касательное напряжение в данном поперечном сечении стержня равно…..

Ответ 4

(т.к. откуда на расстоянии)

Вопрос 5

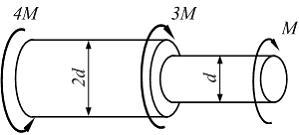
На рисунке показан ступенчатый вал, нагруженный моментами. Известны . Из расчета на прочность по допускаемым напряжениям минимально допускаемое значение параметраравно….

Ответ 5

(т.к. вал имеет два грузовых участка. На левом участке

На правом участке

Условие прочности

откуда

Вопрос 6

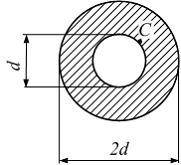
Труба испытывает деформацию кручение. Касательное напряжение в точке С поперечного сечения трубы равно . Предел текучести материала трубы при чистом сдвиге. Коэффициент запаса прочности равен….

Ответ 6

3

Максимальное касательное напряжение возникает в точках у внешней поверхности трубы, и его значение в два раза больше напряжения в точке С. Поэтому коэффициент запаса прочности.

Вопрос 7

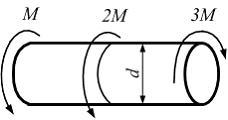
На рисунке показан вал, нагруженный  моментами. Известны величины: (предел текучести при чистом сдвиге). Исходя из понятия о точечной текучести, выражение для фактического коэффициента запаса по текучести в опасных точках имеет вид …

Ответ 7

Максимальные касательные напряжения действуют в поперечных сечениях правого грузового участка и равны Фактический коэффициент запаса по текучести

Задание 12

Вопрос 1

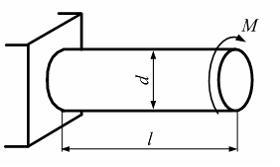
На рисунке показан стержень, работающий на кручение. Известны (допускаемый относительный угол закручивания). Из расчета на жесткость максимально допускаемоеМ равно….

Ответ 1

Вопрос 2

Условие жесткости при кручении стержня круглого поперечного сечения с неизменным по длине диаметром имеет вид….

Ответ 2

Вопрос 3

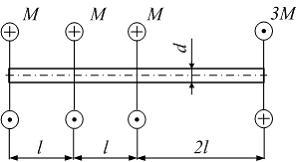
Стержень круглого сечения диаметром нагружен, как показано на рисунке. Максимальное значение относительного угла закручивания……

Модуль сдвига материала , моментаи длинызаданы.

Ответ 3

(т.к. , откуда)

Вопрос 4

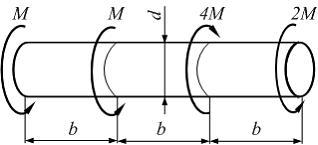
Из условия жесткости при заданных значениях иG, наименьший допускаемый диаметр вала равен.… (При решении принять .)

Ответ 4

Так как вал постоянного диаметра, условие жесткости имеет вид , где. Тогда.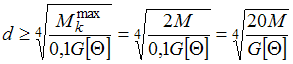

Вопрос 5

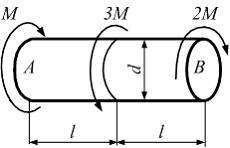
На рисунке показан стержень, работающий на кручение. Известны величины: (взаимный угол поворота концевых сечений в радианах). При заданном значениипараметр внешней нагрузкиМ равен …

Ответ 5

Стержень имеет два грузовых участка. Крутящий момент на левом участке М, на правом участке – - 2М. Знаки могут быть и обратные. Взаимный угол поворота концевых сечений откуда

Вопрос 6

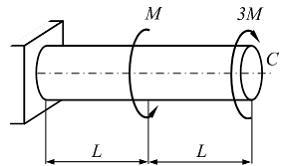
Схема нагружения стержня показана на рисунке. Длина L, жесткость поперечного сечения стержня на кручение ,– допускаемый угол поворота сеченияС – заданы. Из расчета на жесткость максимально допустимое значение параметра внешней нагрузки М равно …

Ответ 6

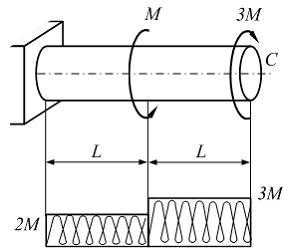Условие жесткости в данном случае имеет вид, где– действительный угол поворота поперечного сеченияС. Строим эпюру крутящего момента (смотри рисунок). Определяем действительный угол  поворота сеченияС.

Подставляем выражение действительного угла поворота в условие жесткости.откуда