Задание 3
Вопрос 1
В системе СИ напряжение измеряется…..
Ответ 1
Па, кПа, МПа
Вопрос 2
Для определения внутренних силовых факторов, действующих в сечении тела, используется….
Ответ 2
метод сечений
Вопрос 3
Полное и касательное
напряжение в точке сечения стержня
известны:
МПа,
МПа.
Нормальное напряжение в этой точке в
этой же точке сечения равно ____ МПа.
Ответ 3
4
(т.к.
)
Вопрос 4
Если известны нормальное и касательное напряжения в точке сечения, то полное напряжение в данной точке определяется по формуле …
Ответ 4
(т.к.
)
Вопрос 5
Проекции главного вектора и главного момента всех внутренних сил в данном сечении на три взаимно перпендикулярные оси, расположенные в этом же сечении по определенному правилу, называются….
Ответ 5
внутренними силовыми факторами
Вопрос 6
Внутренние силы в сечении стержня представляют, в общем случае,.…
Ответ 6
пространственную систему сил
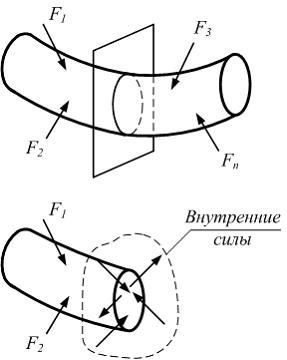
Внутренние силы можно показать, если разделить стержень сечением на две части и отбросить одну из них (см. рисунок). Внутренние силы в сечении представляют, в общем случае, пространственную систему сил.
Задание 4
Вопрос 1
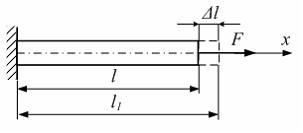
Первоначальная
длина стержня равна
.
После приложения силы
длина стержня стала
.
Величина
называется…..
Ответ 1
абсолютным удлинением
Вопрос 2
В результате
действия внешних сил на деформируемое
тело точка
заняла новое положение
.
Вектор
называется….
Ответ 2
полным перемещением
Вопрос 3
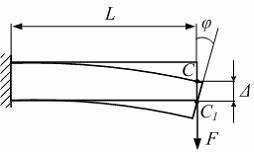
Угловым перемещением сечения (см. рис.) является величина…..
Ответ 3
Вопрос 4
Количественная мера изменения геометрических размеров в окрестности точки называется….
Ответ 4
линейной деформацией
Вопрос 5
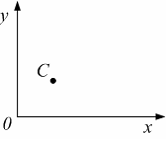
При нагружении
тела внешними силами точка С
перемещается в плоскости
.
Перемещение точки вдоль оси
равно 0,4мм,
а вдоль оси
- 0,3мм.
Полное перемещение точки равно ____ мм.
Ответ 5
0,5
(т.к
=
=0,5мм)
Вопрос 6
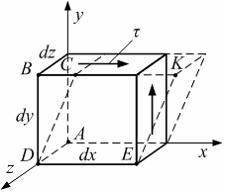
На рисунке показан элементарный параллелепипед и касательные напряжения на его гранях. Полагаем, что нижняя грань параллелепипеда жестко закреплена. Углом сдвига в точке А в плоскости xy является угол..
Ответ 6
BDC
Вопрос 7
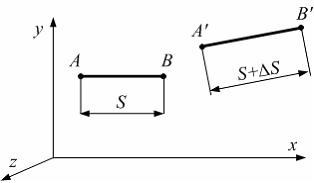Отрезок
АВ
длиной S
расположен параллельно оси х.
В процессе нагружения тела внешними
силами точки А
и В
перемещаются в положения
и
.
РасстояниеS
между точками изменяется
на величину
Линейная
деформация в точке А
по направлению оси x
равна …
Ответ 7
Линейная деформация в
точкеА по направлению оси x –
Задание 5
Вопрос 1
Из гипотезы плоских сечений следует, что вдали от мест нагружения, резкого изменения формы и размеров поперечного сечения нормальные напряжения при растяжении и - сжатии прямолинейных стержней распределяются по площади поперечного сечения…..
Ответ 1
равномерно
Вопрос 2
Для стержня, схеме
которого изображена на рисунке, продольная
сила
в сечении 2 – 2 будет…..
Ответ 2
сжимающей
Вопрос 3
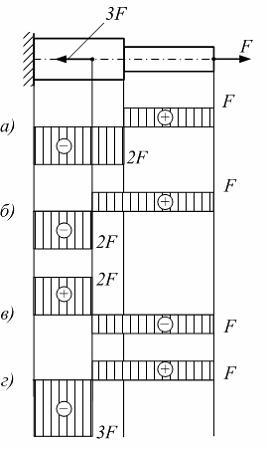
На рисунке показан
стержень нагруженный осевыми силами
и
.
Эпюра продольных сил показана на схеме….
Ответ 3
б
Вопрос 4
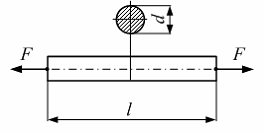
На рисунке показан
стержень, растянутый силами
.
Величины:
- заданы. Диаметр стержня изменится на
величину….
Ответ 4
(т.к. нормальное напряжение
Продольная деформация
Поперечная деформация
Изменение диаметра
)
Вопрос 5
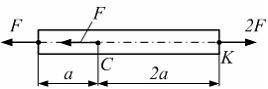
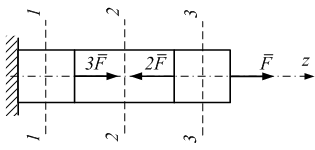
Стержень нагружен системой сил. Модуль упругости материала Е, площадь поперечного сечения А, размер а, значение силы F – заданы. Продольная линейная деформация на участке СК равна….
Ответ 5
Сделаем произвольное поперечное сечение на участке СКи рассмотрим равновесие правой отсеченной части.
Уравнение равновесия имеет вид
Откуда
Далее определяем нормальное напряжение
Из закона Гука
вычислим значение продольной линейной
деформации
Второй способ определения величины
.
Сначала определяем абсолютное удлинение
участкаСК
а затем продольную линейную деформацию
на этом участке