Глава 5
Методы дерандомизации
5.1Метод условных вероятностей
Оказывается, в некоторых случаях вероятностные алгоритмы могут быть «дерандомизированы», т. е. конвертированы в детерминированные алгоритмы. Один из общих методов, позволяющих сделать это, называется методом условных вероятностей.
Проблемы, связанные с дерандомизацией вероятностных алгоритмов при построении хороших целочисленных решений, в настоящее время находятся в центре внимания многих исследователей (см. [MR95]). После работы [Rag88], в которой вероятностным методом было доказано существование хороших целочисленных решений в задаче аппроксимации на решетке, появилось много работ, в которых та же техника использовалась для других задач. Эта техника получила название метода условных вероятностей.
При этом подходе эффективный детерминированный алгоритм нахождения искомого целочисленно-
203
204 Глава 5. МЕТОДЫ ДЕРАНДОМИЗАЦИИ
го вектора можно построить путем аппроксимации исходной задачи некоторым функционалом (обычно связанным с оценками вероятностей некоторых событий), и затем использовать покоординатное построение требуемого решения.
Опишем этот подход на примере следующей задачи: имеется величина X(x), где в булевом векторе x = (x1; : : : ; xn) компоненты являются независимыми случайными величинами, причем P fxi = 1g = pi,
P fxi = 0g = 1 pi.
Так, в задаче 20 «MAX-SAT» X(x1; : : : ; xn) равно числу невыполненных скобок в КНФ при вероятностном округлении.
Требуется найти любой булев вектор x^, для которого выполнено неравенство |
|
X(^x) E X: |
(5.1) |
Обозначим через X(xj x1 = d1; : : : ; xk = dk) новую случайную величину, которая получена из X фиксированием значений первых k булевых переменных.
Рассмотрим покомпонентную стратегию определения искомого вектора x^. Для определения его первой компоненты в x = (x1; : : : ; xn) вычисляем значения f0 E X(xj x1 = 0) и f1 E X(xj x1 = 1). Если f0 < f1, полагаем x1 = 0, иначе полагаем x1 = 1. При определенной таким образом первой компоненте
(обозначим ее d1) вычисляем значения функционала f0 |
E X(xj x1 = d1; x2 = 0) и f1 |
E X(xj x1 = |
d1; x2 = 1). |
|
|
Если f0 < f1, полагаем x2 = 0, иначе полагаем x2 = 1. |
|
|
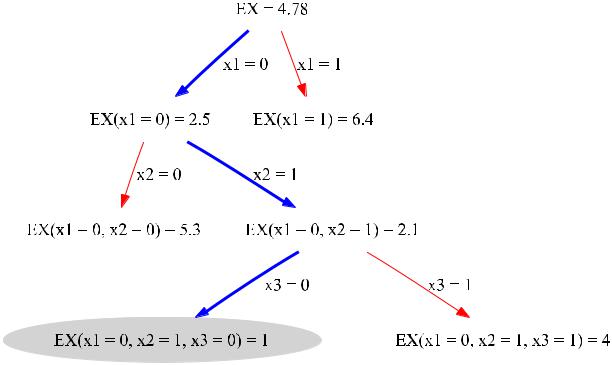
Фиксируем вторую координату (обозначая ее d2) и продолжаем описанный процесс до тех пор, пока не определится последняя компонента решения (см. рис. 5.1).
Почему найденный вектор будет удовлетворять (5.1)? Рассмотрим первый шаг алгоритма. Имеем
5.1. МЕТОД УСЛОВНЫХ ВЕРОЯТНОСТЕЙ
E X = Pfx1 = 1g E X(xj x1 = 1) + Pfx1 = 0g E X(xj x1 = p1 E X(xj x1 = 1) + (1p1 E X(xj x1 = d1) + (1
205
= 0) =
p1) E X(xj x1 = 0) p1) E X(xj x1 = d1) =
= (p1 + 1 p1) E X(xj x1 = d1) = E X(xj x1 = d1):
Продолжая эту цепочку неравенств для каждого шага, получаем на последнем n-м шаге
E X E X(xj x1 = d1; : : : ; xn = dn):
Но
E X(xj x1 = d1; : : : ; xn = dn) = X(d1; : : : ; dn);
и для построенного вектора x^ = (d1; : : : ; dn) выполнено неравенство (5.1).
Как оценить число шагов описанной процедуры? На каждой итерации вычисляются два условных математических ожидания (f0 и f1) и затем находится минимум этих величин. Если это делается за время O(L), то при общем числе итераций n получим оценку O(nL). Таким образом, изложенный общий метод позволяет осуществлять «дерандомизацию», если у нас есть эффективный алгоритм вычисления условных математических ожиданий (или условных вероятностей).
Теперь используем описанный выше метод условных вероятностей для задачи 20 «MAX-SAT». Математическое ожидание X равно сумме вероятностей невыполнения скобок:
∑j |
|
m |
|
E X = Pj; |
(5.2) |
=1 |
|
206 |
|
|
|
|
|
|
|
|
Глава 5. МЕТОДЫ ДЕРАНДОМИЗАЦИИ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.1: Дерандомизация на основе минимизации оценок математического ожидания
5.1. МЕТОД УСЛОВНЫХ ВЕРОЯТНОСТЕЙ |
207 |
|
|
||
Алгоритм 35 Дерандомизация вероятностного алгоритма 33 «вероятностный MAX-SAT» по методу услов- |
||
ных вероятностей |
|
|
Вход: Формулировка задачи 20 «MAX-SAT» в виде (4.1). |
|
|
Выход: |
(x1; : : : ; xm) — приближенное решение (4.1). |
|
(p1; |
: : : ; pn) решения линейной релаксации (4.2). |
|
for all i 2 f1::ng do
f0 = E X(xj xi = 0) {Вычисляется через (5.4)} f1 = E X(xj xi = 1) { и (5.2)}
if f0 < f1 then xi 0
else
xi 1 end if
end for return x
где вероятность невыполнения j-й дизъюнкции есть
|
< |
|
j |
|
j |
Pj = P |
> |
∑ |
∑ |
||
8 |
|
xi + |
|
(1 |
|
|
: |
|
C+ |
i C |
|
|
>i |
|
|||
|
|
2 |
|
2 |
|
9
>
=
xi) = 0> :
;
Для полученного вектора (d1; : : : ; dn) выполнено неравенство |
|
X(x1 = d1; : : : ; xn = dn) E X: |
(5.3) |
Из теоремы 18 следует, что E X (1/e)m, а из (5.3) вытекает, что X(x1 = d1; : : : ; xn = dn) (1/e)m.
208 |
Глава 5. МЕТОДЫ ДЕРАНДОМИЗАЦИИ |
Таким образом, мы находим допустимый 0–1 вектор x |
= (x1; : : : ; xn) с гарантированной верхней |
оценкой для целевой функции. |
|
Важный вопрос заключается в том, как эффективно вычислять условные математические ожидания. Предположим, значения первых k переменных уже определены и I0 — множество индексов переменных, значения которых равны 0, а I1 — множество индексов переменных, значения которых равны 1.
Нетрудно проверить, что если I0 \ Cj ≠ или I1 \ Cj+ ≠ , то Pj = 0. В противном случае
∏∏
Pj = |
(1 pi) |
pi: |
(5.4) |
|
i2Cj+nI0 |
i2Cj nI1 |
|
Запишем этот алгоритм более формально, в виде алгоритма 35 «MAX-SAT дерандомизация».
Упражнение 5.1.1. Покажите, что можно организовать вычисление f0 и f1 таким образом, что сложность алгоритма 35 «MAX-SAT дерандомизация» (кроме решения линейной релаксации) будет O(mn).
Упражнение 5.1.2. Честный попутчик в поезде предлагает вам сыграть в следующую игру, вариант классического «наперстка». т. е. есть три наперстка, шарик, ваша задача обнаружить шарик — тогда вы выигрываете, иначе — выигрывает сдающий.
Каждый раз на кон, вы и сдающий, ставите по 50 рублей. Сдающий тасует три наперстка, и прячет под одним из них шарик. Затем он предлагает вам выбрать наперсток. После того, как вы выбрали наперсток (пусть это будет наперсток «A»), вы можете открыть его, либо, заплатив еще 10 рублей, потребовать от сдающего, открыть пустой наперсток из двух оставшихся (пусть открытый будет «B»), после чего выбрать один из двух закрытых наперстков (т. е. «A» или «С»).
5.1. МЕТОД УСЛОВНЫХ ВЕРОЯТНОСТЕЙ |
209 |
Заметим, что сдающий и предметы честные (никаких «исчезающих» шариков и прочего мошенничества, наперсток для шарика выбирается совершенно случайно).
Какая стратегия оптимальна?
1.Не играть. Выигрыш — 0.
2.Выбрать наперсток «A» и открыть его.
3.Выбрать наперсток «A», «купить» открытие пустого наперстка «B», но выбрать наперсток «A».
4.Выбрать наперсток «A», «купить» открытие пустого наперстка «B», и выбрать наперсток «С».
Дорога длинная, играть можно много раз, правильная стратегия может привести к существенному обогащению, неправильная — к разорению…
Обоснуйте. Подсчитайте матожидание выигрыша для каждой из стратегий.
Рис. 5.2: Карта-памятка раздела 5.1.0