4.4. ВЕРОЯТНОСТНОЕ ОКРУГЛЕНИЕ |
|
191 |
Пусть Sk обозначает множество скобок, содержащих ровно k литералов, тогда: |
||
∑ ∑ |
(1 2 k) |
∑ ∑ |
n1 = |
(1 2 k)^zj: |
|
k Cj2Sk |
|
k Cj2Sk |
По лемме 22 имеем |
∑ ∑ kz^j: |
E n2 |
|
|
k Cj2Sk |
Следовательно,
|
n + n |
2 |
∑ ∑ |
(1 2 k) + |
k |
|
E |
1 |
|
z^j: |
|||
2 |
|
2 |
|
kCj2Sk
Простое вычисление показывает, что (1 2 k) + k 3/2 для всех натуральных k и, значит,
E |
n1 + n2 |
|
3 |
∑ ∑ |
|
3 |
∑ |
||
|
|
|
|
z^j = |
|
|
z^j: |
||
2 |
4 |
k Cj2Sk |
4 |
||||||
|
|
|
|
|
|
|
|
j |
|
4.4.2Максимальный разрез в графе
Задачи полуопределенного и векторного программирования. Использование эффективных алгоритмов для решений этих задач в вероятностном алгоритме решения задачи о максимальном разрезе в графе. Раздел основан на статье [GW95].
192 |
Глава 4. ВЕРОЯТНОСТНЫЕ АЛГОРИТМЫ И ИХ АНАЛИЗ |
Определение 4.4.2. Матрица X 2 Rn n является положительно полуопределенной если
8a 2 Rn; aTXa 0:
Обозначение: X 0.
Для симметрической X 2 Rn n следующее эквивалентно:
•X 0;
•X имеет неотрицательные собственные значения;
•X = V TV для некоторого V 2 Rm n, где m n.
Задача 21. «Полуопределенное программирование»².
∑
cijxij
i;j
∑
8k aijkxij
i;j
X = (xij)
8i; j xij
! max(min)
= bk;
0;
= xji:
²В англоязычной литературе SDP, semidefinite programming.
4.4. ВЕРОЯТНОСТНОЕ ОКРУГЛЕНИЕ |
193 |
Хотя задача 21 «SDP», несмотря на свою схожесть с линейным программированием, к нему не сводится, для нее существуют эффективные полиномиальные алгоритмы (модификации метода внутренней точки для ЛП), находящие приближенное решение с некоторой аддитивной ошибкой ϵ и временем, ограниченным полиномом по длине входа и O(log(1ϵ )).
Заметим, что, так как решение задачи 21 «SDP» может быть иррациональным числом, от численных методов точного (рационального) решения ждать и невозможно, хотя продолжаются попытки построить эффективный алгоритм нахождения точного решения алгебраическими методами.
Далее нам также пригодится эквивалентная формулировка задачи 21 «SDP» в виде задачи 22:
Задача 22. «Векторное программирование»³.
∑
cij(vi vj) ! max(min)
i;j
∑
8k |
aijk( |
v |
i |
v |
j) = bk; |
i;j
8i vi 2 Rn:
Эквивалентность задач 21 «SDP» и 22 «VP» следует из факторизации положительно полуопределенной матрицы X в виде X = V TV , т. е. xij = vi vj, где vi и vj — соответствующие колонки матрицы V .
Преобразование решения задачи 22 «VP» в решение задачи 21 «SDP» тривиально (одно матричное умножение), обратное не совсем — требуется разложение Холецкого , и это преобразование неоднозначно, но ничего принципиально сложного в этом нет — это классическая задача линейной алгебры.
³В англоязычной литературе VP, vector programming.Cholesky factoriza on или Cholesky decomposi on.
194 |
Глава 4. ВЕРОЯТНОСТНЫЕ АЛГОРИТМЫ И ИХ АНАЛИЗ |
Вероятностное округление при нахождении аппроксимации максимального разреза
Определение 4.4.3. Пусть есть неориентированный граф G = (V; E). Разрезом (сечением, cut) называется разбиение множества вершин V на непересекающиеся множества S и T . т. е. V = S [ T
и S \ T = .
Определение 4.4.4. Для неориентированного графа G = (V; E) и разреза (S; T ) ребро e = (v; t) счита-
ется пересекающим разрез, если v 2 S, а t 2 T .
Определение 4.4.5. Для графа G = (V; E) размером разреза (S; T ) считается число ребер, пересекающих этот разрез.
Если граф — взвешенный, т. е. каждому ребру e 2 E соответствует некоторый вес we, то разме-
ром разреза (S; T ) считается сумма весов ребер пересекающих этот разрез:
∑
R(S; T ) = |
we: |
|
e=(v;t)2E: v2S;t2T |
Задача 23. «Максимальный разрез/MAX-CUT».
Для взвешенного неориентированного графа G = (V; E) с весами we > 0 найти разрез (S; T ) с максимальным весом R(S; T ).
Упражнение 4.4.2. Докажите, что для простого, невзвешенного графа в задаче 23 «MAX-CUT» можно применить простую стратегию, дающую вероятностный 0:5-приближенный алгоритм: для каждой вершины с вероятностью 1/2 отнести ее к множеству S и с вероятностью 1/2 — к множеству T .
Упражнение 4.4.3. Студент предлагает для задачи 23 «MAX-CUT» приближенный алгоритм с точностью 12 : положить первую вершину в одну часть, последнюю — в другую, затем по-очереди добавлять оставшиеся вершины, к множеству, с которым у этой вершины меньше ребер-связей.
Прав ли студент?
4.4. ВЕРОЯТНОСТНОЕ ОКРУГЛЕНИЕ |
195 |
Наша цель — построить алгоритм с лучшими оценками точности приближения. Для этого сформулируем задачу 23 «MAX-CUT» как задачу целочисленного программирования.
Задача 24. «MAX-CUT(ЦП)»
G = (V; E) — входной граф, jV j = n;
W = (wij) — веса ребер, n n матрица. Для отсутствующего между vi и vj ребра — wij = 0;
yi — принадлежность вершины части разреза:
vi 2 S ! yi = 1, vi 2 T ! yi = 1. Ребро (vi; vj) 2 (S; T ) , yiyj = 1.
R(S; T ) — Вес разреза (S; T ). R(S; T ) = ∑ 1 yiyj wij:
Задача целочисленного квадратичного программирования:
∑ |
yiyj |
|
|
1 |
wij ! max |
||
ZЦП = |
|
2 |
|
i<j |
|
|
|
8i yi 2 f 1; 1g:
Видно, что постановка задачи 24 «MAX-CUT(ЦП)» внешне похожа на задачу 22 «VP», однако целочисленные ограничения в задаче 24 «MAX-CUT(ЦП)» делают ее существенно сложнее для решения. Рассмотрим следующую релаксацию задачи 24 «MAX-CUT(ЦП)».
196 |
|
|
|
|
Глава 4. |
ВЕРОЯТНОСТНЫЕ АЛГОРИТМЫ И ИХ АНАЛИЗ |
|||||||||||
Задача 25. «MAX-CUT(VP)» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
= |
1 vi |
vj |
w |
|
|
! max |
|||||||||
V P |
i<j |
2 |
ij |
||||||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
8i |
|
i |
|
i |
= |
1; |
||||||
|
|
|
|
|
v |
v |
|||||||||||
|
|
|
|
|
|
|
|
8i |
|
i |
2 |
Rn: |
|||||
|
|
|
|
|
|
|
|
v |
|||||||||
Эту задачу мы уже можем решать эффективно (см. выше), осталось разобраться, можно ли использовать решение задачи 25 «MAX-CUT(VP)» для нахождения решения (возможно приближенного) зада-
чи 24 «MAX-CUT(ЦП)».
Сначала заметим, что для оптимумов задач 24 «MAX-CUT(ЦП)» и 25 «MAX-CUT(VP)» выполняется
ZЦП ZV P :
Этот факт следует из того, что задача 25 «MAX-CUT(VP)» содержит задачу 24 «MAX-CUT(ЦП)» как частный случай.
Используя полученное решение задачи 25 «MAX-CUT(VP)» для вероятностного округления, получаем алгоритм 34 (концептуально аналогичный рассмотренному ранее алгоритму 33 «вероятностный MAXSAT»).
Нам понадобится небольшой технический факт.
Лемма 23.
min |
|
2 |
|
0:878: |
|
cos ) |
|||
0< (1 |
|
|||
4.4. ВЕРОЯТНОСТНОЕ ОКРУГЛЕНИЕ |
197 |
Доказательство. Рассмотрим график нашей функции на различных интервалах (Рис. 4.5). Функция имеет сингулярности в точках 0 и 2 , а на интервале (0; 2 ) функция выпуклая и имеет один минимум. Судя по построенным графикам, на интервале (0; 2 ) функция не меньше 0:878.
Чтобы убедиться в этом, найдем минимум (по равенству нулю производной) и вычислим значение функции в точке минимума. Воспользуемся системой компьютерной алгебры Maxima: возьмем производную и с помощью метода Ньютона найдем ее единственный нуль в интересующем нас интервале.
<load(”newton”);
<y:2*x/%pi/(1-cos(x));
<x0:newton(diff(y,x),3); > 2.331122370414422B0
<y(x0),numer;
> 0.87856720578485
Таким образом, можно даже утверждать, что
min |
|
2 |
> 0:8785672057848: |
|
|
||
0< (1 |
cos ) |
||
Теперь оценим качество алгоритма.
Теорема 20. Пусть (S ; T ) — оптимальный разрез для задачи 23 «MAX-CUT», тогда для математического ожидания величины разреза (S′; T ′), полученного вероятностным алгоритмом 34 «SDPокругление MAX-CUT», выполняется
E[R(S′; T ′)] 0:878 R(S ; T ):
198 |
Глава 4. ВЕРОЯТНОСТНЫЕ АЛГОРИТМЫ И ИХ АНАЛИЗ |
|
|
Рис. 4.5: График функции (1 |
2 |
|
cos ) |
|
4.4. ВЕРОЯТНОСТНОЕ ОКРУГЛЕНИЕ |
199 |
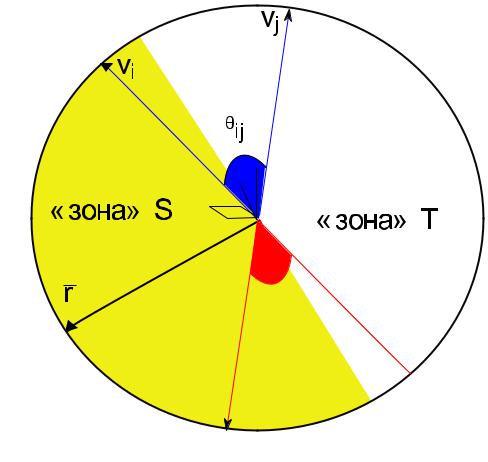
Рис. 4.6: Вектора в вероятностном округлении «MAX-CUT»
200 |
Глава 4. ВЕРОЯТНОСТНЫЕ АЛГОРИТМЫ И ИХ АНАЛИЗ |
Алгоритм 34 «SDP-округление MAX-CUT»
Вход: Формулировка задачи 23 «MAX-CUT» в виде задачи 24 «MAX-CUT(ЦП)» (v1; : : : ; vn) решения релаксации 25 «MAX-CUT(VP)»
случайно выбираем r из равномерного распределения векторов единичной длины
S T
for all i 2 f1::ng do if vi r 0 then
S S [ fig else
T T [ fig end if
end for
Выход: (S,T) — приближенное решение (23).
Доказательство. Возьмем некоторые i и j и соответствующие им векторы решения релаксации vi и vj. Затем оценим вероятность того, что при вероятностном округлении соответствующие вершины попадут в разные части разреза. Получим
|
|
P(yi ̸= yj) = P(yiyj = 1) = |
ij |
; |
|
|
||||||
|
|
|
|
|
|
|||||||
где ij — угол между векторами vi и vj. |
|
|
|
|
|
|
|
|
|
|||
Отсюда, используя определение математического ожидания: |
|
|
∑ |
|
|
|||||||
E |
∑ |
1 yiyj |
wij = |
∑ |
2 P(yi |
̸= yj) |
wij = |
ij |
wij: |
|||
i<j |
2 |
i<j |
2 |
|
i<j |
|
||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
С другой стороны, значение решения релаксации 25 «MAX-CUT(VP)» тоже можно выразить через углы ij:
ZV P = ∑ |
1 |
|
|
|
|
|
∑ |
1 cos |
|
|
v |
v |
|
|
ij |
|
|||||
|
i |
|
j |
wij = |
|
wij: |
||||
|
2 |
|
|
2 |
|
|||||
i<j |
i<j |
4.4. ВЕРОЯТНОСТНОЕ ОКРУГЛЕНИЕ |
201 |
Теперь оценим минимальное качество решения, используя лемму 23: |
|
|
|
||||||||||||
|
|
|
|
∑ |
|
2 |
|
|
|
|
|
|
|
|
|
E[R(S′; T ′)] |
|
E[R(S′; T ′)] |
|
|
|
ij |
wij |
|
|
|
2 |
|
|
||
R(S ; T ) |
|
|
= |
∑ |
|
1 |
cos ij |
|
|
min |
|
cos ) |
|
0:878: |
|
ZV P |
|
|
wij |
0< (1 |
|
||||||||||
|
|
i<j |
|
|
|
||||||||||
202 |
|
|
Глава 4. ВЕРОЯТНОСТНЫЕ АЛГОРИТМЫ И ИХ АНАЛИЗ |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.7: Карта-памятка раздела 4.4.2