beskin

202

энергию δǫ, заключенную в единице объема в диапазоне частот между ω и ω + δω. Определяя теперь эту энергию как δǫ = w(ω, T )δω, получаем окончательно для плотности энергии w(ω, T ), которая приходится на интервал частот δω:

Зная же плотность излучения w(ω, T ) (размерность эрг см−3 Гц−1), нетрудно опреде-

лить и спектральную плотность потока P (размерность эрг см−2 c−1Гц−1). Если бы все

фотоны распространялись перпендикулярно элементу площади δS, то тогда можно было бы записать просто P = cw. Действительно, через площадку δS за время δt прошла бы вся энергия, заключенная в объеме δScδt (фотоны распространяются со скоростью света).

В случае же изотропного излучения мы должны учесть то, что фотоны, распространяющийся под углом θ к поверхности δS, будут фактически приходить из объема δScδt cos θ

и, кроме того, половина фотонов вообще будет распространяться в противоположную сторону. Поэтому в этом случае (проверьте!) P = (1/4)cw. В итоге, получаем

Как уже отмечалось, это соотношение с хорошей точностью описывает излучение абсолютно черного тела при hω¯ T .

Формула (302) является одной из основных расчетных формул в наблюдательной радиоастрономии. Действительно, если из наблюдений известна величина P(ω), то тогда

мы можем определить величину

которая называется яркостной температурой источника на частоте ω. Понятно, что величина Tb будет совпадать с реальной температурой излучающей среды лишь в том случае,

если излучение имеет тепловую природу и если частота наблюдения достаточно мала, так что мы можем пользоваться приближением Релея-Джинса. Для источников же, у которых Tb составляет 1015–1020 K, можно с уверенностью сказать, что их излучение не

связано с тепловыми процессами.

203

8.3Формула Планка

Для вывода формулы Планка (20) нам потребуется результат, основанный на полной версии принципа равнораспределения энергии по степеням свободы. А именно распределение Гиббса одно из ключевых соотношений статистической физики. Как мы уже отмечали выше, в Приложении 8.1 был рассмотрен случай, когда все состояния имеют одинаковую энергию. Если же различные состояния имеют разную энергию, то уже интуитивно ясно, что частицам будет выгодно занимать нижние энергетические уровни. Тем не менее, принцип равнораспределения может быть сформулирован и этом случае.

Дело в том, что физически правильной постановкой задачи будет вопрос о том, каким будет распредение N частиц по уровням энергии εn при заданной величине полной

энергии

n=1

Здесь Nn число частиц, занимающих энергетический уровень εn, а K количество

различных уровней энергии. При этом заданным должно быть еще и полное число частиц

которая обобщает соотношение (293). При этом величина G (т.е. статистический вес) показывает, сколькими способами можно разместить N1 частиц в первой ячейке, N2 частиц

во второй, и т.д. при выполнении условий (304) и (305). Здесь и используется фундаментальное предположение о том, что все состояния с данной энергией равновероятны.

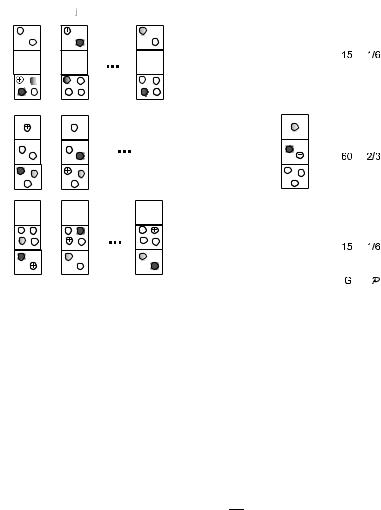
На Рис. 32 для иллюстрации показано, как можно разместить шесть одинаковых молекул в трех ячейках, имеющих энергии 0, ε и 2ε, так, чтобы полная энергия системы составляла 4ε. Таких комбинаций, как мы видим, всего три. Но количество вариантов,

которыми можно расположить молекулы (т.е. статистические веса соответствующих состояний) при этом различны.

204

.

Рис. 32: Различные варианты размещения шести одинаковых молекул в трех ячейках, имеющих энергии 0, ε и 2ε, так, чтобы полная энергия системы составляла 4ε. Показаны также статистические веса G и вероятности выпадения соответстенных состояний

Используя теперь, как и в Приложении 8.1, формулу Муавра-Стирлинга (295), а также (что очень важно!) соотношения (304) и (305), можно показать, что

где N0 некоторая постоянная. Это и есть соотношение, найденное Дж. Гиббсом (1839-

1903) и носящее его имя. Как и в случае распределения Гаусса (8), оно получается в пределе очень больших значений N . Действительно, при малых N , как показано на Рис. 32,

вероятности различных состояний хотя и отличаются друг от друга, но все же могут совпадать по порядку величины. При больших же N , как и для распределения Гаусса,

практически реализуется лишь наиболее вероятное состояние. Впрочем, и на нашем, чрезвычайно упрощенном примере видно, что наиболее вероятным является состояние, при котором числа заполнения энергетических уровней плавно уменьшаются с увеличением их энергий.

Здесь, правда, неообходимо отметить еще одно обстоятельство. На первый взгляд, непонятно, в каком месте в наших рассуждениях могла возникнуть температура T . Дело

206

K фотонов может быть записана в виде Khω¯ . Как легко проверить, точная формула (94), содержащая фактор (K + 1/2), приводит к тем же результатам.

Итак, нам вновь нужно посчитать энергию, которую содержат фотоны в диапазоне частот от ω до ω + δω. При этом, как и в пределе Релея-Джинса, число состояний в элементе объема δV будет задаваться формулой δN = (ω2/π2c3)δV δω (299). Отличие будет состоять лишь в том, что энергия разных колебаний будет отличаться от T .

Действительно, давайте применим общий принцип, найденный Гиббсом, для фотонов, имеющих одинаковую энергию hω¯ . Поскольку при эквидистантности уровней осцилляторов энергии излученных фотонов могут принимать лишь значения Khω¯ , где K целое

число, получаем с учетом общего соотношения (307) для вероятности фотону иметь энергию Khω¯

K=0

Поскольку же сумма всех вероятностей должна быть равна единице, получаем оконча-

K=0

есть т.н. статистическая сумма, играющая ключевую роль в статистической физике. В

208

стороны, ускорение электрона можно записать как r¨ = e2/a2Bme. В результате, имеем для оценки времени жизни τ

Конечно, для количественной оценки величины τ можно было бы сразу подставить

числовые значения заряда и массы электрона, радиуса Бора и скорости света. Однако иногда бывает удобнее несколько перегруппировать члены, объединив их в известные комбинации. Действительно, воспользовавшись определением радиуса Бора aB (119), по-

Как мы видим, для оценки времени жизни нам нужно знать лишь значения постоянной тонкой структуры α = e2/hc¯ ≈ 1/137, радиуса Бора aB и скорости света c. Имеем в итоге

где ωc есть частота вращения, а re классический радиус электрона. Эта формула оказы-

вается более универсальной, поскольку она справедлива для любого кругового движения с частотой ωc.

8.5Cоотношение неопределенностей точная формулировка

Внимательный читатель должен был бы обратить внимание на то, что соотношение

неопределенностей Гейзенберга x px ≥ h/¯ 2 (60) (и, соответственно, соотношение для

волн x kx ≥ 1/2 (59)) безусловно, требуют уточнения. Действительно, справа стоит

четкая граница h/¯ 2 (или 1/2). Следовательно, и стоящие слева величины x и kx тре-

буют точного определения.

Как уже говорилось, значения x и kx должны быть определены как среднеквадратичные отклонения от их средних значений x0 и k0. Формальное определение x для

209

произвольной волны A = A(x), достаточно быстро спадающей при x → −∞ и x → ∞,

Эти соотношения на самом деле суть просто обобщения определения среднего арифметического для непрерывно распределенных величин.

Здесь нужно отметить два обстоятельства. Прежде всего, как мы уже отмечали, ”мерой” распределения должен быть именно квадрат амплитуды волны. В противном случае для знакопеременного сигнала можно получить совершенно неверный результат. В частности, для любого сигнала, описываемого нечетной функцией A(−x) = −A(x), вообще

невозможно определить величины, которые должны были стоять в знаменателях (324)– (325). Появление же модуля функции A(x) позволяет использовать это соотношение и

для комплексных сигналов. При этом, как мы видим, в определениях (324)–(325) вместо

A(x) может быть использована и волновая функция ψ(x).

Что же касается величин kx и px, то для них определние среднеквадратичных

отклонений на первый взгляд должно проводиться по совершенно различным формулам.

Здесь k0 среднее значение kx, определяемое по аналогии с (325). С другой стороны, по

канонам квантовой механики квадрат импульса, благодаря соотношению (92), следует

Однако, как можно показать, оба этих определения будут приводить к одному и тому же значению px = h¯ kx.

В качестве примера рассмотрим пространственную волну A(x), задаваемую уже зна-

Коэффициент перед экспонентой выбран таким образом, чтобы знаменатели в соотношениях (324)–(325) были равны единице. Поскольку же ”весом” в интеграле (324) будет квадрат амплитуды волны A(x), т.е. величина e−x2/x20 , не содержащая двойку в знамена-

теле экспоненты, то, как легко проверить,

С другой стороны, замечательное свойство функции Гаусса g(x) e−x2/2 состоит в том, что она совпадает по форме со своим преобразованием Фурье (326): gˆ(k) e−k2/2. Поэто-

и, следовательно, x px = 1/2. Читателю самому предоставляется возможность убе-

диться, что формула (328) приводит к тому же результату. Таким образом, можно сделать вывод, что для гауссова профиля реализуется наименьшее из значений, разрешенных соотношением неопределенностей Гейзенберга.

34Мы для порядка поставили звездочку, которая означает, что для комплексных волновых функций

здесь должна стоять величина, комплексно сопряженная к ψ(x).