Электродинамика. Программа. 2 семестр

5-1) В начале координат покоится точечный диполь p1 = (p1; 0; 0). Â òî÷-

êå (x; 0; 0) находится другой точечный диполь p2 = (p2; 0; 0). Найти модуль

и направления сил взаимодействия диполей. Найти также модуль и направления сил взаимодействия в случае, когда второй диполь находится в точке

(0; y; 0).

5-2) В пространстве имеется произвольная система проводников с фиксированными зарядами или потенциалами. Доказать, что поле в пространстве между проводниками формируется однозначно, соответственно заряд однозначно распределяется по поверхностям проводников. (Теорема единственности). (Указание: общий случай свести к частному, когда заряды или потенциалы проводников равны нулю, и записать энергию системы двумя способами).

5-3) Незаряженный проводящий шар радиуса R = 4см, разрезанный попо-

лам, находится во внешнем однородном поле E0 = 300Â=см, перпендикуляр-

ном к плоскости разреза. Найти силы, действующие на полушария, рассмотрев два случая: (1) шар сначала поместили в электрическое поле, а потом разрезали; (2) шар сначала разрезали, а потом поместили в электрическое поле. Притягиваются полушария или отталкиваются?

Семинар 6.

6-1) В пространстве хаотично распределены проводящие шарики радиуса r. Концентрация n шариков такова, что nr3 1. Найти диэлектрическую

проницаемость " этой среды. Решить также задачу для случая плотной среды nr3 1. (Указание: мысленно выделить из среды большой шар радиуса R r и рассмотреть действие на него оставшейся части среды).

6-2) Длинный тонкий цилиндр (длина 2h, радиус поперечного сечения r) вырезан из вещества с вмороженной однородной поляризацией P, направленной вдоль оси цилиндра. Найти напряж¼нности электрического поля в центре торца (EA) и на боковой стенке в середине между торцами ( EB). Êà- чественно нарисовать силовые линии полей E è D внутри и вне цилиндра.

6-3) Пластина из сегнетоэлектрика ( " = 200) имеет толщину, равную за-

зору между обкладками плоского конденсатора. Площадь каждой обкладки конденсатора S1 = 1ì2. Площадь боковой грани пластины S2 < S1. Какова

должна быть площадь S2 для того, чтобы в объ¼ме пластины индукция электрического поля сделалась в N = 40 раз больше, чем было в конденсаторе

до введения пластины? Конденсатор изолирован.

Семинар 7.

7-1) Заземление концов телеграфной линии осуществлено посредством очень глубоко зарытых в землю металлических шаров радиусами r1 è r2. Удельная проводимость почвы вблизи них равна 1 è 2. Найти сопротивление R земли

11

между шарами.

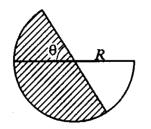
7-2) Конденсатор переменной ¼мкости состоит из двух неподвижных металлических пластин (обкладок), расположенных на расстоянии d äðóã îò

друга, и подвижной диэлектрической пластины с проницаемостью ", которая

может поворачиваться и входить в зазор между металлическими пластинами (см. рисунок). Заряженные обкладки конденсатора могут быть подсоедине-

ны к батарее с э.д.с. V или отсоединены от батареи (в любом случае разность потенциалов между обкладками принимается равной V ). Пренебрегая краевыми эффектами, найти момент M электрических сил, действующих на диэлектрическую пластину, когда она пов¼рнута на угол относительно пла-

стин конденсатора (как в случае подключ¼нной, так и в случае отлюч¼нной батареи). Куда направлен этот момент? Все пластины имеют форму полукру-

га радиуса R, прич¼м зазоры между диэлектрической пластиной и обкладками конденсатора пренебрежимо малы по сравнению с d.

К задаче 7-2)

7-3) Пространство между обкладками плоского конденсатора заполнено неоднородным, слоистым (слои параллельны обкладкам конденсатора) диэлектриком, обладающим слабой электропроводностью. Диэлектрическая про-

ницаемость и удельная проводимость диэлектрика плавно изменяются от зна- чений "1 = 4, 1 = 10 9Îì 1ñì 1 на одной обкладке до значений "2 = 3,

2 = 10 12Îì 1ñì 1 на другой. Конденсатор подключ¼н к батарее с посто-

янной э.д.с. Найти величину и знак суммарного свободного заряда, который возникает в диэлектрике, когда в цепи устанавливается постоянный электри- ческий ток I = 10 7А, текущий через диэлектрик от обкладки 1 к обкладке

2.

Семинар 8.

8-1) По проводнику, имеющему форму гофрированной окружности (см. рисунок), теч¼т ток I = 10А. Форма проводника описывается уравнением

1=r = 1=a + b cos (m'), ãäå a = 50ñì, m целое число и b постоянная. Найти магнитное поле B в центре O проводника.

12

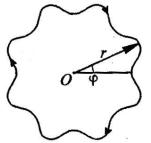
К задаче 8-1)

8-2) Соленоид состоит из N витков, равномерно намотанных на длине L на цилиндр диаметром D. По виткам теч¼т ток I. Найти модуль и направление индукции магнитного поля B на оси соленоида в точке A на расстоянии x от его центра, суммируя магнитные поля от отдельных витков соленоида. Показать, что эта индукция может быть выражена через углы и , где 2 è 2 это углы, под которыми из точки A видны диаметры торцов. Найти такой способ вычисления магнитного поля в точке A, чтобы ответ, выраженный через углы и , получался сам собой.

8-3) Заряженный шарик радиусом R равномерно вращается вокруг своего диаметра с угловой скоростью !. Заряд шарика равен q. Найти магнитный момент m шарика, если заряд равномерно распредел¼н: (1) по поверхности

шарика; (2) по объ¼му шарика.

Семинар 9.

9-1) Длинный тонкий цилиндр (длина 2h, радиус поперечного сечения r) вырезан из вещества с однородной постоянной намагниченностью M, направленной вдоль оси цилиндра. Найти индукцию магнитного поля в центре торца (BA) и на боковой стенке в середине между торцами ( BC). Нарисовать (качественно) силовые линии полей B è H внутри и вне цилиндра.

9-2) Бесконечная плоская пластина изготовлена из однородного намагни- ченного ферромагнетика, прич¼м вектора намагниченности M параллелен

плоскости пластины. Найти поля B è H внутри и вне пластины.

9-3) Тонкий сердечник тороидальной катушки длиной L сделан из ферромагнитного материала. Минимальная напряж¼нность магнитного поля, при которой намагниченность материала достигает насыщения ( M = Míàñ), ðàâ-

I0, который должен течь по обмотке для того, чтобы намагниченность сердечника достигла насыщения. Какой воздушный зазор x должен быть сделан в сердечнике для того, чтобы не

возникало насыщение намагниченности, если по обмотке теч¼т ток I > I0? Число витков равно N.

Семинар 10.

13

10-1) В бетатроне (ускорителе электронов до релятивистских энергий) роль ускоряющего напряжения играет э.д.с. индукции, возбуждаемая изменением магнитного потока, пронизывающего орбиту электронов. При этом электроны движутся по окружности постоянного радиуса. Показать, что это возмож-

но, только если в каждый момент времени t выполняется определ¼нное соотношение между средним магнитным полем < B(t) >, пронизывающим орбиту электрона, и магнитным полем B(t) на орбите электрона (это соотношение

называют бетатронным условием). Рассмотреть в качестве примера случай, когда магнитное поле зависит от r è t по закону: B(r; t) = (B0 r2)f(t),

ãäå r расстояние от оси бетатрона, B0 и положительные постоянные,

à f(t) растущая функция времени t. Найти радиус r0 орбиты, по которой движутся ускоряемые электроны.

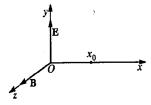
10-2) В скрещенных постоянных и однородных полях E è B, в таких что E ? B è E B, из некоторой точки x0 íà îñè x разлетаются нерелятивистские электроны, скорости v которых лежат в плоскости (x; y) (см. рисунок). Показать, что через некоторое время T все электроны соберутся в одну точку. Найти положение этой точки и время T .

К задаче 10-2)

10-3) В однородное магнитное поле с индукцией B помещена металличе- ская лента шириной L и толщиной b так, что плоскость ленты перпендикулярна индукции B. По ленте пропускают ток I. Найти разность потенциалов V , возникающую между краями ленты (т.е. на расстоянии L), если концентарация свободных электронов в металле ленты равна n. Возникновение разности потенциалов V называют эффектом Холла, а отношение R = V=I сопротивлением Холла.

ЗАДАНИЕ

Задание к семинару 1.

1-1) По двум длинным прямым проводам, расположенным параллельно на расстоянии d друг от друга, равномерно распределены разноим¼нные заряды

с линейной плотностью + и . Найти напряж¼нность электрического поля в точке, находящейся на расстоянии h от плоскости, в которой лежат провода,

14

и равноудал¼нной от проводов. Рассмотреть предел d ! 0 è ! 1, åñëè d = { = const.

1-2) Диск радиусом R заряжен равномерно с поверхностной плотностью. Найти напряж¼нность электрического поля в точке, которая находится на расстоянии h от диска на перпендикуляре, проходящем через центр диска. Рассмотреть также предельные случаи R h è R h.

1-3) В равномерно заряженном бесконечном плоском слое толщины d с объ¼мной плотностью зарядов вырезана сферическая полость. Центр полости находится в середине между поверхностями слоя, диаметр полости меньше толщины слоя d. Найти напряж¼нность электрического поля в полости (зависимости Ex(x; y; z), Ey(x; y; z) è Ez(x; y; z), если начало координат помещено в центр полости, а ось x перпендикулярна слою).

Задание к семинару 2.

2-1) Найти зависимость потенциала электростатического поля от расстояния до оси бесконечного равномерно заряженного цилиндра радиуса R. Îáú-

¼мная плотность зарядов в цилиндре равна . Принять, что потенциал на оси цилиндра равен 0. Нарисовать график полученной зависимости.

2-2) Длинная проводящая проволока радиуса поперечного сечения r помещена в однородное электрическое поле E0, направленное вдоль оси z попер¼к оси проволоки (оси x). Найти плотность (') распределения заряда по поверхности проволоки (' это азимутальный угол между направлением на точку поверхности из точки на оси проволоки и осью z).

2-3) Металлический шар радиусом R1, несущий заряд Q, находится внутри сферического металлического слоя с внутренним радиусом R2 и внешним

радиусом R3 (центры шара и слоя совпадают). Найти потенциал и напря-

ж¼нность электрического поля в зависимости от расстояния от центра шара. Построить графики полученных зависимостей. Чему равны потенциалы проводников? Что изменится, если проводящий сферический слой заземлить? Нарисовать графики соответствующих зависимостей для этого нового слу- чая.

Задание к семинару 3.

3-1) Вычислить напряж¼нности электрического поля равномерно заряженных: (1) шара радиуса R и (2) бесконечной пластины толщины h, используя теорему Гаусса в дифференциальной форме. В обоих случаях объ¼мная плотность зарядов равна .

3-2) В начале координат расположен электрический диполь p, направленный вдоль оси x. Вычислить поток электрического поля этого диполя через круг радиуса R, перпендикулярный оси x, с центром на оси x в точке x0.

15

Обсудить пределы R ! 0 è R ! 1.

3-3) Заряд q находится на расстоянии R=2 от центра тонкостенной металли- ческой изолированной сферы радиуса R. Заряд сферы равен Q. Найти силу,

действующую на заряд, а также поверхностную плотность зарядов на сфере в самой ближней к заряду и самой дальней от заряда точках.

Задание к семинару 4.

4-1) Вычислить дивергенцию и ротор поля E(x; y; z) = (2y; 2x + 3z; 3y). Является ли это поле потенциальным? Если да, то найти его потенциал '(x; y; z). Проверить, что линейный интеграл от E между произвольными

точками A è B совпадает с убылью потенциала 'A 'B.

4-2) На плоскости задано поле E(x; y) = (axy; b(x2 y2)), ãäå a è b постоянные. При каком соотношении между постоянными a è b ïîëå E является потенциальным? Для найденных a è b определить потенциал '(x; y), а также плотность заряда (x; y), формирующего это поле.

4-3) Вычислить дивергенцию и ротор поля:

потенциальным? Если да, то определить потенциал '(x; y), а также плотность заряда (x; y), формирующего

ýòî ïîëå.

Задание к семинару 5.

5-1) Внутри равномерно заряженной сферы радиуса R и постоянного заряда Q находится проводящая сфера радиуса r < R и заряда q (центры сфер совпадают). Заряд q может меняться. Найти энергию W системы в зависимости от заряда q. При каком q эта энергия минимальна? Какой заряд

установится на внутренней сфере, если е¼ заземлить?

5-2) Предположим, что энергия покоя электрона E0 = mc2 åñòü íå ÷òî èíîå,

как энергия электрического поля покоящегося электрона. Считая электрон сферическим, найти радиус электрона при двух предположениях: (1) весь заряд электрона распредел¼н равномерно по его поверхности; (2) весь заряд электрона равномерно распредел¼н по его объ¼му. Полученные ответы выражаются через одну и ту же комбинацию мировых констант: элементарного

заряда e, массы электрона m и скорости света c. Саму эту комбинацию r0 íà- зывают классическим радиусом электрона. Вычислить r0, åñëè e = 4:8 10 10 ÑÃÑÝq, m = 0:91 10 27 ã è c = 3 1010 см/с. В случае, когда заряд распредел¼н по поверхности, вычислить также давление (в атм) изнутри на поверхность

16

электрона.

5-3) В безграничном плоском слое толщиной 2l объ¼мная плотность заряда

изменяется по закону = 0x=l ( l < x < l), ãäå x ось, перпендикулярная слою (нуль находится в середине слоя). В слое имеется тонкий канал вдоль оси x, в который помещ¼н точечный диполь с массой m и дипольным

моментом p, направленным вдоль канала. Вычислить частоту малых колебаний диполя вдоль оси x (направление момента p в процессе колебаний не

меняется).

Задание к семинару 6.

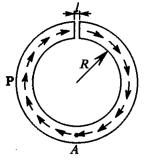
6-1) Диэлектрический образец с замороженной поляризацией P имеет фор-

му полого цилиндра с разрезом. На рисунке показано сечение этого цилиндра и направление вектора поляризации. Толщина стенки цилиндра h R, ãäå

R радиус цилиндра; ширина разреза l h. Найти электрическое поле E и индукцию D в точке A и в центре разреза.

К задаче 6-1)

6-2) Диэлектрическая пластина толщины h с замороженной однородной поляризацией P помещена внутрь плоского конденсатора параллельно его обкладкам (площади боковых граней пластины равны площадям обкладок) и не примыкает к ним. Расстояние между обкладками равно d (d > h). Вектор P перпендикулярен боковым граням пластины и обкладкам конденсатора. Обкладки соединены проводом. Найти напряж¼нность Ex(x) и индукцию Dx(x) электрического поля внутри вне пластины (ось x перпендикулярна пластине и направлена вдоль вектора P). Нарисовать графики этих функций.

6-3) Напряж¼нность электрического поля в вакууме вблизи плоской поверхности однородного диэлектрика с проницаемостью " равна E0 и состав- ляет угол с нормалью n к поверхности диэлектрика. Считая поля внутри

и вне диэлектрика однородными, найти: (1) потоки E è D векторов E è D соответственно через поверхность сферы радиуса R, центр которой лежит на поверхности диэлектрика; (2) циркуляции CE è CD векторов E è D соответственно по прямоугольному контуру со сторонами l1 è l2 (ñì. ðèñ.).

17

К задаче 6-3)

Задание к семинару 7.

7-1) Плоский конденсатор с квадратными обкладками (расстояние между обкладками d, площадь каждой обкладки S) заряжен до разности потенциа-

ëîâ V0. В конденсатор вдвигают до половины пластину диэлектрика с проницаемостью ". Толщина пластины равна d. Найдите силу, с которой пластина

втягивается в конденсатор, если (1) после зарядки (и до вставки пластины) конденсатор был отключ¼н от батареи; (2) после зарядки конденсатор остался

подключ¼нным к батарее с э.д.с. V0.

7-2) Две половинки сферического конденсатора заполнены диэлектриками с проницаемостями "1 è "2 (схема представлена на рисунке). Найти силу, действующую на внутреннюю сферу. Заряд конденсатора Q, радиус внутренней

сферы R.

К задаче 7-2)

7-3) Пусть C это ¼мкость системы из двух проводников произвольной

формы, разнес¼нных на некоторое расстояние друг от друга в вакууме. Заполним вс¼ пространство между проводниками однородной проводящей средой с

удельным сопротивлением . Показать, что сопротивление R среды току, текущему между проводниками, равно =(4 C) (в системе СГСЭ). Какой будет

ответ, если использовать единицы СИ?

Задание к семинару 8.

8-1) По проводнику, имеющему форму эллипса, теч¼т постоянный ток I = 10 А. Большая и малая полуоси эллипса равны соответственно a = 50 ñì,

18

b = 30 см. Найти модуль и направление индукции магнитного поля B в фокусе эллипса. Уравнение эллипса в полярной системе коордèíàò èìååò âèä:

p

r(') = p=(1 + e cos(')), ãäå p = b2=a параметр, а e = 1 b2=a2 < 1 эксцентриситет; начало координат совпадает с одним из фокусов эллипса.

8-2) По оси полого длинного цилиндра ( R1 è R2 радиусы внутренней и внешней поверхностей цилиндра) натянута заряженная нить, на 1 см длины которой приходится заряд { = 1 ÑÃÑÝq. Цилиндр вращается вокруг своей оси с угловой скоростью = 1000 ñ 1 (схема представлена на рисунке). Най-

ти индукцию магнитного поля B(r) вдали от его торцов в полости цилиндра, r < R1, в материале цилиндра, R1 < r < R2, и вне цилиндра, r > R2 (íà расстояниях r от оси, небольших по сравнению с длиной цилиндра), в двух случаях: (1) цилиндр металлический, немагнитный; (2) цилиндр диэлектри- ческий (" = 3). Всеми эффектами, связанными с центробежными силами, можно пренебречь.

К задаче 8-2)

8-3) Равномерно заряженная с линейной плотностью квадратная рамка со стороной l вращается с угловой скоростью ! вокруг одной из сторон. Найти

магнитный момент рамки m.

Задание к семинару 9.

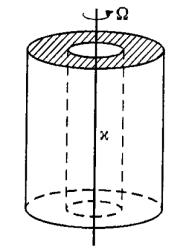
9-1) Постоянный магнит и соленоид выполнены в виде одинаковых цилиндров (с одинаковыми высотами и поперечными сечениями). Намагниченность

M вещества постоянного магнита постоянна и направлена вдоль оси цилиндра. Какой ток нужно пустить по соленоиду с плотностью намотки n для того, чтобы индукция B в постоянном магните и соленоиде была одинаковой? Нарисовать (качественно) силовые линии полей B è H для постоянного магнита и соленоида.

19

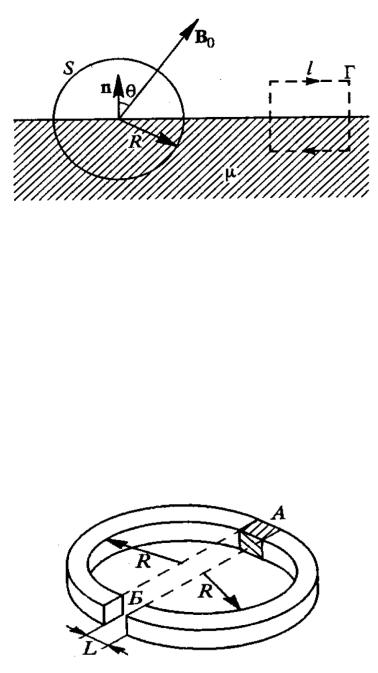
9-2) Индукция магнитного поля в вакууме вблизи плоской поверхности магнетика с проницаемостью равна B0, прич¼м вектор B0 составляет уголс нормалью n к поверхности (см. рисунок). Найти: (1) потоки B è H векторов B è H через поверхность сферы S радиусом R, центр которой ле-

жит на поверхности магнетика; (2) циркуляции CB è CH векторов B è H по квадратному контуру со стороной h (см. рисунок).

К задаче 9-2)

9-3) Сердечник, выполненный из мягкого железа с магнитной проницаемостью 1 в виде тонкого кольца радиуса R, разрезан по диаметру (см.

рисунок). Половинки сердечника раздвинуты на расстояние L R. Один из зазоров (А) замкнут небольшим постоянным магнитом в виде бруска длины L с намагниченностью M, направленной вдоль оси цилиндра (поперечное сечение магнита совпадает с поперечным сечением сердечника). Найти напряж¼нность H и индукцию B магнитного поля в другом зазоре (Б). Рассеянием магнитного потока пренебречь.

К задаче 9-3)

Задание к семинару 10.

10-1) В длинном воздушном соленоиде с радиусом намотки R и плотно-

20