Билеты по теории вероятности
.docx|
1 - Определение случайного события, операции над событиями, совместные(несовместные) события Ω = {ω} – множество элементарных исходов. А ⊂ Ω [А - случайное событие] А + В – сумма событий[произошло хотя бы одно] А * В – произведение событий [оба произошли] А и В несовместные события, если. А* В = Ø А–В – разность событий [А да, В нет] Ā = Ω - А – противоположное событие [Ā проиходит когда А не происходит] События А1, А2, …,Аn называются попарно несовместимыми, если Аi * Аj = Ø, i ≠ j События
А1,
А2,
.., Аn
несовместные
в совокупности,если А1
*
А2
*…*
Аn
=
|
2 Свойства операций
Свойства противоположного события
|
5 Определение условной вероятности и ее свойства Р(А/В)= !Если
А не зависит от В , то В не зависит от
А, А не зависит от Свойства: те же, что и теоремы вероятности(см. билет 4) |
|||||||||||||||||||||||||||||||||||||||||||||||
|
6 Теорема умножения Р(АВ)=Р(А) Р(В/А); Р(А1А2…Аn)=P(A1)P(A2/A1) P(A3/A1A2)…P(An/A1A2…An-1) – общая
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
4 Аксиоматическое определение вероятности. Следствия из определения. (А. Н. Колмогоров). Вероятностью случайного события А называется числовая функция, заданная на множестве Ã (где Ã- алгебра случайных событий удовлетворяющая следующим аксиомам: Аксиома неотрицательности: Р(А)0. Аксиома нормировки: Р()=1. Аксиома аддитивности: Р(А+В)=Р(А)+Р(В), если события А и В несовместны, т.е. А*В=ᴓ.
Дополнительная
аксиома для бесконечной последовательности
наблюдаемых событий: Р( Тройку (, Ã, р) называют вероятностным пространством. Основные теоремы
1)Р(
4)если
события А1,
А2,
…, Аn
–попарно несовместны, т.е. Аi
*A
j=ᴓ
(i то Р(А1+А2+…+Аn)=Р(А1)+Р(А2)+…+Р(Аn); 5)Теорема сложения для совместных событий: а) Р(А+В)= Р(А)+Р(В)-Р(АВ); b Формула для двух: P(A+B) = P(A) + P(B) –P(AB) (1)Вывод: A+B+C = (P(A)+P(B)-P(AB) )+ C (по ф-ле 1, A+B берем за А) = P(A) + P(B) + P(C) – P(AB) – P(AC) – P(BC) + P(ABC)
|
10 число элементов конечное или счётное : Ω= {ῳ1,ῳ2, ..., ῳn, …}Если каждому элементарному исходу ставится в соответствие число, т.е. имеем числовую функцию на множестве Ω,то говорят, что задана случайная величина. Эту функцию будем обозначать X. Значение функции X(ῳ )= x-число. Множество значений дискретной случайной величины X- будет конечным или счётным. Закон распределения дискретной случайной величины X- это ряд распределения x1x2… xn …
pi
=p{
X
=xi
}
(pi
– вероятность случайного события: «
Случайная величина X
принимает
Заметим,
что
Функцией распределения случайной величины Х называется числовая функция , которую обозначают F( х ), равную вероятности события { X x ),т.е. F ( х )=P { X x }. Функция распределения вычисляет вероятность попадания слева от точки х. Для дискретной случайной величины функция распределения задаётся следующей формулой:
F(
х ) = Свойства функции распределения Область определения: D( F )=(-∞; +∞ ). Множество значений : E(F )= [ 0, 1]. Монотонность : F( х )- неубывающая функции ,т.е.если х 1х2 ,то F ( х1) ≤F( х2) Непрерывность : В точка хi – функция имеет разрыв справа рода, при этом F (хi +0) –F ( xi- 0) =pi ( предел справа минус предел слева равен pi= P{ X =xi})
|
3 Определение алгебры случайных событий. Следствия из определений Множество Ã случайных событий, порожденных множеством Ω, называется алгеброй случайных событий, если выполнены условия:
1. Доказать: А ⋲ Алгебре, B ⋲ Алгебре => А*В ⋲ алгебре Доказательство: A*B влечет А, A*B влечет B => А*В ⋲ алгебре 2. Доказать: А ⋲ Алгебре, В ⋲ Алгебре => А-В ⋲ алгебре.
Доказательство:
А-В=А*
3. Доказать:
Доказательство:Ω
⋲
Алгебре,
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
18 Определение моды, медианы и квантили порядка «р». Число χp называется квантилью порядка р, если F(xp)=p или P{χ<xp}=p Медиана – квантиль порядка 0.5 Мода – точка максимума f(x) |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
7 Независимые события и их свойства
А
не зависит от В, если Р(А/В)=Р(А) при
Р(В) Р(А1 А2 …Аn)=P(A1) P(A2) …P(An).
Если
А и В независимые события, то они
обязательно совместные, т.к. Р(АВ) Теорема о сумме совместных, но независимых в совокупности событий.
Р(А1+А2+…+Аn)=1-p( Дано: P(A)*P(B)=P(A*B) Доказать:
P(A)*P(
P(
P( Доказательство:
|
8 Пусть H1, H2,…,Hn – наблюдаемые события для данного эксперимента, при чем они попарно несовместны (Hi*Hj=ᴓ) и образуют полную группу событий (H1+H2+…+Hn= Ω). Для
любого наблюдаемого в эксперименте
события A имеет место следующая
формула полной вероятности: События H1, H2,…, Hn принято называть гипотезами. Безусловные вероятности P(Hi), где i =1,.. ,n трактуются как доопытные (априорные) вероятности гипотез. Замечание: Формулу полной вероятности используют в условиях неопределенности, т.е. когда неизвестно, какая из гипотез Hi реализовалась.
Если событие
A реализовалось, то послеопытные
(апостериорные) вероятности гипотез
определяются по формулам
Байеса:
P(
|
9 1)Пусть проводится «n» независимых испытаний ( опытов).
2)В каждом опыте
возможны только два исхода: А (успех
) или
3)Р(А)=р; Р 4)Вероятность появления события А: Рn(к)= Сnk*pk*qn-k, (к=0, 1, 2, …, n). Вероятности Рn(к) называются биномиальнымии при этом справедливы формулы:
Pn(1) +…+Pn(n)=1- qn.
3.Вероятность
того, что А появится не менее «m»
раз: Pn(m)+
Pn(m+1)+…+Pn(n)=
4.Вероятность
того, что А появится не более «m»
раз: Рn(0)+
Pn(1)
+…+Pn(m)= n*p – q ≤k0≤n*p+p. – ф-ла наивероятнейшего
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
13 Числовые характеристики непрерывной случайной величины
D[X]=
|
14 Свойства математического ожидания 1. M[C] =С, ( С- константа)Место для формулы. 2. М[АX+ C] =АM[X] + C 3.M[АX +BY+C] =AM[x] +BM[Y] +C, (Х., Y-случайные величины; A, B- числа; С – константа) 4.Если X и Y независимые случайные величины, т.е. для любых х,y верно: P{(X<x)(Y<y)} = P{X<x}P{Y<y}. то M[XY] = M[X]*M[Y] 5. Если Y=A(X) (Y функция случайной величины X),то M[Y]=∑A(хi)*Pi (M[x2] = ∑ х2i*Pi ) Используя свойства математического ожидания, можно получить формулу для вычисления D[X] = M[(X- mx)2] = M[X2- 2*mx*X +(mx)2] = M[X2]-2*mx*M[X] + (mx)2 = M[X2]-(mx)2
|
15 Свойства дисперсии и среднеквадратичного отклонения. D[X] =M[X2] –m2[x] Заметим: ∑ хi2pi= M[X2] Свойства дисперсии и СКО
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
16 Основные дискретные распределения (способы задания и числовые характеристики): 1)биномиальное 2)распределение Пуассона 3)геометрическое распределение. Биномиальное распределение Х –число появлений события А в «n» независимых испытаниях Бернулли P{X=k}= Pn(к)=Cnkpk*qn-k, к=0,1,…,n
M[X]=
n*p,
D[X]=npq,
[X]= Распределение Пуассона Случайная величина Х распределена по закону Пуассона с параметром , если Pk=P{X=k}=()k/k!*e-, к=0,1,2,…,n,… Т.к. имеем счётное множество значений, то числовой ряд ∑pк=1 (числовой ряд сходится и сумма ряда равна 1)
M[X]==D[X]=;
[X]=
Распределение
Пуассона является предельным для
биномиального: Pn(k)k/k!*e-
n Геометрическое распределение Пусть в одном опыте событие А появляется с вероятностью р ,т. е. Р(А)=р, Р(Ā)= 1-р=q Опыты проводятся до первого появления события А. Х – число опытов. рк=Р{X=k}=qk-1p, к=1,.2,.3.,…,n,… Заметим, что выполнено условие: ∑рк =1 ( числовой ряд сходится и его сумма равна 1 )
М[X]=1/p, D[X]=q/p2 |
11 Числовые характеристики дискретной случайной величины 1)Математическое ожидание определяет средне статистическое значение случайной величины или центр распределения вычисляют по формуле: mx=M[ X ] = ∑ хi*pi ( В случае бесконечного числа значений случайной величины числовой ряд должен сходится ). 2)Дисперсия случайной величины (определяет меру рассеяния относительно центра распределения ) вычисляется по формуле: D [Х] =M[ ( X – mx)2] D[ X ]=∑ ( хi – mx )2*pi 3)
Среднее квадратичное отклонение х
=[
x]
= 4)Начальные моменты «к» го порядка к =М[ X k ]=∑хik *pi 1= M[X ]. 5) Центральные моменты «к» го порядка к =M[(Х –mx)k] ,1=0, 2= D[x]
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
12 Непрерывная случайная величина. Свойства функции плотности. Функция распределения непр. сл. в. и ее свойства Если множество значений случайной величины Х есть некоторый интервал или объединение интервалов числовой оси, то говорят о непрерывной случайной величине. 1)f(x) Основное
свойство функции плотности
Функция распределения непрерывной случайной величины F(x)=P{X<x}=
P{-∞<X<x}=
F`(x)=f(x) Заметим,
что p{ Основные свойства функции распределения F(x) непрерывной случайной величины. 1.Область
определения D(F)=(- 2.Множество
значений E(F)=[0;1]
или (0;1), при этом
3.Монотонность:
Неубывающая: т.е. если x1>x2,
F(x1) 4.Непрерывная функция 5.Для вычисления вероятности попадания в интервал справедливы следующие формулы: P{X< P{X P{
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
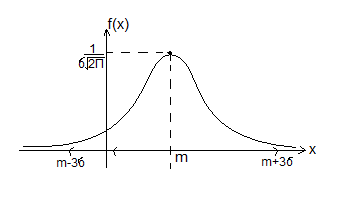
17 Основные непрерывные распределения (способы задания и числовые характеристики) 1)равномерное распределение на отрезке, 2)показательное распределение, 3)нормальное распределение.
Случайная величина Х называется равномерно распределённой на отрезке [a;b], если её функция плотности задаётся формулой
f(x)=
M[X]=
X
распределена по показательному закону
с параметром а, если функция плотности
задаётся формулой: f(x)=
F(x)= M[χ]=1/a; D[χ]=1/a2; σx=1/a 3) Нормальное распределение (закон Гаусса) с параметрами m, σ (обозначается: N (m, σ) M[χ]=m; D[χ]= σ2
Случайная
величина χ распределена нормально с
параметрами m,
σ, если функция плотности задается
формулой
f(x)=
Если
m=0,
σ=1,
то имеем стандартизированную случайную
величину. Функция плотности: (x)= [есть таблица значений этой функции] Функция распределения
F(x)=
Чтобы
найти значения функции распределения
используют таблицу значений функции
Лапласа
Ф(x)= Ф(-x)=- Ф(x) Ф(х)=1/2 F(x)=0,5+Ф((x-m)/σ) Основные формулы для вычисления вероятностей попадания в интервалы 1. Р{χ<α}=0,5+Ф((α-m)/σ) 2. P{χ>β}=0,5- Ф((β-m)/σ) 3. P{α<χ<β}=Ф((β-m)/σ)-Ф((α-m)/σ) 4. P{|χ-mx|<ε}=2Ф(ε/σ) 5. P{|χ-mx|<kσ}=2Ф(k) В частности: Правило “3σ”: P{|χ-mx|<3σ}=2Ф(3)=0,9973
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
19 Функция одномерной случайной величины. Законы распределения для дискретной и непрерывной случайной величины.
Пусть
Пусть
(каждому
возможному значению случайной величины
Все
значения случайной величины
при
этом
так
как
Если
строго убывает, то
Если
функция
Если
Если
(
Таким
образом, если
(1)
Если
(2)
Объединив (1) и (2) получаем:
если
Если
Если
При
решении задач на нахождение плотности
Дано
Найти
1.
Строим график
|
|||||||||||||||||||||||||||||||||||||||||||||||||

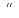
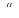 =
=
 +А = А
+А = А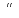
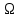 =
Ω * А = А
=
Ω * А = А =
А 2. А+Ā = Ω 3. А * Ā =
=
А 2. А+Ā = Ω 3. А * Ā =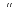 4.
4.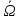 =
=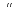 5.
5. = Ω
= Ω
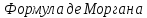
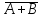 =
=
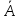 *
* ;
;
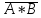 =
=
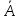 +
+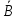
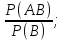 Р(В)
Р(В) ;
А
не зависит от В. если Р(А/В)=Р(А).
;
А
не зависит от В. если Р(А/В)=Р(А).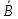 ,
,
 не зависит от В,
не зависит от В,
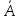 не зависит от
не зависит от
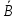 .
.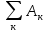 )=
)= , где события А1,…,Аn-
попарно несовместны, т.е. Аi
Aj=ᴓ
(i
, где события А1,…,Аn-
попарно несовместны, т.е. Аi
Aj=ᴓ
(i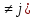
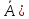 =1-Р(А);
2) Р(ᴓ)=0; 3)если А
В, то р(А)≤р(В)0≤
р(А)≤1;
=1-Р(А);
2) Р(ᴓ)=0; 3)если А
В, то р(А)≤р(В)0≤
р(А)≤1;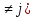 ;
;
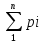 I
= 1
I
= 1 =
=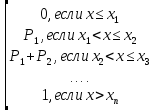
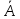 ⋲ Ã
[множество замкнуто относительно
основных операций]
⋲ Ã
[множество замкнуто относительно
основных операций]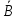 => см 1
=> см 1
 ⋲
Алгебре
⋲
Алгебре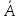 ⋲
Алгебре если А ⋲
Алгебре =>
⋲
Алгебре если А ⋲
Алгебре =>
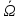 ⋲
Алгебре =>
⋲
Алгебре =>
 ⋲
Алгебре
⋲
Алгебре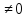
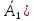 P(
P( )
… P(
)
… P(
 )
= P(A*
)
= P(A*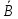 )
)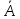 )*P(B)
= P(
)*P(B)
= P(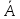 *B)
*B)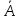 )*
P(
)*
P(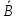 )
=P(
)
=P(
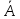 *
*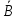 )
)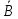 )
= - P(A) *P(B) + P(A) = P(A) – P(A)*P(B) = P(A*
)
= - P(A) *P(B) + P(A) = P(A) – P(A)*P(B) = P(A*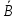 ),
чтд
),
чтд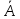 )*
P(
)*
P( )
= 1 – P(A)
– P(B)
+ P(AB)=
1- P(A+B),
след. по теореме о сумме совместных
независимых событий
P(
)
= 1 – P(A)
– P(B)
+ P(AB)=
1- P(A+B),
след. по теореме о сумме совместных
независимых событий
P(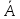 )*
P(
)*
P( )
=P(
)
=P(
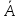 *
*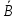 )
)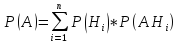
 )
=
)
=
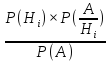 ,
i=
,
i=
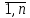 ;
;
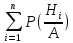 = 1
= 1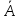 (
неудача).
(
неудача).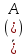 =q=1-р.
=q=1-р.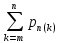 =1-
=1-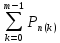
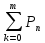 (k)
=1-
(k)
=1-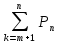 (k).
(k).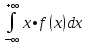 [математическое
ожидание D[X]=M[X2]-mx2
[дисперсия]
[математическое
ожидание D[X]=M[X2]-mx2
[дисперсия]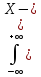 mx)2•f(x)dx
mx)2•f(x)dx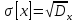 -среднее
квадратическое отклонение Начальные
моменты «кго»
порядка
-среднее
квадратическое отклонение Начальные
моменты «кго»
порядка
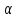 к=M[Xк]=
к=M[Xк]=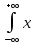 к•f(x)dx
к•f(x)dx «кго»
порядка
«кго»
порядка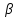 к=M[(X-mX)к]=
к=M[(X-mX)к]=
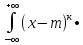 f(x)dx
f(x)dx
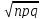
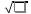
 ,где
=n*p
,где
=n*p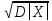
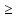 0
2)p
0
2)p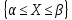 =
=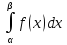
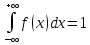

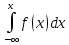
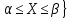 =
=
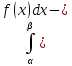 вероятность попадания в интервал
численно равна площади криволинейной
трапеции под кривой f(x).
вероятность попадания в интервал
численно равна площади криволинейной
трапеции под кривой f(x).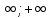 )
)
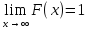
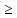 F(x2)
[нет точек extr]
F(x2)
[нет точек extr]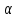 }
= F(
}
= F(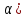
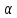 }
= 1 - F(
}
= 1 - F(
 }
= P{
}
= P{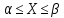 }
= P{
}
= P{ }
= P{
}
= P{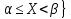 = F(
= F( F(
F(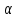 )
)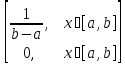 F(x)=
F(x)=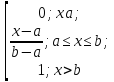 функция
распределения
функция
распределения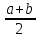 ;
D[X]=
;
D[X]=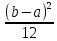 ;
X=
;
X=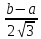
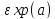
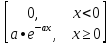
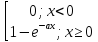
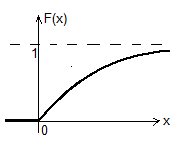
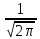 *
*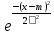

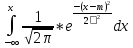

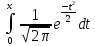
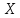 – дискретная случайная величина,
заданная рядом распределения:
– дискретная случайная величина,
заданная рядом распределения: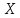
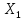

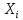

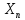


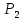
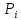
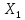

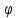 – неслучайная функция:
– неслучайная функция:
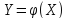
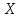 ставится в соответствии одно значение
случайной величины
ставится в соответствии одно значение
случайной величины
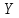 ).
).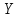 вычисляем по формуле:
вычисляем по формуле:
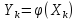 ,
,
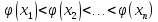
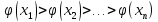
 имеет интервалы монотонности, то если
имеет интервалы монотонности, то если
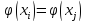 ,
то в таблице заносим одно значение, а
соответствующие вероятности
складываются.
,
то в таблице заносим одно значение, а
соответствующие вероятности
складываются.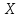 непрерывная случайная величина
непрерывная случайная величина
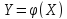 ,
причем
,
причем
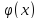 монотонно возрастающая непрерывно
дифференцируемая функция, то
монотонно возрастающая непрерывно
дифференцируемая функция, то
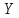 – тоже непрерывная случайная величина.
– тоже непрерывная случайная величина.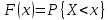 – распределения случайной величины,
то
– распределения случайной величины,
то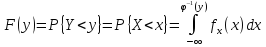
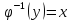 – функция обратная для функции
– функция обратная для функции
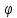 )
)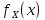 функция плотности с.в.
функция плотности с.в.
 ,
то
,
то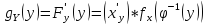
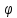 строго убывает, то
строго убывает, то
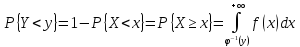
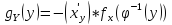
 строго монотонная функция, то для
нахождения функции плотности с.в.
строго монотонная функция, то для
нахождения функции плотности с.в.
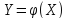 используем формулу:
используем формулу: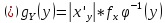 где
где
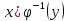
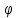 – функция не монотонна, то разбиваем
множество возможных значений
– функция не монотонна, то разбиваем
множество возможных значений
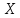 на интервалы монотонности
на интервалы монотонности
 ,
,
 ,
… ,
,
… ,
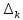 и на каждом интервале находим обратную
функцию
и на каждом интервале находим обратную
функцию
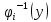 ,
то где плотность случайной величины
,
то где плотность случайной величины
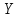 :
определяется в виде суммы:
:
определяется в виде суммы:
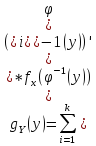 Полезная
информация
Полезная
информация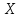 имеет функцию плотности
имеет функцию плотности
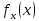 ,
а
,
а
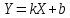 ,
то закон распределения с.в.
,
то закон распределения с.в.
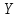 не меняется и при этом:
не меняется и при этом:
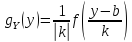
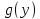 можно придерживаться следующей схемы.
можно придерживаться следующей схемы.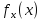

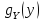
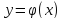 Пусть
Пусть
 строго монотонна Находим:
строго монотонна Находим:
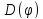 (область определения с учетом значения
с.в.
(область определения с учетом значения
с.в.
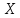 )
)
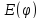 – множество значений 2. Находим
обратную функцию
– множество значений 2. Находим
обратную функцию
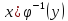 3.
Вычисляем
3.
Вычисляем
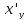 ,
,
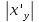 4.
4.
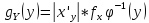 где
где