5,56	5,43	5,47	5,47	5,33	5,37	5,43	5,54	5,61
5,33	5,43	5,61	5,11	5,43	5,33	5,54	5,33	5,11
5,54	5,43	5,33	5,54	5,43	5,43	5,43	5,33	5,11
5,43	5,43	5,43	5,33	5,4	5,43	5,47	5,68	5,47
5,43	5,68	5,21	5,33	5,58	5,47	5,47	5,21	5,54
5,64	5,47	5,27	5,27	5,37	5,33	5,47	5,47	5,54
5,4	5,58	5,47	5,27	5,05	5,79	5,79	5,64	5,64
5,71	5,85	5,47	5,47	5,43	5,47	5,54	5,64	5,64
5,79	5,03	5,33	5,68	5,43	5,61	5,54	5,64	5,54
5,39	5,33	5,21	5,68	5,54	5,33	5,21	5,21	5,81
5,27	5,64	5,27	5,27	5,33	5,37	5,27	5,54	5,54
5,47

Таблица. .1

Пример. По результатам выборочного исследования 100 однотипных предприятий получены данные объема основных фондов

1. Построение интервального вариационного ряда распределения

Построение интервального вариационного ряда распределения включает следующие этапы.

1. Определение среди имеющихся наблюдений минимального и максимальногозначения признака. В данном примере это будут=5,03 и=5,85.

2. Определение размаха варьирования признака R=-=5,85-5,03=0,82

3.Определение длины интервала по формуле объем выборки. В данном примере

4. Определение граничных значений интервалов . Так какиявляются случайными величинами, рекомендуется отступить влево от нижнего предела варьирования ().

За нижнюю границу первого интервала предлагается принимать величину, равную . Если окажется, что, хотя по смыслу величина не отрицательная, то можно принять.

Верхняя граница первого интервала . Тогда, если–верхняя границаi-го интервала (причём ), то,и т.д. Построение интервалов продолжается до тех пор, пока начало следующего по порядку интервала не будет равным или больше.

В примере граничные значения составят:

, ,,и т.д.Границы последовательных интервалов записывают в графе 1 таблицы 1.2.

5. Группировка результатов наблюдений.

Просматриваем статистические данные в том порядке, в каком они записаны в таблице 1.1, и значения признака разносим по соответствующим интервалам, обозначая их так (по одному штриху для каждого наблюдения). Так как граничные значения признака могут совпадать с границами интервалов, то условимся включать варианты, большие, чем нижняя граница интервала (), и меньшие или равные верхней границе (). Общее количество штрихов, отмеченных в интервале (табл. 1.2, графа 2) дает его частоту (табл. 1.2, графа 3). В результате получим статистический ряд распределения частот (табл. 1.2, графа 1 и 3).

Примечание. Число интервалов обычно берут равным от 7 до 11 в зависимости от числа наблюдений и точности измерений с таким расчетом, чтобы интервалы были достаточно наполнены частотами. Если получают интервалы с нулевыми частотами, то нужно увеличить ширину интервала (особенно в середине интервального ряда).

Интервалы	Подсчет частот	Частота	Накопленная частота
4,97-5,08 5,08-5,19 5,19-5,30 5,30-5,41 5,41-5,52 5,52-5,63 5,63-5,74 5,74-5,85		2 3 12 19 29 18 13 4	2 5 17 36 65 83 96 100
		100

Таблица 1.2. Интервальный ряд распределения объемов основных фондов 100 предприятий

2. Вычисление выборочных характеристик распределения (непосредственно)

Для вычисления средней арифметической, дисперсии, коэффициентов ассиметрии и эксцесса рекомендуется следующий порядок вычислений.

Заменяем интервальный ряд дискретным, для чего все значения признака в пределах интервала приравниваем к его серединному значению, и считаем, что частота относится к середине интервала. Значения середин интервалов равны .

Для удобства вычислений целесообразно составить вспомогательную таблицу 1.3. Заменяя середины интервалов заносят в графу 1, соответствующие частоты в графу и т.д.

Интервалы
1	2	3	4	5	6	7
4,97-5,08 5,08-5,19 5,19-5,30 5,30-5,41 5,41-5,52 5,52-5,63 5,63-5,74 5,74-5,85	5,03 5,14 5,25 5,36 5,47 5,58 5,69 5,80	2 3 12 19 29 18 13 4	2 5 17 36 65 83 96 100	10,06 15,42 63,00 101,84 158,63 100,44 73,97 23,20	50,60 79,26 330,75 545,86 867,71 560,46 420,89 134,56	-0,4356 -0,3256 -0,2156 -0,1056 0,0044 0,1144 0,2244 0,3344
		100		546,56	2990,09

Таблица 1.3 Вспомогательная таблица для вычисления выборочных характеристик

8	9	10	11
-0,8712 -0,9768 -2,5872 -2,0064 0,1276 2,0592 2,9172 1,3376	0,37949 0,31805 0,55780 0,21188 0,00056 0,23557 0,65462 0,44729	-0,1653 -0,10356 -0,12026 -0,02237 0,00000 0,02695 0,14690 0,14957	0,07201 0,03372 0,025928 0,00236 0,00000 0,00308 0,03296 0,05002
0	2,80526	0,08808	0,22008

В таблице .

Пользуясь таблицей 1.3, вычислим среднюю арифметическую: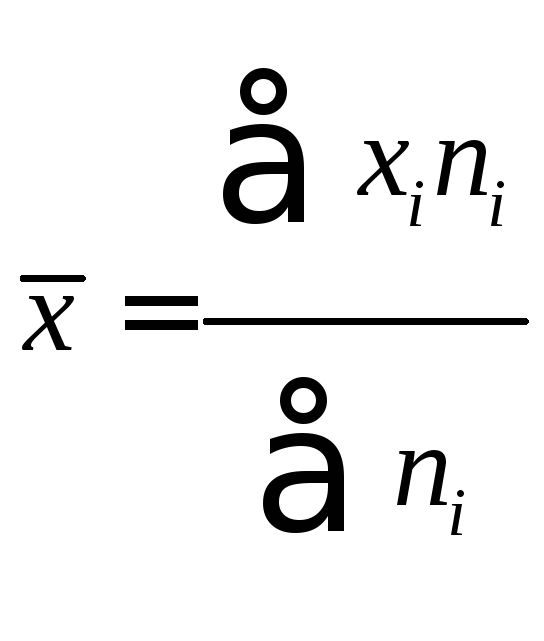. В нашем примеремлн. руб. и характеризует среднее положение наблюдаемых значений. Выборочный центральный момент к-го порядка равен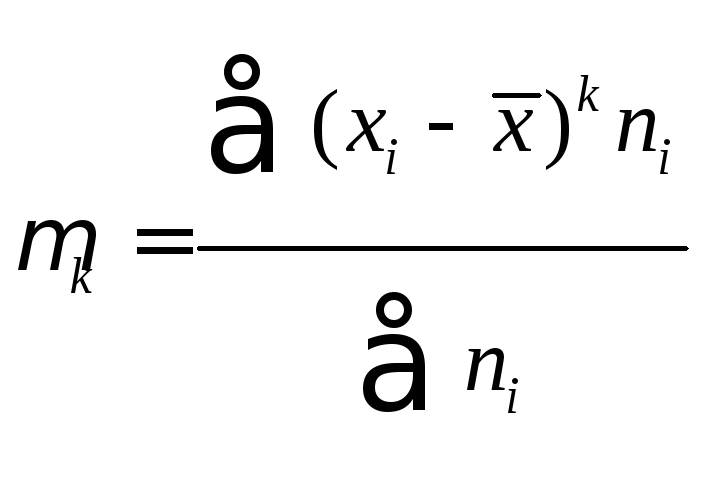. Для проверки правильности вычисленияи ввода в микрокалькулятор значений,рассчитывают:

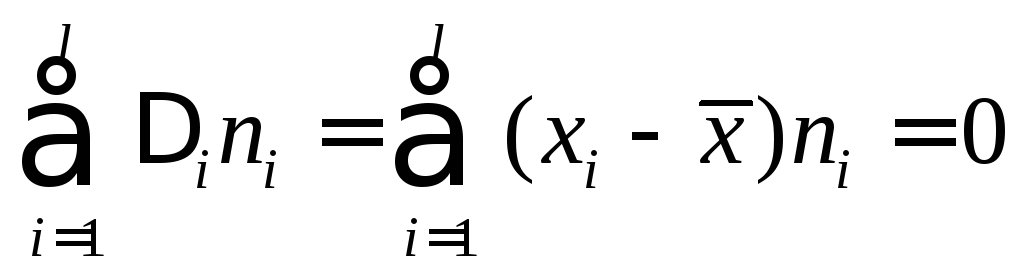
В нашем примере тождество выполняется. В итоговой строке столбца 4 табл. 1.3. имеем 0.

В данном примере .

Выборочная дисперсия равна центральному моменту второго порядка:

==.

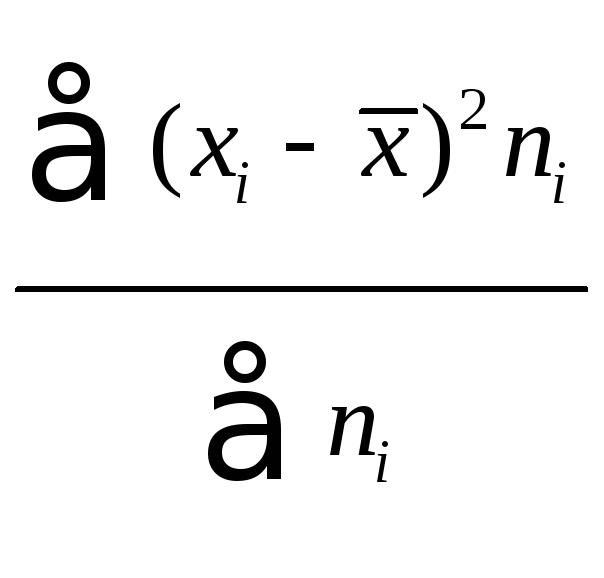В нашем примере =0,028, а выборочное среднее квадратичное отклонениемлн.руб.

Дисперсию можно подсчитать и по-другому

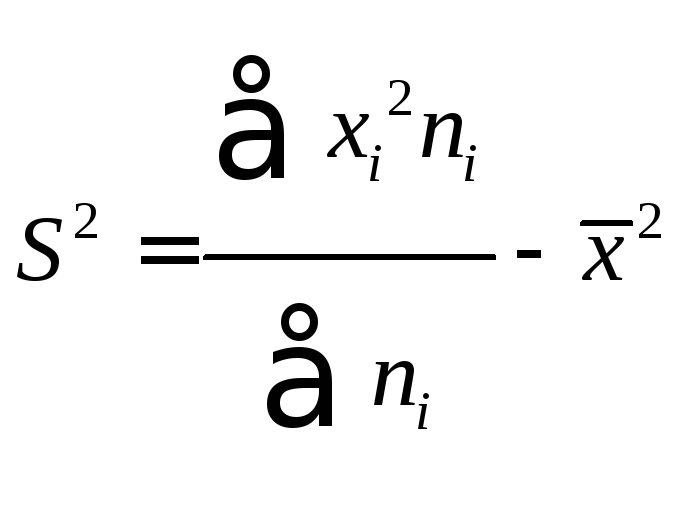
В нашем примере

Выборочные коэффициенты асимметрии

.