15. Момент инерции однородных, диска, стержня, шара. Теорема Штейнера

Моменты инерции некоторых тел массой m относительно оси z, проходящей через центр масс:

а) стержня длиной l относительно оси, перпендикулярной стержню и проходящей через его середину ,

б) обруча (тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча и проходящей через его центр , где R — радиус обруча (цилиндра);

в) диска радиусом R относительно оси, перпендикулярной плоскости диска ,

г) шара радиусом R относительно оси, проходящей через его центр .

Теорема Штейнера: Момент инерции тела массой m относительно произвольной оси z, не проходящей через центр масс, равен моменту инерции J_c относительно оси, проходящей через центр масс и параллельной оси z, плюс произведение массы тела на квадрат расстояния между осями

.

16. Гармонические колебания. Уравнение свободных колебаний и его решение. Скорость и ускорение колеблющейся точки. Энергия гармонического колебания.

Колебания, которые проходят по закону синуса или косинуса, называются гармоническими. Уравнение гармонических колебаний материальной точки

,

где х — смещение точки от положения равновесия; А — амплитуда колебаний; ω — круговая или циклическая частота;  — начальная фаза.

Скорость и ускорение материальной точки, совершающей гармонические колебания:

и .

Энергия гармонического колебания:

17. Математический, пружинный и физический маятники. Приведенная длина физического маятника. Центр качаний.

Математический маятник представляет собой материальную точку, подвешенную на невесомой нерастяжимой нити и способную совершать колебания в поле сил тяжести Земли.

Период математического маятника , где l –длина математического маятника.

Пружинный маятник представляет собой тело массы m, связанное с упругой пружиной жесткостью k.

Период пружинного маятника , где k — коэффициент жесткости пружины.

Физический маятник представляет собой абсолютно твердое, способное совершать колебания в поле сил тяжести Земли вокруг горизонтальной оси, не проходящей через его центр тяжести.

Период физического маятника

,

где J – момент инерции физического маятника относительно горизонтальной оси, не проходящей через центр масс, d – расстояние от оси до центра масс.

Приведенная длина физического маятника – длина математического маятника с таким же периодом колебаний.

Центр качаний – точка, находящаяся на расстоянии приведенной длины от оси и расположенная на прямой, проходящей через ось и центр масс. При переносе оси в цент качаний период физического маятника не изменяется

18. Вынужденные колебания. Резонанс. Резонансные кривые.

Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью вынуждающей силы, изменяющейся по гармоническому закону:

F = F_m cos t,

где  - циклическая частота вынуждающей силы.

Дифференциальное уравнение для вынужденных колебаний имеет вид

. (1)

Здесь x – смещение колеблющейся точки относительно положения равновесия, - коэффициент затухания, ₀ - циклическая частота собственных колебаний.

В установившемся режиме вынужденные колебания происходят с частотой  и являются гармоническими. Решение уравнения (1) для установившегося режима имеет вид

. (2)

Причем амплитуда A и фаза  зависят от , ₀, , x₀

, . (3)

Амплитудные резонансные кривые построенные на основе (3), приведены на рис.1.

Явление резкого возрастания амплитуды вынужденных колебаний на некоторой частоте, называемой резонансной (которая для малого затухания совпадает с частотой собственных колебаний ₀) называется резонансом .

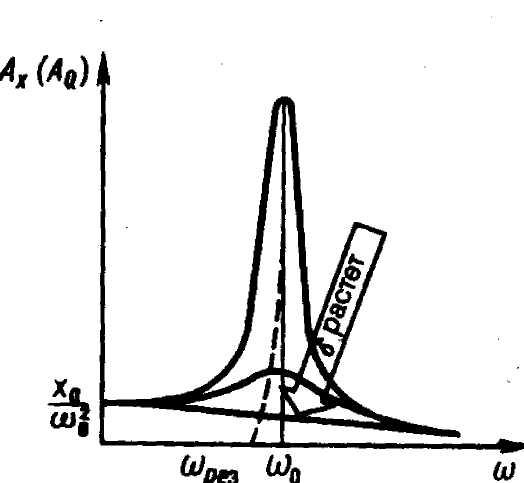
Рис.1.

Чем больше коэффициент затухания, тем ниже амплитуда при резонансе.

Амплитуда при резонансе A_res связана со статическим отклонением (при  стремящейся к нулю) через добротность Q:

A_res=QA_st, где.

Чем выше добротность контура, тем выше амплитуда при резонансе.

Фазовая резонансные кривые построенные на основе (3), приведены на рис.2.

Рис.2.

Видно, что только в случае когда затухания нет (=0), вынуждающая сила и колебания совпадают по фазе.

Явления резонанса могут быть как вредными, так и полезными. Например, при конструировании машин и различного рода сооружений необходимо, чтобы собственная частота колебаний их не совпадала с частотой возможных внешних воздействий, в противном случае возникнут вибрации, которые могут вызвать серьезные разрушения. С другой стороны, наличие резонанса позволяет обнаружить даже очень слабые колебания, если их частота совпадает с частотой собственных, колебаний прибора. Так, радиотехника, прикладная акустика, оборудование, воспринимающее электрические колебания, основаны на явлении резонанс.