3. Предел функции

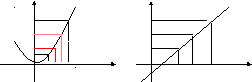
Рассмотрим графики функций. Сравним поведение каждой функции вблизи точки =2.

а) б)

в)г)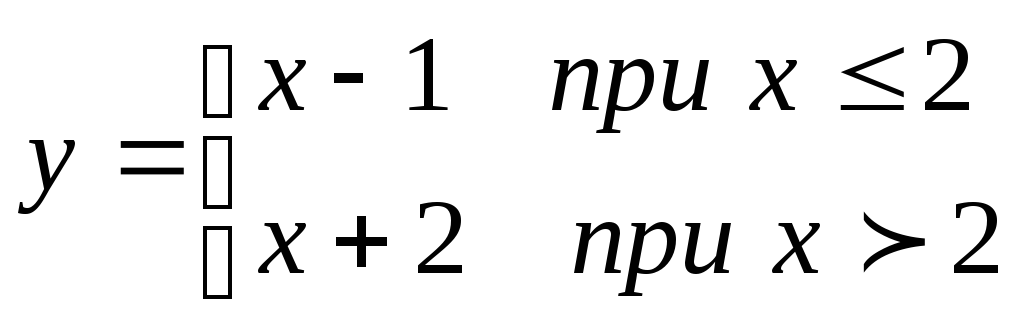

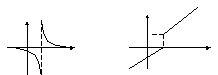
9

Определение:ЧислоАназываетсяпределом функцииy=f(x)

в точке, если для любого положительногоεнайдется такое положительное числоδ, зависящее отε, что для всехх≠х,удовлетворяющих неравенству |х-|<δ, выполняется неравенство |f(x)-A|<ε:.

Это определение коротко можно записать так:

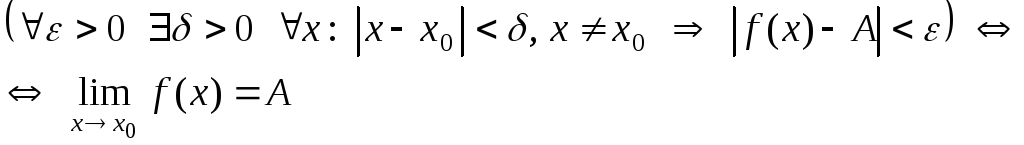
Предел функции при х

Существуют функции, у которых при . Например:

Пусть функция y=f(x)определена на промежутке (-∞;∞). Число А называетсяпределом функции при х→∞, если для любого положительного числа ε существует такое число М=М(ε)>0, что при всех х, удовлетворяющих неравенству |х|>М выполняется неравенство |f(x)-A|<ε. Коротко это определение можно записать так:

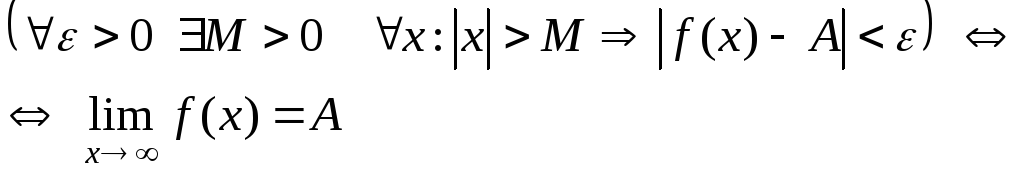
Если х→+∞, то пишут , если х→ - ∞, то -.

10

4. Бесконечно малые и бесконечно большие функции

Функция y=f(x)называетсябесконечно малой(илибесконечно малой величиной) при, если. Например,б.м. при х→0, т.к.f(x) →0, т.е..

Аналогично определяется б.м.ф. при х→±∞,+ и-.

Свойства бесконечно малых функций

1. Алгебраическая сумма конечного числа б.м.ф. есть б.м.ф.

2. Произведение б.м.ф. на ограниченную функцию есть б.м.ф. (в том числе на постоянную или на другую б.м.ф.).

3. Частное от деления б.м.ф., предел которой отличен от 0, есть б.м.ф.

Функция y=f(x)называетсябесконечно большой(илибесконечно большой величиной) при, если. Например,б.б.ф. при, т.к.f(x)→ ∞ илиy=tgxприхб.б.ф.

Аналогично определяется б.б.ф. при х→±∞, + и-.

Если f(x) → ∞ прии принимает лишь положительные значения, то пишут, если лишь отрицательные, то.

Свойства бесконечно больших функций:

1. Произведение б.б.ф. на функцию, предел которой отличен от 0, есть б.б.ф.

2. Сумма б.б.ф. и ограниченной функции есть б.б.ф.

3. Частное от деления б.б.ф. на функцию, имеющую предел, есть б.б.ф.

11

Связь между бесконечно малыми и бесконечно большими функциями

Теорема:Если функция α (х) – бесконечно малая при, то

функция является бесконечно большой при

, и наоборот.

5. Основные теоремы о пределах

1. Функция не может иметь более одного предела.

2. Предел суммы (разности) двух функций равен сумме (разности) их пределов:

3. Предел произведения двух функций равен произведению их пределов:

4. Постоянный множитель можно выносить за знак предела:

.

5. Предел степени с натуральным показателем равен той же степени предела:

6. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен 0:

.

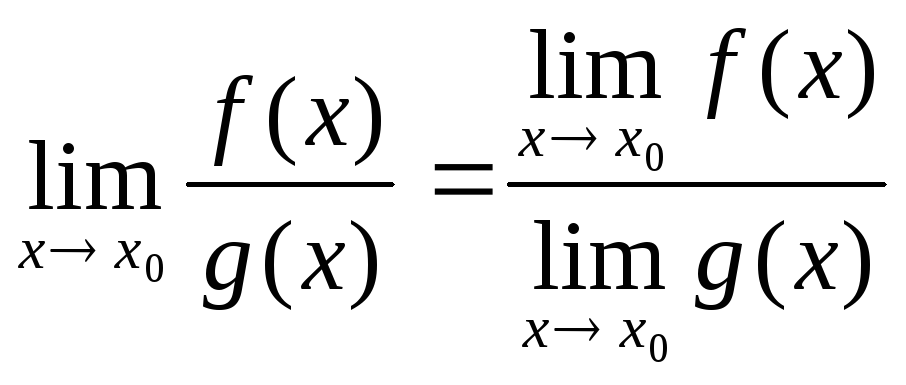7. Если - предел сложной функции.

8. Если в некоторой окрестности точки (или при достаточно большихх)f(x)<g(x), то.

12