Пределы числовой последовательности и функции

1. Числовые последовательности

Числовые последовательности представляют собой бесконечное множество чисел. Примером являются арифметическая и геометрическая прогрессии.

Числовой последовательностьюназывается множество чисел, все элементы которого пронумерованы всеми натуральными числами. Обозначаются:. Числаназываютсяэлементами иличленами последовательности, символ-общимилиn-м членом последовательности,n- егономером. При этом не предполагается, что элементы с различными номерами сами должны быть различны.

Последовательность задана, если для любого номера nопределено правило нахождения элемента последовательности с этим номером.

Чаще всего последовательность задают формулой его общего члена. Формула позволяет вычислить любой член последовательности по его номеру n. Например,

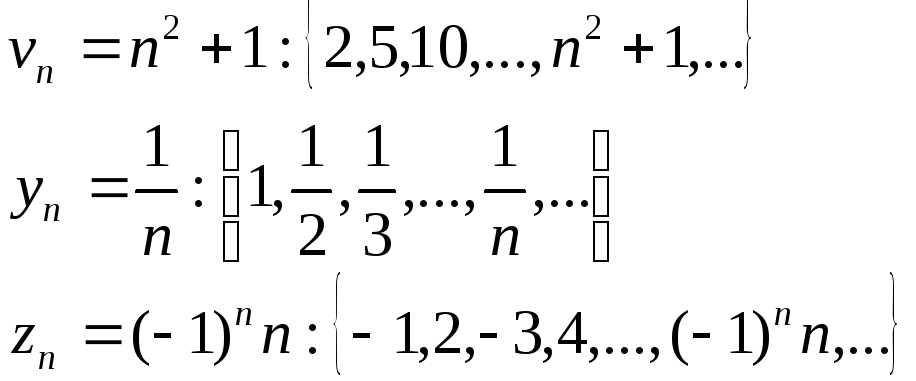
Последовательность называется ограниченной, если существует такое число М>0, что для любогоnNвыполняется неравенство:. В противном случае последовательность называетсянеограниченной. Т.о.- неограниченные,- ограниченная.

Последовательность называетсявозрастающей (неубывающей), если для любогоnвыполняется неравенство. Аналогично определяетсяубывающая (невозрастающая)последовательность.

1

Все эти последовательности называются монотонными. Последовательность- не монотонная,- монотонные.

Рассмотрим пример числовой последовательности . Изобразим ее члены точками числовой оси

| | | |  | | | | |

Можно заметить, что члены последовательности с ростомnкак угодно близко приближаются к 1. При этом расстояние, т.е.становится все меньше и меньше.

Определение:Числоаназываетсяпределом последовательности, если для любого положительного числа ε существует такой номерN, что при всехn>Nвыполняется неравенство:. (1)

В этом случае пишут и говорят, что последовательностьимеет предел, равный числуа. Говорят также, что последовательностьсходится к аили называетсясходящейся. Последовательность, не имеющая предела, называетсярасходящейся.

Коротко определение предела можно записать так:

(Смысл кванторов: - существует, найдется;- для любого, любой;- «двоеточие» - такой, что).

2

Приведем геометрическую интерпретациюопределения предела последовательности:

( | | | | |||||||| | | | | | )

Неравенство (1) равносильно неравенству или, которые показывают, что элементнаходится вε–окрестности точкиа. Поскольку последовательность представляет собой бесконечное множество чисел, то, если она сходится, в любой ε–окрестности точкиа на числовой прямой находится бесконечное число точек – элементов этой последовательности, тогда как внеε–окрестности остается конечное число элементов.

Итак, число а есть предел числовой последовательности , если для любого ε>0найдется номер N, начиная с которого (при n>N) все члены последователь ности попадут в ε-окрестность точки а, какой бы узкой она не была.

Неограниченная последовательностьне имеетконечногопредела. Однако она может иметьбесконечныйпредел, что записывается в следующем виде:.

Если при этом, начиная с некоторого номера, все члены последовательности положительны (отрицательны), то пишут ().

Последовательность, имеющая своим пределом 0 (а=0), называетсябесконечно малой последовательностью. Если- бесконечно малая последовательность, то- бесконечно большая последовательность, имеющая бесконечный предел, и наоборот.

3

Свойства сходящихся последовательностей:

1. Если все элементы последовательности равны одному и тому же числу, то

2. Сходящаяся последовательность имеет только один предел.

3. Сходящаяся последовательность ограничена.

4. Сумма (разность) сходящихся последовательностей иесть сходящаяся последовательность, предел которой равен сумме (разности) пределов последовательностейи:+.

5. Произведение сходящихся последовательностей иесть сходящаяся последовательность, предел которой равен произведению пределов последовательностейи:.

6. Частное двух сходящихся последовательностей ипри условии, что предел последовательностиотличен от 0, есть сходящаяся последовательность, предел которой равен частному пределов последовательностейи.

7. Если элементы сходящейся последовательности удовлетворяют неравенствуначиная с некоторого номера, то и предела этой последовательности удовлетворяет неравенству.

8. Произведение бесконечно малой последовательности и ограниченной последовательности или числа есть бесконечно малая последовательность.

9. Произведение конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

4