Сложение комплексных чисел

Суммой двух комплексных чисел z1 = x1 + iy1 и z2 = x2 + iy2 называется число z = x + iy такое, что справедливы равенства

x = x1 + x2, y = y1 + y2, то есть z = z1 + z2 = ( x1 + x2) + i( y1 + y2) = x + iy.

Обозначение суммы: z = z1 + z2

При сложении комплексных чисел складываются действительные и мнимые части соответственно.

Вычитание комплексных чисел

Разностью чисел z1 и z2 называется число z такое, что z1 = z + z2.

Обозначение: z = z1 − z2

Формулы для вычитания

Используя правило сложения, получаем для нахождения разности z = z1 − z2, z = x + iy равенства x = x1 − x2, y = y1 − y2.

При нахождении разности z1 − z2 из действительной и мнимой частей уменьшаемого z1 вычитаются соответственно действительная и мнимая части вычитаемого:

z = ( x1 − x2) + ( y1 − y2) i .

Умножение комплексных чисел

Произведением чисел z1 = x1 + iy1 и z2 = x2 + iy2 называется число z = x + iy такое, что выполняются равенства x = x1 x2 − y1 y2, y = x1 y2 + x2 y1.

Обозначение для умножения комплексных чисел. z = z1 · z2

Формальное определение умножения комплексных чисел Нетрудно убедиться, что эти равенства имеют место, если произвести формальное перемножение выражений ( x1 + iy1)( x2 + iy2), как двучленов: ( x1 + iy1)( x2 + iy2) = x1 x2 + i x1 y2 + i y1 x2 + i2 y1 y2 = = ( x1 x2 − y1 y2) + i( x1 y2 + y1 x2)

Правило умножения мнимой единицы.

Комплексные числа перемножаются, как двучлены, при этом учитывается, что i² = −1.

Деление комплексных чисел

Частным от деления числа z1 на z2 ( z2 6= 0) называется число z, такое, что справедливо равенство z · z2 = z1.

Обозначение для деления: z =z1/z2

Возведение комплексного числа в степень

Извлечение корня из комплексного числа

Свойства операции комплексного сопряжения

2) Асимптоты. Общая схема построения графика функции.

Асимптоты

Геометрический смысл асимптоты

Общий метод отыскания асимптот

Общая схема построения графика функции

Этап 1 1. Определить область существования функции, область непрерывности и точки разрыва.

Этап 2 2. Найти асимптоты.

Этап 3

3. Приблизительно, вчерне, нарисовать график функции.

Этап 4 4. Вычислить первую, а если нужно, и вторую производную (без производных более высокого порядка часто удается обойтись)

Этап 5 5. Найти точки, в которых первая и вторая производные либо не существуют, либо равны нулю

Этап 6 6. Составить таблицу изменения знака первой и второй производных. Определить промежутки возрастания, убывания, выпуклости вверх или вниз функции, найти точки экстремума (в том числе концевые) и точки перегиба.

Этап 7 7. Окончательно вычертить график

3)Решить матричное уравнение

=

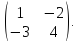
Билет №2

1) Комплексные числа в тригонометрической и показательной формах.

Тригонометрическая форма комплексного числа

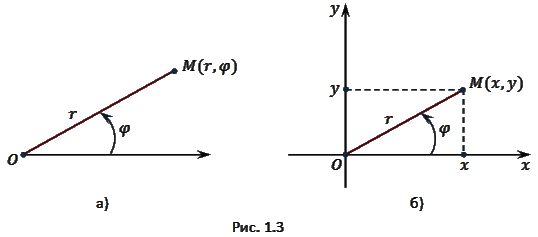
Переход из алгебраической в тригонометрическую форму

Показательная форма комплексного числа

Векторная интерпретация комплексных чисел

Модуль комплексного числа

Модуль и расстояние

Аргумент комплексного числа

Главное значение аргумента комплексного числа

Равенство комплексных чисел в тригонометрической форме

Умножение комплексных чисел в тригонометрической форме

Деление комплексных чисел в тригонометрической форме

Возведение в степень комплексного числа в тригонометрической форме

Извлечение корня из комплексного числа в тригонометрической форме

Правило извлечения корня из комплексного числа

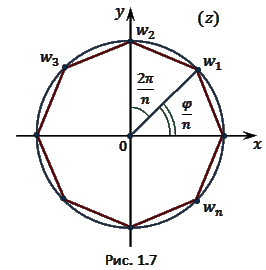
2)Исследование функций. Выпуклость функции и точки перегиба.

Выпуклость функции

Строгая выпуклость функции

Доказательство теоремы 5

Выпуклость и касательные

Точки перегиба

Замечание.

Первое достаточное условие для точки перегиба

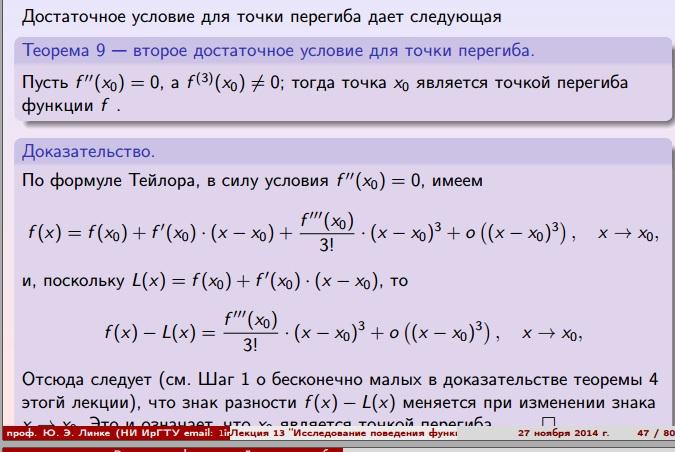
Доказательство

Второе достаточное условие для точки перегиба

Билет №3

1)Действительные или вещественные числа, различные формы аксиомы непрерывности.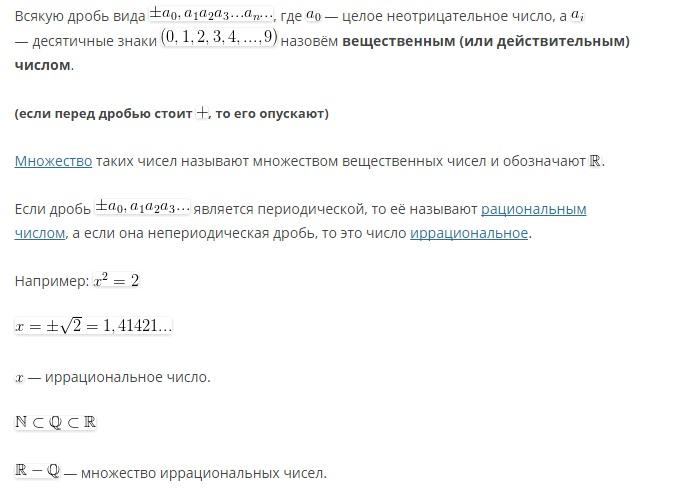

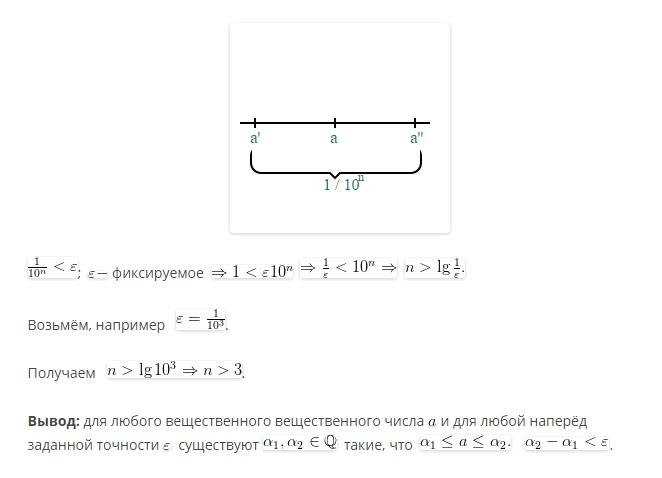
2)Исследование функций. Определение наибольших и наименьших значений.

Наблюдение о приращении функции для точек строгого экстремума

Необходимые условия экстремума

3)Решить матричное уравнение

Х=.

Билет №4

1)Числовые последовательности. Предел последовательности и его первая группа свойств.

2)Исследование функций. Признаки монотонности функций.

3)При каких значениях А и С прямая Ах+3y+C=0 параллельна прямой

3x-y+8=0.

Билет №5

1)Числовые последовательности. Предел последовательности и его вторая группа свойств

2) Единственность многочлена Тейлора.

3)Найти единичный вектор перпендикулярный каждому из векторов (3,-1,2) и (-1,3,-1).

Билет №6

1)Числовые последовательности. Предел последовательности. Бесконечно малые и большие последовательности и их свойства.

2)Формула Тейлора и Маклорена.

Его можно представить в виде суммы степеней , взятых с некоторыми коэффициентами. Продифференцируем егораз по переменной, а затем найдем значения многочлена и его производных в точке:

Таким образом, получаем, что

Полученное выражение называется формулой Маклорена для многочлена степени.

Рассуждая аналогично, можно разложить многочлен по степеням разности, где- любое число. В этом случае будем иметь:

Это выражение называется формулой Тейлора для многочлена в окрестности

точки .

3)Найти уравнение окружности, касающейся осей координат и проходящей через точку (4,-2).

Билет №7

1)Число 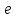как предел последовательности

Теорема. Последовательность с общим членом  имеет конечный предел при.  Замечание. Для обозначения этого предела используется символ e:

Число  e  является иррациональным, приближенное значение которого равно

e = 2.71828182845904523536028747135266249775724709…

Доказательство. Покажем сначала, что  представляет собой монотонно возрастающую последовательность. Согласно биному Ньютона,

 

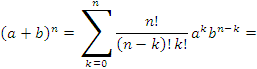
Полагая  , получим

 

Аналогично,

 

Сравним выражения для  и.  Во-первых, оба эти выражения содержат только положительные слагаемые.  Во-вторых, начиная со второго слагаемого, каждый член в выражении для  превышает соответствующий член выражения для, поскольку

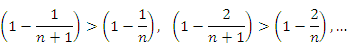
В-третьих, выражение для  состоит из большего числа слагаемых. Следовательно,  Далее докажем, что последовательность  является ограниченной. Действительно, первый член любой монотонно возрастающей последовательности является ее наибольшей нижней границей и, таким образом,для всех натуральных значенийn.  Перейдем к доказательству существования верхней границы. Очевидно, что

 

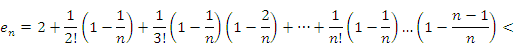
Кроме того,  для всехk > 3. Тогда

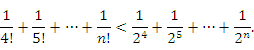
Правая часть этого неравенства представляет собой сумму членов убывающей геометрической прогрессии. В качестве верхней границы этой суммы выступает любое число  . Таким образом, последовательность с общим членом

представляет собой ограниченную монотонно возрастающую последовательность и, следовательно, имеет конечный предел – согласно теореме о монотонных последовательностях.