3 Подобрать по Mmax размеры двутаврового сечения
Для начала необходимо определить максимальное значение изгибающего момента Mmax – по модулю. Из эпюры Mx видно, что это значение равно 130 кНм.
Рассчитываем требуемый момент сопротивления сечения из условия прочности по нормальным напряжениям:
=
=
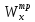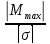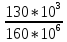= 0.8125*10-3
м3
= 812.5
см3
Теперь переходим к определению размеров двутаврового сечения:
По
таблице сортамента выбираем наиболее
подходящий двутавр – двутавр №
36:
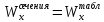= 743 см3
– ближайший
Площадь
сечения двутавровой балки: A
=
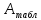= 61.9 см2
Поскольку момент сопротивления сечения несколько меньше требуемого, необходимо определить перегрузку по напряжениям:
=
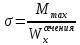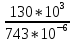= 174.97 МПа > [σ]
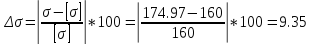
Так
как величина перегрузки
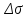– превышает 5%,
то при заданных нагрузках такая
конструкция не
является надежной.
В
таком случае из таблицы сортамента
выбираем следующий номер двутаврового
сечения – профиль
двутаврового сечения
№
40:
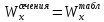= 947 см3
Площадь
сечения двутавровой балки: A
=
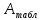= 71.4 см2
Поскольку момент сопротивления сечения несколько меньше требуемого, необходимо определить перегрузку по напряжениям:
=
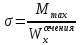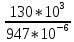=137.28
МПа < [σ]
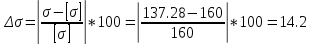
Так
как
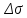– превышает 5%,
то при заданных нагрузках такая
конструкция является излишне
надежной.
4 Произвести полную проверку прочности (по нормальным, касательным и эквивалентным напряжениям) для двутаврового сечения
Для начала выпишем все необходимые данные для профиля двутаврового сечения из таблицы: Ix = 18390 см4, Wx = 947 см3, Sx = 540 см3, h = 40 см, b = 15.5 см, t = 1.3 см, d = 0.8 см.
Далее необходимо выбрать опасные сечения данной балки:
Сечение
I-I
– в этом сечении одновременно наблюдаются
максимальный изгибающий момент
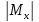= Mmax
= 130 кНм
и максимальная поперечная сила
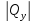= Qmax
= 130 кН.
Сечение
II-II
– в этом сечении наблюдается неблагоприятное
сочетание изгибающего момента
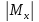= 20 кНм
и поперечной силы
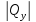= 90 кН.
Теперь подробнее рассмотрим каждое из этих опасных сечений:
В сечении I-I под рассмотрение попадают опасные точки 1 и 2 (см. приложение Б). В точках 1(1) будут наблюдаться наибольшие нормальные напряжения, а в точке 2 – наибольшие касательные напряжения.
Запишем условие прочности для опасной точки 1:
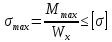
[σ] = 160 МПа – по условию
Следовательно,
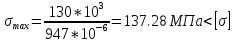
Следовательно, прочность по нормальным напряжениям для данной балки при заданных нагрузках обеспечена.
Теперь запишем условие прочности для опасной точки 2 – формулу Журавского:
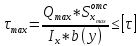
[τ] = 80 МПа – по условию
=
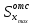Sxполусеч
= Sxтабл
= 540 см3
b(y) = d = 0.8 см
Следовательно,
Следовательно, прочность по касательным напряжениям для данной балки при заданных нагрузках обеспечена.
По соответствующим значениям найденных напряжений строим соответственно эпюры σ и τ (см. приложение Б).
В сечении II-II под рассмотрение попадает опасная точка 3(3) (см. приложение Б).
Следовательно, для опасной точки 3:
=
=
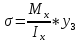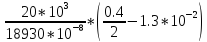=19.757
МПа
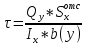
Sxотс
= Sxполки
= Aполки
* yc
=
=
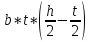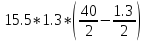= 389.9 см3
b(y) = d = 0.8 см
Следовательно,
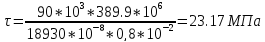
По соответствующим значениям найденных напряжений строим соответственно эпюры σ и τ (см. приложение Б).
Далее находим главные напряжения, которые равны соответственно:
=
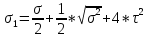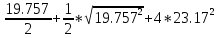=35.066
МПа
=
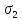0
=
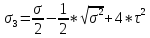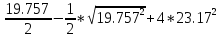=9.88
МПа
Наконец, найдем эквивалентное напряжение по III теории прочности:
=
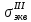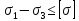
Следовательно,
=
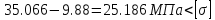
Отсюда видно, что и по эквивалентным напряжениям прочность данной балки обеспечена при заданных нагрузках.