Лекция №5
Взаимное расположение двух и трех плоскостей. Расстояние от точки до плоскости. Расстояние между двумя параллельными плоскостями. Угол между плоскостями.
Лемма 5.1.
(Условие
параллельности вектора и плоскости).
Пусть в
аффинной системе координат задана
плоскость
общим уравнением
и вектор
.
Вектор
параллелен плоскости
тогда
и только тогда, когда
выполняется условие:
.
Доказательство.
Пусть
.
Докажем, что выполняется условие
.
1.
Рассмотрим
.
Отложим
от неё вектор
.
2. Пусть
,
тогда вектор
.
Запишем условие равенства векторов
и
:
3. Так как
,
то
ее координаты удовлетворяют уравнению
плоскости, т.е.
,
где
(точка
принадлежит плоскости ).
(<=) повторить все рассуждения в обратном направлении.
Ч.т.д.
Лемма 5.2.
Пусть в
прямоугольной системе координат
плоскость
задана общим уравнением:
.
Тогда
вектор
перпендикулярен
плоскости
.
Доказательство.
Пусть
вектор
параллелен плоскости .
Применяя
условие параллельности вектора и
плоскости, получим:
вектор
перпендикулярен
плоскости
.
Ч.т.д.
Взаимное расположение двух плоскостей.
В аффинной системе
координат поверхность, заданная
уравнением первой степени, является
плоскостью. Выясним, при каких условиях
два уравнения
и
:
I. Определяют одну и ту же плоскость;
II. Определяют две параллельные плоскости;
III. Определяют две пересекающиеся плоскости.
I.
Условия, при которых уравнения
и
определяют
одну и ту же плоскость.
Теорема 5.3.
Для
того чтобы два
уравнения
и
в аффинной системе координат определяли
одну и ту же плоскость, необходимо и
достаточно, чтобы все коэффициенты в
уравнениях были пропорциональны.
Необходимость:
Дано: уравнения
плоскостей
:
(1)
(2)
Докажем:
.
Доказательство:
1.
Данные уравнения определяют одну и ту
же плоскость
.
Значит, векторы нормалей
и 
будут коллинеарны, т.е.
или
.
2.
Подставим выражения в уравнение (1) и
выразим
:
3.
Найдем отношение
:
.
4.
Значит,
Достаточность:
Дано:
уравнения:
:
(1)
(2)
.
Докажем,
что уравнения (1) и (2) задают одну и ту же
плоскость
.
Доказательство:
1.
Выразим из условия теоремы
коэффициенты
:
-
Подставим данные выражения в уравнение (1):
или
3. Значит, уравнениями (1) и (2) задаётся одна плоскость в аффинной системе координат.
II. Условие параллельности двух прямых.
Теорема 5.4.
Два
уравнения
и
в аффинной системе координат определяют
две параллельные плоскости, если
коэффициенты при переменных
в уравнениях пропорциональны.
III. Условие пересечения двух прямых.
Теорема 5.5.
Два
уравнения
и
в аффинной системе координат определяют
две пересекающие плоскости, если
коэффициенты при переменных
в уравнениях не пропорциональны.
Взаимное расположение
плоскостей
и
определяется и рангами расширенной и
основной матриц, соответствующих системе
уравнений данных плоскостей:
Пусть:
-
- расширенная
матрица ранга
-
-основная
матрица ранга
.
-
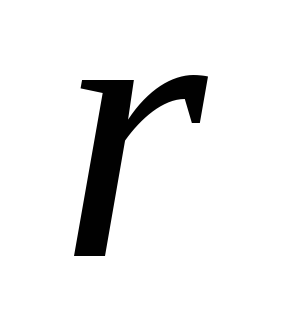Если
,
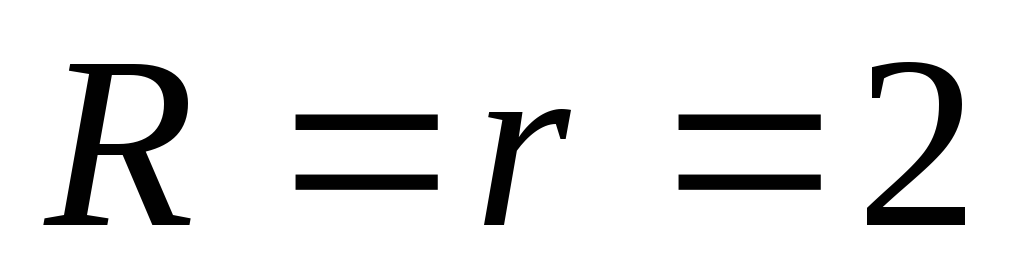то плоскости
и
пересекаются; -
Если
,
то плоскости
и
совпадают; -
Если
,
то плоскости
и
параллельны.
Пучок плоскостей.
Определение 5.6. Пучком плоскостей называется совокупность плоскостей пространства, проходящих через одну прямую.
Пусть плоскости
и
пересекаются, причем
:
;
:
Помножим уравнения
плоскостей
и
соответственно на числа
и q,одновременно
не равные 0, и сложим полученные равенства:
(*)
,
где
Коэффициенты при х,у,z не равны нулю одновременно, т.к. одновременное равенство нулю позволяет говорить, что
.
По условию параллельности плоскостей
имеем, что
=> противоречит
условию.
Уравнение (*) есть уравнение плоскости, проходящей через общую прямую двух данных плоскостей.
—
уравнение пучка
плоскостей.
Пример.
Задача: Составить уравнение плоскости, проходящей через точку А(2,3,1) и прямую, определяемую плоскостями:х+у-2z+1=0 и 2x-y+z-4=0.
Определение 5.7. Совокупность всех плоскостей, проходящих через точку пересечения трех основных плоскостей, называются связкой плоскостей.
—уравнение
связки.
Расстояние от точки до плоскости.
З
адача:
Найти расстояние от точки
до
плоскости :
.
Решение:
1.
,
2.
3. Вектор
=>
4. Так как точка
принадлежит
плоскости, то имеем:
5.
или
- расстояние
от точки Мо до плоскости.
Расстояние между двумя параллельными плоскостями.
Задача:
Найти расстояние между параллельными
плоскостями
и
,
заданными своими уравнениями:
и
.
Угол между плоскостями.
Определение 5.8. Углом между плоскостями называется любой из двух двугранных углов, образованный этими плоскостями.
—формула
угла между
и
.